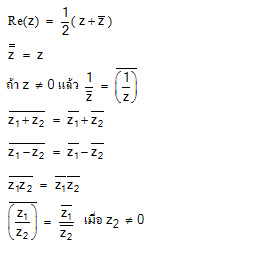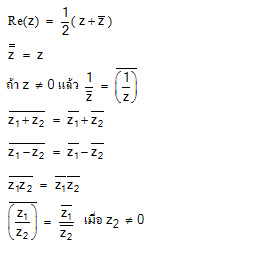จำนวนเชิงซ้อน (Complex Numbers)-การคูณจำนวนเชิงซ้อนด้วยจำนวนเชิงซ้อน และ สังยุคของจำนวนเชิงซ้อน ม.5
| กำหนดให้ |
z1 |
= |
a + bi |
|
z2 |
= |
c + di |
| จะได้ |
z1z2 |
= |
(a + bi)(c + di) |
|
|
= |
a(c + di) + (bi)(c +di) |
|
|
= |
ac + adi + bic + bidi |
|
|
= |
ac + adi + bci + bdi2 |
|
|
= |
ac + adi + bci + bd(-1) |
|
|
= |
ac – bd + adi + bci |
|
|
= |
(ac – bd) + (adi + bci) |
| ดังนั้น |
z1z2 |
= |
(ac – bd) + (ad + bc)i |
|
|
|
และ |
z2 |
= |
c + di |
|
จะได้ว่า |
z1z2 |
= |
(ac – bd) + (ad + bc)i |
|
|
|
|
จงหาค่าของ (4 + 3i)(5 + 6i) |
|
|
วิธีที่ 1 ใช้สูตร |
|
|
|
|
|
(4 + 3i)(5 + 6i) |
= |
[(4)(5) – (3)(6)] + [(4)(6) + (3)(5)]i |
|
|
|
|
|
= |
(20 – 18) + (24 + 15)i |
|
|
|
|
|
= |
2 + 39i |
|
|
|
วิธีที่ 2 ใช้วิธีคูณกระจาย |
|
|
|
|
|
(4 + 3i)(5 + 6i) |
= |
(4)(5) + (4)(6i) + (3i)(5) + (3i)(6i) |
|
|
|
|
|
= |
20 + 24i + 15i + 18i2 |
|
|
|
|
|
= |
20 + 24i + 15i + 18(-1) |
|
|
|
|
|
= |
20 + 39i – 18 |
|
|
|
|
|
= |
2 + 39i |
|
|
|
|
|
จงหาค่าของ (3 + 2i)(3 – 2i) |
|
|
วิธีที่ 1 ใช้สูตร |
|
|
|
|
|
(3 + 2i)(3 – 2i) |
= |
[(3)(3) – (2)(-2)] + [(3)(-2) + (2)(3)]i |
|
|
|
|
|
= |
(9 + 4) + (-6 + 6)i |
|
|
|
|
|
= |
13 + 0i |
|
|
|
|
|
= |
13 |
|
|
|
วิธีที่ 2 ใช้วิธีคูณกระจาย |
|
|
|
|
|
(3 + 2i)(3 – 2i) |
= |
(3)(3) + (3)(-2i) + (2i)(3) + (2i)(-2i) |
|
|
|
|
|
= |
9 – 6i + 6i + (-4)i2 |
|
|
|
|
|
= |
9 + (-4)(-1) |
|
|
|
|
|
= |
9 + 4 |
|
|
|
|
|
= |
13 |
|
|
|
|
|
กำหนดให้ z1 = 2 + 3i, z2 = 6 + i, z3 = -2i และ z4 = -1 – 4i จงหาค่าของ |
|
| 1. 2(z1 + z2) |
2. 3z1 + 4z3 |
3. 3z1z4 – 4z2 |
4. |
|
|
|
|
1. |
2(z1 + z2) |
= |
2[(2 + 3i) + (6 + i)] |
|
|
|
|
|
= |
2[(2 + 6) + (3 + 1)i] |
|
|
|
|
|
= |
2(8 + 4i) |
|
|
|
|
|
= |
16 + 8i |
|
|
|
2. |
3z1 + 4z3 |
= |
3(2 + 3i) + 4(-2i) |
|
|
|
|
|
= |
6 + 9i – 8i |
|
|
|
|
|
= |
6 + i |
|
|
|
3. |
3z1z4 – 4z2 |
= |
3[(2 + 3i)(-1 – 4i)] – 4(6 + i) |
|
|
|
|
|
= |
3[(2)(-1) + 2(-4i) + (3i)(-1) + (3i)(-4i)] – 24 – 4i |
|
|
|
|
|
= |
3[-2 – 8i – 3i – 12i2] – 24 – 4i |
|
|
|
|
|
= |
3[-2 – 11i – 12(-1)] – 24 – 4i |
|
|
|
|
|
= |
3[-2 – 11i + 12] – 24 – 4i |
|
|
|
|
|
= |
3(10 – 11i) – 24 – 4i |
|
|
|
|
|
= |
30 – 33i – 24 – 4i |
|
|
|
|
|
= |
6 – 37i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| สังยุค (conjugate) ของ z เขียนแทนด้วย |
 |
|
|
โดยที่ |
z |
= |
a – bi |
|
|
|
สังยุคของจำนวนเชิงซ้อน
ในทางคณิตศาสตร์ สังยุคของจำนวนเชิงซ้อน (complex conjugate) เปรียบได้กับการเปลี่ยนเครื่องหมายบนส่วนจินตภาพของจำนวนเชิงซ้อนนั้นให้เป็นตรงข้าม เช่น กำหนดให้จำนวนเชิงซ้อน z = a + ib ดังนั้นสังยุคของ z คือ
z = a − ib (เมื่อ a กับ b แทนจำนวนจริง)
การบ่งบอกว่าจำนวนเชิงซ้อนใดเป็นสังยุค ให้เขียนขีดเส้นตรงไว้เหนือจำนวนเชิงซ้อน หรือใส่เครื่องหมายดอกจัน (*) ไว้ที่มุมขวาบน เช่น z* แต่ในที่นี้จะใช้ขีดเพื่อไม่ให้สับสนกับสัญลักษณ์ของการสลับเปลี่ยนสังยุค (conjugate transpose) ของเมทริกซ์ ดังตัวอย่าง
แนวความคิดอีกอย่างหนึ่งคือการให้จำนวนเชิงซ้อนเป็นพิกัดอยู่บนระนาบในระบบพิกัดคาร์ทีเซียน โดยให้แกน x เป็นส่วนจริงและแกน y เป็นสัมประสิทธิ์ของ i (ส่วนจินตภาพ) ในแผนภาพทางขวามือ พิกัดของจำนวนเชิงซ้อนสังยุคเปรียบเหมือนภาพสะท้อนที่อยู่บนแกน x
สำหรับฟังก์ชัน 
ที่เป็นฟังก์ชันฮอโลมอร์ฟิก (holomorphic function) และ 
มีการนิยามไว้แล้ว จะได้
|
สังยุคของ |
2 + 3i |
คือ |
2 -3i |
|
|
สังยุคของ |
-6 + 4i |
คือ |
-6 – 4i |
|
|
สังยุคของ |
3 – 2i |
คือ |
3 + 2i |
|
|
สังยุคของ |
-5 – i |
คือ |
-5 + i |
|
|
สังยุคของ |
6i |
คือ |
-6i |
|
|
สังยุคของ |
-2i |
คือ |
2i |
|
|
สังยุคของ |
7 |
คือ |
7 |
|
|
สังยุคของ |
3 |
คือ |
3 |
|
สมบัติกำหนดให้ z, z1 และ z2 เป็นจำนวนเชิงซ้อน จะได้ว่า
