การทดลองสุ่ม (random experiment)
การทดลองสุ่ม (random experiment) คือ การทดลองหรือการกระทำใด ๆ ซึ่งทราบว่าผลลัพธ์อาจจะเป็นอะไรได้บ้าง แต่ไม่สามารถบอกได้อย่างถูกต้องแน่นอนว่า ในแต่ละครั้งที่ทดลองผลที่เกิดขึ้นจะเป็นอะไรในบรรดาผลลัพธ์ที่อาจเป็นไปได้เหล่านี้
ตัวอย่างที่ 1 จงพิจารณาว่าการกระทำต่อไปนี้ เป็นการทดลองสุ่มหรือไม่ เพราะเหตุใด
1) การโยนเหรียญ 1 เหรียญ หนึ่งครั้ง
ตอบ เป็นการทดลองสุ่ม เพราะว่าในการโยนเหรียญ 1 เหรียญ หนึ่งครั้ง อาจจะออกหัวหรือก้อย แต่ไม่สามารถระบุได้แน่นอนว่าจะออกหัวหรือก้อย
2) การทอดลูกเต๋า 1 ลูก หนึ่งครั้งลงในถ้วย
ตอบ เป็นการทดลองสุ่ม เพราะว่าในการทอดลูกเต๋า 1 ลูก หนึ่งครั้งลงในถ้วย ลูกเต๋าจะหงายหน้าที่มีแต้ม 1, 2, 3, 4, 5 และ 6 แต่ไม่สามารถระบุได้แน่นอนว่าลูกเต๋าจะหงายหน้าที่มีแต้มใด
3) การเดินทางไปโรงเรียน
ตอบ ไม่เป็นการทดลองสุ่ม เพราะว่าในการเดินทางไปโรงเรียน เราไม่สามารถตอบได้เลยว่าผลลัพธ์เป็นอะไรบ้าง
4) การแข่งขันฟุตบอลในแต่ละนัด
ตอบ เป็นการทดลองสุ่ม เพราะว่าในการแข่งขันฟุตบอลในแต่ละนัด มีผล แพ้ ชนะ หรือ เสมอ แต่ไม่สามารถระบุได้แน่นอนว่าผลการแข่งขันจะเป็นแบบใด
5) การถอนเงินจากธนาคาร
ตอบ ไม่เป็นการทดลองสุ่ม เพราะว่าในการถอนเงินจากธนาคาร เราไม่สามารถตอบได้เลยว่าผลลัพธ์เป็นอะไรบ้าง
จากตัวอย่างข้างต้น สรุปได้ว่า
เราไม่สามารถบอกล่วงหน้าได้ว่าผลลัพธ์ที่เกิดขึ้น จากแต่ละการกระทำจะเป็นอะไร แต่สามารถบอกได้ว่ามีผลลัพธ์อะไรบ้างที่จะเกิดขึ้นได้ เรียกการกระทำเหล่านี้ว่า การทดลองสุ่ม
ปริภูมิตัวอย่าง
ปริภูมิตัวอย่าง หรือแซมเปิลสเปซ (S) คือ เซตของผลลัพธ์ที่อาจจะเกิดขึ้นทั้งหมดจากการทดลองสุ่ม
ตัวอย่างที่ 3 จงเขียนแซมเปิลสเปซ และหาจำนวนของผลลัพธ์ทั้งหมดที่เป็นไปได้ จากการทดลองสุ่มต่อไปนี้
1) การโยนเหรียญเที่ยงตรง 1 เหรียญ 2 ครั้ง
ตอบ แซมเปิลสเปซที่เป็นไปได้ทั้งหมด ได้แก่ HH, HT, TH, TT
จำนวนของแซมเปิลสเปซหรือผลลัพธ์ทั้งหมดที่เป็นไปได้ เท่ากับ 4
2) สุ่มหยิบลูกปิงปอง 2 ลูกพร้อมกัน จากกล่องใบหนึ่ง ที่มีลูกปิงปอง สีม่วง 1 ลูก, สีส้ม 1 ลูก และสีเขียว 1 ลูก
ตอบ แซมเปิลสเปซที่เป็นไปได้ทั้งหมด ได้แก่ ม่วงส้ม, ม่วงเขียว และส้มเขียว
จำนวนของแซมเปิลสเปซหรือผลลัพธ์ทั้งหมดที่เป็นไปได้ เท่ากับ 3
ตัวอย่างที่ 4 มีแป้นวงกลมอยู่หนึ่งแป้นได้จาการแบ่งวงกลม ออกเป็น 10 ส่วน มีหมายเลขกำกับ 0,1,2,3,4,5,6,7,8,9 ตามลำดับ หมุนแป้น 1 ครั้ง ให้นักเรียนตอบคำถามต่อไปนี้
-
- ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ เป็นอย่างไร
ตอบ มี 10 แบบ คือ 0,1,2,3,4,5,6,7,8,9
-
- ผลลัพธ์ที่เข็มชี้ในช่องจำนวนคู่ เป็นอย่างไร
ตอบ มี 5 แบบ คือ 0,2,4,6,8
-
- ผลลัพธ์ที่เข็มชี้ในช่องจำนวนคี่ เป็นอย่างไร
ตอบ มี 5 แบบ คือ 1,3,5,7,9
-
- ผลลัพธ์ที่เข็มชี้ในช่องมากกว่า 7 เป็นอย่างไร
ตอบ มี 2 แบบ คือ 8,9
-
- ผลลัพธ์ที่เข็มชี้ในช่องเป็นจำนวนเฉพาะ เป็นอย่างไร
ตอบ มี 4 แบบ คือ 2,3,5,7
- การทดลองสุ่ม ( random experiment ) คือการทดลองที่ไม่สามารถทำนายผลลัพธ์ได้อย่างถูกต้อง
ตัวอย่าง การโยนเหรียญขึ้นไปในอากาศ ถือว่าเป็นการทดลองสุ่ม เพราะยังไม่ทราบว่าเหรียญจะหงายหัวหรือก้อย
การทอดลูกเต๋า 1 ลูก ถือว่าเป็นการทดลองสุ่ม เพราะยังไม่ทราบว่าลูกเต๋าจะขึ้นแต้ม 1 , 2 , 3 , 4 , 5 หรือ 6
- แซมเปิลสเปซ ( sample space ) คือเซตของผลลัพธ์ที่อาจเป็นไปได้ทั้งหมดของการทดลองสุ่ม
ตัวอย่าง เช่น ในการโยนเหรียญ 2 อัน 1 ครั้ง ถ้ามีผลลัพธ์ที่เราสนใจคือ การขึ้นหัวหรือก้อย
จะได้แซมเปิลสเปซ คือ {(H,H), (H,T), (T,H), (T,T)} เมื่อ (H,T) หมายถึงเหรียญอันที่ 1 ขึ้นหัว และเหรียญอันที่ 2 ขึ้นก้อย
- ในการโยนเหรียญ 2 อัน 1 ครั้ง ถ้ามีผลลัพธ์ที่เราสนใจคือ จำนวนก้อยที่ขึ้น จะได้แซมเปิลสเปซ คือ { 0 , 1 , 2 }
- เมื่อ 0 หมายถึงไม่ขึ้นก้อยทั้ง 2 อัน (นั่นคือขึ้นหัวทั้งสองอัน)
- 1 หมายถึงขึ้นก้อยเพียง 1 อัน (ขึ้นหัว 1 อัน)
- 2 หมายถึงขึ้นก้อยทั้ง 2 อัน
- เหตุการณ์ ( event ) คือสับเซตของแซมเปิลสเปซ
ความน่าจะเป็น ของเหตุการณ์
- คือ โอกาสที่จะเกิดเหตุการณ์ที่สนใจเท่ากับเท่าใด
หลักการหาความน่าจะเป็น
- ให้ S เป็นแซมเปิลสเปซ ซึ่งแต่ละผลลัพธ์ใน S มีโอกาสเกิดขึ้นเท่าๆกัน E เป็นสับเซตของ S
- ให้ P(E) เป็นสัญลักษณ์แทน ความน่าจะเป็นของเหตุการณ์ E เราสามารถหา P(E) ได้ดังนี้
ตัวอย่าง กล่องใบหนึ่งมีลูกแก้วสีขาว 3 ลูก สีแดง 2 ลูก หยิบลูกแก้วจากกล่อง 2 ลูก
- จงหาเหตุการณ์ที่จะได้ลูกแก้วสีขาว 1 ลูก สีแดง 1 ลูก
- เนื่องจากเราสนใจแซมเปิลสเปซของลูกแก้วแต่ละลูกที่ถูกหยิบขึ้นมา
- ดังนั้นเราให้ ข1 , ข2 , ข3 เป็นลูกแก้วสีขาว 3 ลูก และ ด1 , ด2 เป็นลูกแก้วสีแดง 2 ลูก
- แซมเปิลสเปซ S = { ข1ข2 ,ข1ข3 , ข1ด1 ,ข1ด2, ข2ข3 , ข2ด1 , ข2ด2 , ข3ด1 , ข3ด2 , ด1ด2 }
- ให้ A เป็นเหตุการณ์ที่ผลลัพธ์เป็นลูกแก้วสีขาว 1 ลูก และสีแดง 1 ลูก
- เหตุการณ์ A = { ข1ด1 , ข1ด2 , ข2ด1 , ข2ด2 , ข3ด1, ข3ด2 }
-
- กฎสำคัญบางประการของความน่าจะเป็น
ให้ A เป็นเหตุการณ์ใดๆ และ S เป็นแซมเปิลสเปซ สมบัติความน่าจะเป็นของ A ดังนี้
1. 0 P (A) 1
2. ถ้า A = { } แล้ว P (A) = 0 นั่นคือ P ( { } ) = 0
3. ถ้า A = S แล้ว P (A) = 1 นั่นคือ P(S) = 1
สมบัติของความน่าจะเป็นของเหตุการณ์ 2 เหตุการณ์
ให้ A และ B เป็นเหตุการณ์ 2 เหตุการณ์ ใน S แซมเปิลสเปซ
1. P (A U B) = P (A) + P (B) – P (A ∩B)
2. P (A U B) = P (A) + P (B) เมื่อ A ∩B = { }
3. P (A) = 1 – P (A’)
4. P (A-B) = P (A) – P (A∩B)
ตัวอย่าง กำหนดให้ P (A) = 0.6 P (B’) = 0.4 และ P (A – B) = 0.2 จงหา P (A ‘ ∩B’)
จาก P (B’) = 0.4
จะได้ว่า P (B) = 1 – P (B’) = 1 – 0.4 = 0.6
จาก P (A) = 0.6 และ P (A – B) = 0.2
เนื่องจาก P (A) = P (A – B) + P (A ∩B)
(ถ้านักเรียนไม่เข้าใจให้เขียนแผนภาพทางด้านเซตดู)
0.6 = 0.2 + P (A ∩ B)
P (A ∩B) = 0.4
เนื่องจาก P (A’ ∩ B’) = P (A U B)’
= 1 – P (A U B)
จากสมบัติความน่าจะเป็น P (A’ ∩B’) = 1 – [P (A) + P (B) – P (A ∩B)]
= 1 – [0.6 + 0.6 – 0.4] = 1 – 0.8 = 0.2
ความน่าจะเป็นแบบเงื่อนไข
บางครั้งเราทราบว่าเหตุการณ์หนึ่งเกิดขึ้น เราต้องการหาความน่าจะเป็นที่อีกเหตุการณ์หนึ่งเกิดขึ้น เรียกความน่าจะเป็นแบบนี้ว่า ความน่าจะเป็นแบบเงื่อนไข
ให้ A และ B เป็นเหตุการณ์ โดยที่ P (B) > 0 เขียน P (A/B) แทนความน่าจะเป็นของ A เมื่อกำหนดว่าเหตุการณ์ B เกิดขึ้นแล้ว
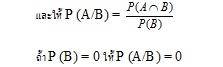
ความน่าจะเป็นของเหตุการณ์ที่เป็นอิสระต่อกัน
พิจารณาในการโยนเหรียญ 1 อัน 2 ครั้ง จะเห็นว่าการที่การโยนเหรียญครั้งหนึ่งขึ้นหัวหรือก้อย ไม่มีผลต่อการขึ้นหัวหรือก้อยในการโยนครั้งที่สอง
เรากล่าวว่าการโยนทั้งสองครั้งเป็นอิสระต่อกันนิยาม เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (A ∩B) = P (A) P (B)
ทฤษฎีบท เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (A/B) = P (A)
เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (B/A) = P (B)
ตัวอย่าง โยนลูกเต๋า 2 ลูก 2 ครั้ง จงหาความจะเป็นที่ผลรวมของแต้มแต่ละครั้งเท่ากับ 5
ให้ A แทนเหตุการณ์ที่ผลรวมของแต้มในการโยนครั้งที่ 1 เป็น 5
B แทนเหตุการณ์ที่ผลรวมของแต้มในการโยนครั้งที่ 2 เป็น 5

เนื่องจากการโยนลูกเต๋าแต่ละครั้งเป็นอิสระต่อกัน
ดังนั้นความน่าจะเป็นที่ผลรวมของแต้มแต่ละครั้งเป็น 5 เท่ากับ
P (A∩ B) = P (A) P (B)
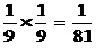
- กฎสำคัญบางประการของความน่าจะเป็น
ขอบคุณข้อมูล https://nockacademy.com/






