การนำเมทริกซ์ไปประยุกต์ใช้ในชีวิตประจำวัน

ในระดับอุดมศึกษาจึงมีการนำไปประยุกต์ใช้ในสาขาต่างๆ โดยในการเรียนวิชาพีชคณิตเชิงเส้น ได้มีการกล่าวถึงการประยุกต์ใช้ในหลากหลายสาขา ที่มีการนำสมการเชิงเส้นไปใช้ในการอธิบายปรากฏการณ์ และความสัมพันธ์ต่างๆ ดังนี้

การประยุกต์ทางธุรกิจ
การประยุกต์ทางเศรษฐศาสตร์
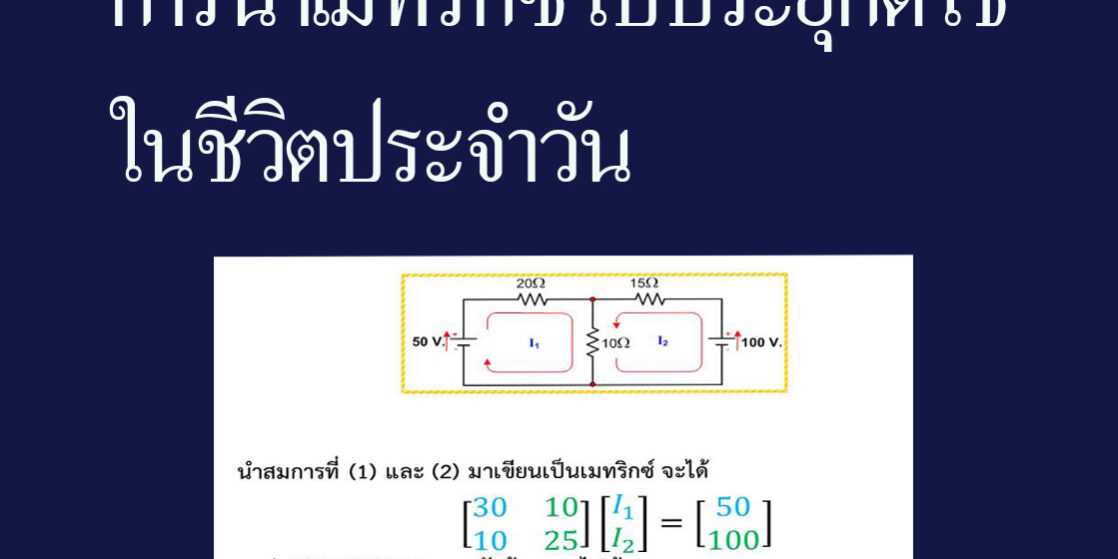
การประยุกต์ทางฟิสิกส์ (วงจรไฟฟ้า)
การวิเคราะห์การเลื่อนไหลของการจราจร

ซึ่งแต่ละประเด็นมีรายละเอียดดังต่อไปนี้

การประยุกต์ทางธุรกิจ/อุตสาหกรรม

ตัวอย่างที่ โรงงานอุตสาหกรรมแห่งหนึ่งมีเครื่องจักร 3 เครื่อง เพื่อใช้ในการผลิตสินค้าที่แตกต่างกัน 4 ชนิด เครื่องจักรแต่ละเครื่องสามารถทำงานได้วันละ 8 ชั่วโมง และจำนวนชั่วโมงที่เครื่องจักรแต่ละเครื่องในใจการผลิตสินค้าแต่ละชนิด ต่อ 1 ชิ้น กำหนดดังนี้

	ชนิดที่ 1	ชนิดที่ 2	ชนิดที่ 3	ชนิดที่ 4
เครื่องที่ 1	1	2	1	2
เครื่องที่ 2	2	0	1	1
เครื่องที่ 3	1	2	3	0

โฆษณา

REPORT THIS AD

จงหาจำนวนสินค้าแต่ละชนิดที่ผลิตได้ใน 1 วัน เมื่อกำหนดให้เครื่องจักรแต่ละตัวทำงานครบ 8 ชั่วโมง

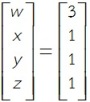
วิธีทำ สมมติให้ w แทน จำนวนสินค้าชนิดที่ 1 ที่ผลิตได้ใน 1 วัน

x แทน จำนวนสินค้าชนิดที่ 2 ที่ผลิตได้ใน 1 วัน

y แทน จำนวนสินค้าชนิดที่ 3 ที่ผลิตได้ใน 1 วัน

z แทน จำนวนสินค้าชนิดที่ 4 ที่ผลิตได้ใน 1 วัน

ดังนั้น จำนวนชั่วโมงทำงานของเครื่องจักรเครื่องที่ 1 เท่ากับ 1w + 2x + 1y + 2z

จำนวนชั่วโมงทำงานของเครื่องจักรเครื่องที่ 2 เท่ากับ 2w + 0x + 1y + 1z

จำนวนชั่วโมงทำงานของเครื่องจักรเครื่องที่ 3 เท่ากับ 1w + 2x + 3y + 0z

จากที่กำหนดให้ว่า เครื่องจักรแต่ละเครื่องทำงานวันละ 8 ชั่วโมง ดังนั้น จะได้ระบบของสมการเชิงเส้น ดังต่อไปนี้

w + 2x + y + 2z = 8

2w + y + z = 8

w + 2x + 3y = 8

การวิเคราะห์การเลื่อนไหลของการจราจร

ถ้ามีแผนผังของการจราจรในรูปแบบของการเดินรถทางเดียว พร้อมทั้งมีการสำรวจจำนวนรถที่เข้าหา หรือออกจากสี่แยก เราสามารถนำข้อมูลที่ได้มาวิเคราะห์หาจำนวนรถบนเส้นทางที่ต้องการได้ และจากคำตอบดังกล่าวนี้ หากเราทราบว่านถนนสายใดมีปัญหาที่อาจจะส่งผลถึงการจราจร เช่น การก่อสร้าง ก็อาจจะวิเคราะห์ต่อไปถึงจำนวนรถที่เหมาะสมได้

เมทริกซ์ไปประยุกต์ใช้การประยุกต์ทางฟิสิกส์ (วงจรไฟฟ้า)

การนำเมทริกซ์ไปประยุกต์ใช้ในชีวิตประจำวัน

“เมทริกซ์” เป็นเนื้อหาหนึ่งในวิชาคณิตสาสตร์เพิ่มเติม ม.4 ศึกษาเกี่ยวกับตัวแบบชนิดหนึ่งที่เรียกว่าเมทริกซ์ และมีการประยุกต์ในการแก้ระบบสมการเชิงเส้น
ในระดับอุดมศึกษาจึงมีการนำไปประยุกต์ใช้ในสาขาต่างๆ โดยในการเรียนวิชาพีชคณิตเชิงเส้น ได้มีการกล่าวถึงการประยุกต์ใช้ในหลากหลายสาขา ที่มีการนำสมการเชิงเส้นไปใช้ในการอธิบายปรากฏการณ์ และความสัมพันธ์ต่างๆ ดังนี้

การประยุกต์ทางธุรกิจ
การประยุกต์ทางเศรษฐศาสตร์
การประยุกต์ทางฟิสิกส์ (วงจรไฟฟ้า)
การวิเคราะห์การเลื่อนไหลของการจราจร

การประยุกต์ทางธุระกิจ

	ชนิดที่ 1	ชนิดที่ 2	ชนิดที่ 3	ชนิดที่ 4
เครื่องที่ 1	1	2	1	2
เครื่องที่ 2	2	0	1	1
เครื่องที่ 3	1	2	3	0

วิธีทำ สมมติให้ w แทน จำนวนสินค้าชนิดที่ 1 ที่ผลิตได้ใน 1 วัน

x แทน จำนวนสินค้าชนิดที่ 2 ที่ผลิตได้ใน 1 วัน
y แทน จำนวนสินค้าชนิดที่ 3 ที่ผลิตได้ใน 1 วัน
z แทน จำนวนสินค้าชนิดที่ 4 ที่ผลิตได้ใน 1 วัน

ดังนั้น จำนวนชั่วโมงทำงานของเครื่องจักรเครื่องที่ 1 เท่ากับ 1w + 2x + 1y + 2z
จำนวนชั่วโมงทำงานของเครื่องจักรเครื่องที่ 2 เท่ากับ 2w + 0x + 1y + 1z
จำนวนชั่วโมงทำงานของเครื่องจักรเครื่องที่ 3 เท่ากับ 1w + 2x + 3y + 0z

w + 2x +   y + 2z   =   8
2w + y + z   =   8
w + 2x + 3y =   8

ซึ่งสร้างเป็นเมทริกซ์แต่งเติมของระบบสมการเชิงเส้นได้ดังนี้

เมื่อใช้การดำเนินการตามแถวเบื้องต้นจะได้เมทริกซ์แบบขั้นบันไดแบบแถว ดังนี้

จากเมทริกซ์นี้ ทำให้เราได้ระบบสมการเชิงเส้น ดังนี้
w + 2x +   y +   z   =   4
x +    y +   z   =   2
y –   z =   0
ซึ่งจะได้คำตอบของระบบสมการดังนี้
w   =   4 – s
x   =   2 – s
y   =   s
z   =   s
เมื่อ s เป็นจำนวนใดๆ แต่เนื่องจาก w, x, y, z เป็จำนวนเต็มบวกหรือศูนย์ (จำนวนสินค้า)

ดังนั้น 4 – s ≥ 0 และ 2 – s ≥ 0
นั่นคือ s ≤ 4 และ s ≤ 2
ดังนั้น 0 £ s £ 2 จะได้ s = 0, 1, 2 แสดงว่าคำตอบของปัญหามีอยู่ 3 คำตอบ คือ

ถ้า s = 0 จะได้ หรือ

ถ้า s = 1 จะได้ หรือ

ถ้า s = 2 จะได้

แต่ถ้าระบุเงื่อนไขเพิ่มเติมอีกว่า เครื่องจักรแต่ละเครื่องต้องผลิตสินค้าได้ทุกชนิด คำตอบของปัญหานี้จะเหลือเพียงคำตอบเดียว คือ

การวิเคราะห์การเลื่อนไหลของการจราจร

ตัวอย่างสถานการณ์
ในรูปที่กำหนดให้ต่อไปนี้ แสดงเครือข่ายการจราจรบนถนนสายต่างๆ ในเมืองแห่งหนึ่ง ซึ่งเป็นถนนที่มีการเดินรถทางเดียวทั้งหมด โดยทิศทางของการเดินรถแสดงได้ด้วยลูกศรในรูป จำนวน ปรากฏในรูปแทนจำนวนรถใน 1 ชั่วโมงที่เข้าหา หรือออกจากจุดสี่แยกต่างๆ และตัวแปร x₁, x₂, …, x₇ แทนจำนวนรถใน 1 ชั่วโมงที่ผ่านจากจุด A ไปยังจุด B จากจุด B ไปยังจุด C เป็นต้น

ถ้าหากเราตั้งสมมติฐานว่า ไม่มีการหยุดการเลื่อนไหลของการจราจร จำนวนรถที่เข้าหาสี่แยกเท่ากับจำนวนรถที่ออกจากสี่แยกนั้น จงวิเคราะห์หา x₁, x₂, …, x₇
วิธีทำ
จากข้อมูลที่กำหนดให้ จะได้ระบบสมการเชิงเส้น ดังต่อไปนี้
x₁ + x₃                          =   800 (การเลื่อนไหนที่สี่แยก A)
x₁ – x₂ + x₄                 =   200 (การเลื่อนไหนที่สี่แยก B)
x₂ – x₅          =   500 (การเลื่อนไหนที่สี่แยก C)
– x₅ + x₇                       =   50    (การเลื่อนไหนที่สี่แยก D)
x₄ + x₆ – x₇                   =   600 (การเลื่อนไหนที่สี่แยก E)
x₃ + x₆          =   750 (การเลื่อนไหนที่สี่แยก F)

จะได้เมทริกซ์แต่งเติมของระบบสมการข้างต้น คือ

ซึ่งสมมูลตามแถวกับเมทริกซ์ขั้นบันไดตามแถวลดรูป ดังนี้

ดังนั้น

x₁   =   50 + x₆
x₂   =   450 + x₇
x₃   =   750 – x₆
x₄   =   600 – x₆ + x₇
x₅   =   -50 + x₇
x₆   =   x₆
x₇   =   x₇

เนื่องจาก xi ³ 0 (เพราะว่า สถานการณ์นี้เป็นการเดินรถทางเดียว ถ้าหากมี xi < 0 จะทำให้เกิดการเดินรถที่ผิดทางกัน)

ดังนั้น            x₃   =   750 – x₆  > 0
ดังนั้น            0  <  x₆  < 750
ทำนองเดียวกัน     x₅   =   -50 + x₇  > 0
x₇  > 50

ถ้าสมมติว่า ถนนที่เชื่อมระหว่างสี่แยก D และ E อยู่ใรระหว่างการก่อสร้าง จึงต้องการให้รถผ่านเส้นทางนี้น้อยที่สุด จะได้ว่า x₇ = 50 ซึ่งทำให้ x₂ = 500 และ x₅ = 0
แสดงว่า ต้องปิดการถนนที่เชื่อมระหว่างสี่แยก C และ D
ในทางกลับกัน ถ้าปิดถนนสายที่เชื่อมระหว่าง C และ D จะได้ x₅ = 0 ซึ่งทำให้ x₇ = 50 ซึ่งเป็นจำนวนที่น้อยที่สุด
ดังนั้น จึงสรุปได้ว่า จำนวนรถบนถนนที่เชื่อมระหว่าง D และ E น้อยที่สุด ก็ต่อเมื่อต้องปิดถนนสายที่เชื่อมระหว่าง C และ D
ในขณะเดียวกัน ถ้าต้องการให้ x₆ มีค่าน้อยที่สุดด้วย จาก (1) จะได้ว่า x₆ = 0
ดังนั้น x₁ = 50, x₂ = 500, x₃ = 750, x₄ = 650, x₅ = 0, x₇ = 50