การประยุกต์ของอัตราส่วนตรีโกณมิติ
การประยุกต์ของอัตราส่วนตรีโกณมิติ
การประยุกต์ของอัตราส่วนตรีโกณมิติ
ในการแก้ปัญหาเกี่ยวกับการหาระยะทางความสูง ซึ่งบางครั้งใช้เครื่องมือวัดโดยตรงไม่ได้ เช่น การวัดความสูงของภูเขา การหาความกว้างของแม่น้ำ สามารถทำได้โดยอาศัยความรู้เรื่อง อัตราส่วนตรีโกณมิติ ซึ่งจะมีขนาดของมุมเข้ามาเกี่ยวข้องรวมทั้ง มุมก้ม และ มุมเงย
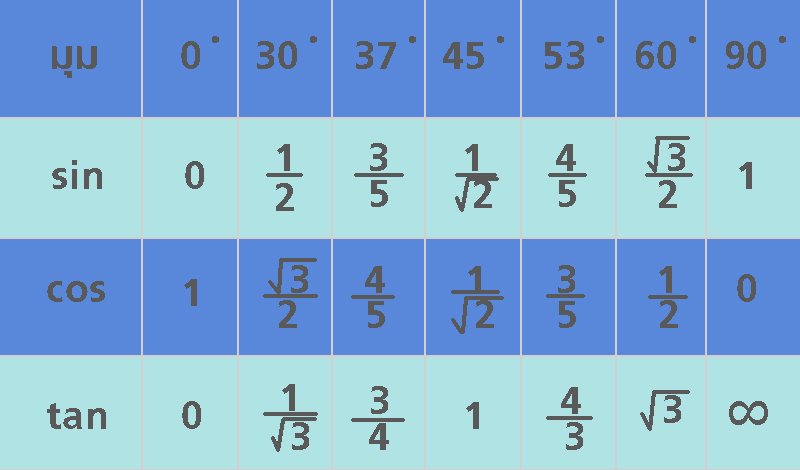
- แบมือซ้ายออกมา มองเลขมุมจับคู่กับนิ้วเรียงจากซ้ายไปขวา เป็นมุม 00, 300, 450, 900 องศา
- เมื่อต้องการหาค่าตรีโกณมิติของมุมใดให้งอนิ้วนั้น สมมติว่าหา cos 300 ก็จะตรงกับนิ้วชี้ ก็งอนิ้วชี้เก็บไว้
- ถือกฎว่า sin–ซ้าย (ออกเสียงคล้ายกัน) cos–ขวา (ออกเสียง /k/ เหมือนกัน) เมื่อหาค่าของฟังก์ชันใดให้สนใจจำนวนนิ้วมือฝั่งที่สอดคล้องกับฟังก์ชันนั้น
ตัวอย่างการหา sin30º และ cos45º
โดยใช้เทคนิคมือซ้ายที่ใช้ข้างต้น
การหาค่า sin30º
ให้พับนิ้วชี้มือซ้ายลง
พิจารณาว่าด้านซ้ายของนิ้วที่พับลงมีนิ้วอยู่กี่นิ้ว (จะได้ว่ามี 1 นิ้ว)
นำจำนวนที่ได้มาใส่ใน / (กรณฑ์ที่ 2)
จะได้ว่า sin 30º = √1/2 = 1/2
อัตราส่วนตรีโกณมิติต่างๆที่นำมาประยุกต์ใช้
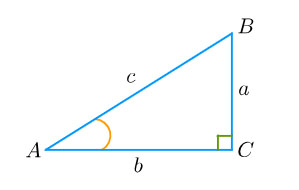
อัตราส่วนตรีโกณมิติ เป็นพื้นฐานที่สำคัญในการประยุกต์ใช้ฟังก์ชัน ตรีโกณ ม.5
sin(A) = ข้าม / ฉาก = a / c
cos(A) = ชิด / ฉาก = b / c
tan(A) = ข้าม / ชิด = a /b
cosec(A) = ฉาก / ข้าม = c / a
sec(A) = ฉาก / ชิด = c / b
cot(A) = ชิด / ข้าม = b /a
สมบัติตรีโกณมิติที่ควรทราบ
- sin2θ + cos2θ = 1
- tan2θ + 1 = sec2θ
- cot2θ + 1 = cosec2θ
- sin(A) = 1/cosec(A) และ cosec(A) = 1/sin(A)
- cos(A) = 1/sec(A) และ sec(A) = 1/cos(A)
- tan(A) = 1/cot(A) = sin(A)/cos(A) และ cot(A) = 1/tan(A) = cos(A)/sin(A)
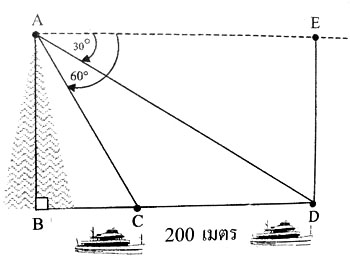
ให้ A เป็นตำแหน่งที่นักท่องเที่ยวยืน
AB แทนความสูงของประภาคาร
C แทนเรือลำที่หนึ่ง
D แทนเรือลำที่สอง
EA´D = 30″
EA´C = 60
CD = 200 เมตร







