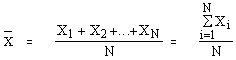การวัดค่ากลางของข้อมูล – การวิเคราะห์ข้อมูลเบื้องต้น

การวัดค่ากลางของข้อมูล

การวัดค่ากลางของข้อมูล

การหาค่ากลางของข้อมูลที่เป็นตัวแทนของข้อมูลทั้งหมดเพื่อความสะดวกในการสรุปเรื่องราวเกี่ยวกับข้อมูลนั้นๆ จะช่วยทำให้เกิดการวิเคราะห์ข้อมูลถูกต้องดีขึ้น การหาค่ากลางของข้อมูลมีวิธีหาหลายวิธี แต่ละวิธีมีข้อดีและข้อเสีย และมีความเหมาะสมในการนำไปใช้ไม่เหมือนกัน ขึ้นอยู่กับลักษณะข้อมูลและวัตถุประสงค์ของผู้ใช้ข้อมูลนั้นๆ

ค่ากลางของข้อมูลที่สำคัญ มี 3 ชนิด คือ

1.        ค่าเฉลี่ยเลขคณิต (Arithmetic mean)

2.       มัธยฐาน (Median)

3.       ฐานนิยม (Mode)

 1.   ค่าเฉลี่ยเลขคณิต (Arithmetic mean)
ใช้สัญลักษณ์ คือ

1.1 การหาค่าเฉลี่ยเลขคณิตของข้อมูลที่ไม่แจกแจงความถี่

ให้ x 1 , x 2 , x 3 , …, x N เป็นข้อมูล N ค่า x̄

1.ค่าเฉลี่ยเลขคณิต (arithmetic mean)

          n    คือ จำนวนข้อมูลทั้งหมด

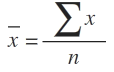
ค่าเฉลี่ยเลขคณิต หรือที่เราเรียกกันย่อๆ ว่าค่าเฉลี่ย เขียนแทนด้วยสัญลักษณ์ (x¯) เป็นค่ากลางทางสถิติค่าหนึ่ง ที่เจอบ่อยและใช้กันเยอะมาก

 

วิธีการหาค่าเฉลี่ยเลขคณิตของข้อมูลแบบไม่แจกแจงความถี่สามารถทำได้ดังนี้

ตัวอย่าง 1 )  หาค่าเฉลี่ยจากข้อมูลชุดนี้ 1,2,2,5,7,11,15,9

วิธีทำ

 

ตอบ 6.5

 

คุณสมบัติบางประการของมัชฌิมเลขคณิต

 

มัชฌิมเลขคณิตมีคุณสมบัติบางประการดังนี้ประการแรก คุณสมบัติพื้นฐานก็คือ ผลบวกของความเบี่ยงเบนของคะแนนดิบกับคะแนนเฉลี่ยมีค่าเป็น 0ค่ามัชฌิมเลขคณิตของคะแนน 7, 13, 22, 9, 11 และ 4 คือ 11 ส่วนเบี่ยงเบนจากคะแนนเฉลี่ยคือ -4, 2, 11, -2, 0 และ -7 ผลบวกของคะแนนเบี่ยงเบนคือ 0 ผลทั้งหมดเขียนเป็นสัญลักษณ์ได้ดังนี้

ประการสอง ผลรวมของกำลังสองของคะแนนเบี่ยงเบนจะมีค่าน้อยที่สุดความเบี่ยงเบนของค่าที่ได้จากการวัด 7, 13, 22, 9, 11, 4 กับค่าเฉลี่ย 11 คือ -4, 2, 11, -2, 0, -7 ค่ากำลังสองของความเบี่ยงเบนจะได้ 16, 4, 121, 4, 0, 49 ผลบวกของกำลังสองเท่ากับ 197 ถ้าหากเราใช้ค่าเฉลี่ยตัวอื่น ๆ ผลบวกของกำลังสองของความเบี่ยงเบนของค่าการวัดกับค่ากึ่งกลางใด ๆ จะได้ค่าสูงกว่าผลรวมของกำลังสองความเบี่ยงเบนของค่าการวัดกับมัชฌิมเลขคณิต สมมติให้ค่ากึ่งกลางของข้อมูลชุดนี้เป็น 13 ความเบี่ยงเบนจะได้ -6, 0, 9, 4, 2, -9 ยกกำลังสองได้ 36, 0, 81, 16, 4, 81 รวมผลทั้งหมดเท่ากับ 218 ซึ่งมากกว่าค่าที่ได้จากการใช้ค่าเฉลี่ย

ข้อดีข้อเสียของมัชฌิมเลขคณิต

ข้อดี

1. คำนวณได้ง่าย

2. ข้อมูลทุกตัวถูกนำมาใช้ในการคำนวณ

3. สามารถนำค่าเฉลี่ยที่ได้มาใช้ในการคำนวณอื่น ๆ

ข้อเสีย

1. เพราะข้อมูลทุกค่าถูกนำมาใช้ในการคำนวณ ถ้ามีข้อมูลบางค่าผิดปกติค่าเฉลี่ยก็จะผิดปกติไปด้วย

2. ในกรณีที่อันตรภาคชั้นแต่ละชั้นเป็นชั้นเปิด ไม่สามารถหามัชฌิมเลขคณิตได้

2.มัธยฐาน (Median)

มัธยฐาน หมายถึงค่าที่อยู่ในตำแหน่งกึ่งกลางของข้อมูลชุดนั้น เมื่อได้จากเรียงค่าของข้อมูลจากน้อยที่ไปหามากที่สุดไปหาน้อยที่สุด ค่ากึ่งกลางจะเป็นตัวแทนที่แสดงว่ามีข้อมูลที่มากกว่าและน้อยกว่านี้อยู่ 50 เปอร์เซนต์

การหาค่ามัธยฐานของข้อมูลที่ไม่ได้จัดหมวดหมู่(Ungrouped Data)

ให้เรียงข้อมูลที่มีค่าน้อยที่สุดไปหาข้อมูลที่มีค่ามากที่สุดหรือจากมากสุดไปหาน้อยที่สุดแล้วหาคะแนนที่อยู่ในตำแหน่งกึ่งกลาง

จงหามัธยฐานของข้อมูลต่อไปนี้ 9,5,11,16,6,10,13,14,3

    วิธีทำ    เรียงข้อมูลที่มีค่าน้อยที่สุดไปหาข้อมูลที่มีค่ามากที่สุดคือ

                3,5,6,9,10,11,13,14,16

                Median จะอยู่ตำแหน่งที่  N+1   =  9+1

                                                                     2          2        = 5

 ดังนั้น ค่ามัธฐานเท่ากับ 10

 การหาค่ามัธยฐานของข้อมูลที่จัดหน่วยหมู่(Grouped Data)

 จากข้อมูลในตารางแจกแจงความถถี่ จงหาค่ามัธยฐาน

คะแนน	ความถี่
5-9	3
10-14	4
15-19	3
20-24	7
25-29	6
30-39	4
35-39	2
40-44	3
N = 32

วิธีทำ

1.  หาความถี่สะสม

2.  หาตำแหน่งของมัธยฐาน

คะแนน	ความถี่	ความถี่สะสม
5-9	3	3
10-14	4	7
15-19	3	10
20-24	7	17
25-29	6	23
30-34	4	27
35-39	2	29
40-44	3	32
N=32

(N)

  2     =  16 ค่ามัธยฐานที่อยู่ในชั้น 20-24

  L = 19.5

 I = 5

F = 10

f =  7

แทนค่า Mdn = 19.5 + 5(16-10) = 19.5 – 4.2 = 23.7 ดังนั้น มัธยฐานคือ 23.7

3.ฐานนิยม (Mode)

     ฐานนิยม หมายถึงค่าของค่าคะแนนที่ซ้ำกันมากที่สุดหรือค่าคะแนนที่มีความถี่สูงที่สุดในข้อมูลชุดนั้นจงหาฐานนิยมของข้อมูลต่อไปนี้ 3,2,4,5,6,4,8,4,7,10

วิธีทำ ข้อมูลที่ชั้นกันมากที่สุดคือ 4  ดังนั้น ฐานนิยมคือ 4 ข้อมูลบางชุดอาจมีฐานนิยมได้มากกว่า 1 ค่า เซ่น 10. 14, 12, 10, 11, 13, 12 14 12 10 ข้อมูลที่ชั้ากันมากที่สุดคือ 10 กับ 12 ดังนั้นฐานนิยม คือ 10 กับ 12 ข้อมูลบางชุดอาจจะไม่มีฐานนิยมซึ่ง ได้แก่ ข้อมูลที่มีรายการซํ้าจำนวนเท่ากันหลายชุค 1ช่น 5, 2, 3, 4, 7, 8, 2, 3, 5, 9, 10, 2, 3, 5, 7, 9, 8, 7, 8 ข้อมูลที่ไม่มีรายการซํ้ากันเลย เช่น’8, 9, 10, 11, 13, 15