การวิเคราะห์ข้อมูลและความน่าจะเป็น (Probability)
ในทางสถิติ คาว่า “การทดลอง (Experiment)” หมายถึงกระบวนการในการที่จะก่อให้เกิดชุด ของข้อมูล ชุดของข้อมูลในที่นี้หมายถึงผลทั้งหมดที่เป็นไปได้ที่เกิดขึ้นจากการทดลอง ตัวอย่างเช่นใน การทดลองโยนเหรียญ 1 เหรียญ ผลที่เกิดขึ้นเป็นไปได้ 2 แบบด้วยกันคือ หัวหรือก้อย ในการทดลอง โยนลูกเต๋า 1 ลูก ผลที่เกิดขึ้นก็จะเป็นไปตามแต้มของลูกเต๋า ผลของการทดลองที่ออกมาแตกต่างกัน นั้น สะท้อนให้เห็นถึงความหมายของคาว่า “ความไม่แน่นอน (Uncertainty)” ความน่าสนใจจะอยู่ที่ การศึกษาโอกาส(Chance)หรือความนา่จะเป็นของการที่จะเกิดผลเป็นแบบใดแบบหนึ่งว่าเป็นเท่าใด
สเปซตัวอย่าง(SampleSpace)
เซตของผลที่เป็นได้ทั้งหมดจากการทดลองจะเรียกว่า สเปซตัวอย่าง และเขียนแทนด้วยเซต S ผลของการทดลองแต่ละแบบเรียกว่าเป็นสมาชิก (Element) หรือจุดตัวอย่าง (Sample Point)
ในการโยนลูกเต๋า 1 ลูก ถ้าสนใจแต้มบนลูกเต๋า จะได้ S = {1,2,3,4,5,6}
แต่ถ้า สนใจว่าเป็นแต้มคู่หรือคี่ จะได้ S = {ค,ู่คี}่
ในการทดลองทาข้อสอบปรนัย 3 ข้อ ถ้าสนใจว่าทาถูกหรือผิด จะได้ S = {TTT, TTF, TFT, FTT, FFT, FTF, TFF, FFF} โดยที่ T หมายถึงทาข้อสอบถูก และ F หมายถึงทาข้อสอบผิด
แต่ถ้าสนใจจำนวนข้อที่ทาถูก จะได้ S = {0,1,2,3}
ข้อสังเกตจะเห็นได้ว่าในการทดลองหนงึ่ๆสเปซตัวอย่างอาจมีได้หลายแบบทั้งนี้ขึ้นอยู่กับความ สนใจผลของการทดลองว่าเป็นแบบใด
เหตุการณ์ (Events)
นิยาม เหตุการณ์ หมายถึง เซตย่อย (Subset) ของสเปซตัวอย่าง ตัวอย่างเช่น ในการโยนลูกเต๋า 1 ลูก
นิยาม กำหนดสเปซตัวอย่าง S และกาหนดเหตุการณ์ A คอมพลีเมนต์ (Complement) ของ เหตุการณ์ A เขียนแทนด้วย A’ หมายถึง เซตของสมาชิกของ S ที่ไม่ได้เป็นสมาชิกของเหตุการณ์ A
นิยาม กาหนดสเปซตัวอย่าง S และกาหนดเหตุการณ์ A และ B ยูเนียน (Union) ของเหตุการณ์ A และ B เขียนแทนด้วย A B หมายถึงเซตของสมาชิกS ที่อยู่ใน A หรือ B
นิยาม กาหนดสเปซตัวอย่าง S และกาหนดเหตุการณ์ A และ B อินเตอร์เซคชัน (Intersection) ของ เหตุการณ์ A และ B เขียนแทนด้วย A B หมายถึงเซตของสมาชิก S ที่อยู่ใน A และ B
ตัวอย่าง กล่องใบหนึ่งมีสลากที่มีหมายเลขตั้งแต่ 1 – 20 อย่างละ 1 ใบ ถ้าหยิบสลาก 1 ใบจากกล่อง ใบนี้ จะได้ว่า S = {1, 2, 3,…, 20}
ถ้า A เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 2 ลงตัว B เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 3 ลงตัว
จะได้ว่า A = {2,4,6,8,10,12,14,16,18,20}
B = {3,6,9,12,15,18}
A’ = เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 2 ไม่ลงตัว
A’ = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
A B = เป็นเหตุการที่สลากนั้นมีหมายเลขที่หารด้วย 2 หรือ 3 ลงตัว
A B = {2, 3, 4, 6, 8, 9, 10, 12, 14, 16, 18, 20}
A B = เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 2 และ 3 ลงตัว
A B = {6,12,18}
นิยาม 8.6 เหตุการณ์ A และ B จะถูกเรียกว่าเป็นเหตุการณ์ที่ไม่เกิดร่วมกัน (Mutually Exclusive Events) ถ้าAB=
ตัวอย่างเช่น จากตัวอย่างที่หยิบสลากที่ได้กล่าวข้างต้น ถ้าให้
C เป็นเหตุการณ์ที่สลากมีหมายเลขหารด้วย 5 ลงตัว
D เป็นเหตุการณ์ที่สลากมีหมายเลขหารด้วย7ลงตัว
C = {5,10,15,20}
D = {7,14}
ในที่นี้ C D = ดังนั้นเหตุการณ์ C และ D เรียกว่าเป็นเหตุการณ์ที่ไม่เกิดร่วมกัน
การนับจุดตัวอย่าง
สิ่งที่สาคัญในการทดลองสถิติก็คือ จุดตัวอย่างที่เป็นไปได้ทั้งหมดเป็นอะไรได้บ้าง และมี จานวนเท่าใด โดยเฉพาะอย่างยิ่งจานวนของจุดตัวอย่าง จะเป็นสิ่งสาคัญในการคานวณหาโอกาสที่จะ เกิดขึ้นของเหตุการณ์ต่างๆ หลักการที่สาคัญอันหนึ่งในการนับจานวนจุดตัวอย่างที่เป็นไปได้ก็คือ กฎ การคูณ (Multiplication Rule)
ทฤษฎีบท ถ้างานหนึ่งสามารถเลือกทาได้ใน n1 วิธี และในแต่ละวิธีของ n1 สามารถเลือกทางาน อย่างที่สองได้ใน n2 วิธี ดังนั้นจานวนวิธีที่จะทางานทั้งสองงานเท่ากับ n1n2 วิธี
ตัวอย่าง ชายคนหนึ่งมีเสื้อเชิ้ตอยู่ 5 ตัว และกางเกงอยู่ 4 ตัว อยากทราบว่าชายคนนี้จะแต่งตัวได้ ทั้งหมดกี่วิธี
วิธีทา ชายคนนี้เลือกใส่เสื้อได้5วิธี
และหลังจากใส่เสื้อแล้ว ชายคนนั้นเลือกใส่กางเกงได้อีก 4 วิธี
ดังนั้น จานวนวิธีที่เขาจะแต่งตัวได้ทั้งหมดเท่ากับ 5 4 = 20 วิธี
ตัวอย่าง ในการโยนเหรียญ 2 เหรียญ จานวนจุดตัวอย่างที่เป็นไปได้ทั้งหมดมีกี่แบบ วิธีทา ในการโยนเหรียญที่ 1 เหตุการณ์ที่เป็นไปได้คือเหรียญขึ้น หัวหรือก้อยซึ่งมี 2 แบบ
ในการโยนเหรียญที่ 2 ก็เช่นกัน เป็นไปได้อีก 2 แบบ ดังนั้นจานวนจุดตัวอย่างที่เป็นไปได้ในการโยนเหรียญ 2 เหรียญคือ 2 2 = 4 แบบ
ทฤษฎีบท ถ้ามีงานที่ต้องทา k อย่าง ทั้งนี้งานที่ 1 มีทางเลือก n1 วิธี งานที่ 2 มีทางเลือก n2 วิธี … งานที่ k มีทางเลือก nk วิธี ดังนั้นในการทางาน k อย่างนั้น สามารถทาได้ทั้งหมด n 1 n 2 n 3 …n k วิธี
ตัวอย่าง ในการสร้างเลข 4 หลักจากเลข 0, 1, 2, 3, 4, 5 ถ้าแต่ละหลักสามารถใช้เลขซ้ากันได้ อยาก ทราบว่าเลข 4 หลักที่เป็นไปได้นั้นมีทั้งหมดกี่จานวนที่เป็นเลขคี่
วิธีทำ
ตัวอย่าง
วิธีทำ
การเรียงสิ่งของที่แตกต่างกัน n สิ่ง ในแนวเส้นตรง
นิยาม การจัดลาดับ (Permutation) คือการจัดเรียงลาดับของสิ่งของจานวนหนึ่ง ซึ่งอาจจะเป็น สิ่งของทั้งหมดหรือเป็นเพียงบางส่วน
ตัวอย่าง 8.5 ถ้านาอักษร 4 ตัว a, b, c และ d มาเรียงลาดับกัน จะได้ทั้งหมดกี่วิธี
วิธีทำ ถ้าพิจารณาอักษร 4 ตัวมาเรียงกันในลักษณะ _ _ _ _
1 2 3 4
จะเห็นได้ว่าในตาแหน่งที่ 1 สามารถเลือกตัวอักษรดังกล่าวได้ 4 วิธี หลังจากเลือกตัวอักษรที่ตาแหน่งที่ 1 แล้วเหลือตัวอักษรที่จะอยู่ตาแหน่งที่ 2 ได้ 3 วิธี และ หลังจากเลือกตัวอักษรตาแหน่งที่ 2 จะเหลือตัวอักษรที่จะอยู่ในตาแหน่งที่ 3 และ 4 ได้ 2 วิธี และ 1 วิธี ตามลาดับ
ดังนั้นการนาอักษร 4 ตัวมาเรียงลาดับกันจะได้ = 4 3 2 1 วิธี
= 4!วิธี
= 24วิธี
ทฤษฎี การจัดลาดับสิ่งของ n สิ่งที่แตกต่างกันจะได้ n! วิธี
ตัวอย่าง 8.6 ถ้านำคน 5 คนมายืนเรียงกันจะได้ทั้งหมดกี่วิธี
วิธีทำ การนาคน 5 คนมาเรียงกันจะได้ = 5! วิธี
= 120วิธี
การเรียงสิ่งของที่แตกต่างกัน r สิ่งจากของทั้งหมด n สิ่ง
ในการจัดลาดับสิ่งของนั้น บางครั้งอาจไม่ได้นามาเรียงกันทั้งหมด กล่าวคอื ถ้ามีสิ่งของ ทั้งหมด n สิ่ง อาจจะนามาเรียงลาดับกันเพยี ง r ส่ิง โดยที่ r < n
ถ้าสิ่งของ n สิ่งที่แตกต่างกันนำมาเรียงกันทีละ r สิ่งจะเป็นในลักษณะดังน้ี _ _ _ … _
1 2 3 r
จะเห็นได้ว่าในตาแหนง่ ที่ 1 สามารถเลอื กสิง่ ของได้ n วธิ ี
ในตาแหน่งท่ี 2 สามารถเลือกสงิ่ ของได้ n – 1 วธิ ี
ในตาแหนง่ ที่ 3 สามารถเลอื กสงิ่ ของได้ n – 2 วธิ ี
…
ในตาแหน่งที่ n สามารถเลอื กสิง่ ของได้ n – (n – 1) วธิ ี
ดังนนั้ จานวนวธิ ที ีเ่ รียงส่ิงของ r สง่ิ จาก n สิ่ง = n (n – 1)(n – 2)…(n – (r –1)) วธิ ี
= n! /(nr)! วิธี
ทฤษฎี การจัดลาดับของ n สง่ิ ท่ีแตกตา่ งกัน แตน่ ามาเรียงกนั r สงิ่ จะได้จานวนวิธีทง้ั หมดเท่ากับ
n P r = n! /(nr)! วิธี
ตัวอย่าง จากอักษร a, b, c, d และ e นามาเรียงกันเพียง 3 ตัว จะได้กี่วิธี
วิธีทำ จำนวนวิธีที่จะเรียงอักษร 3 ตัวจาก 5 ตัวนั้นจะได้ = 5!/(5-3)!
= 60 วิธี
ตัวอย่าง หนังสือที่แตกต่างกัน 6 เล่ม ถ้านหนังสือเพียงแค่ 2 เล่มมาเรียงกัน จะได้ทั้งหมดกี่วิธี
วิธีทำ หนังสอื 6 เล่มเอามาเรียงกัน 2 เล่มจะได้ทั้งหมด = 6! /(6-2)! วิธี
= 30 วิธี
การเรียงสิ่งของที่แตกต่างกัน n สิ่งในแนววงกลม
ในการนำของ n สิ่งที่แตกต่างกันมาเรียงกันในแนวเส้นตรงนั้น จานวนวิธีที่ได้เท่ากับ n! วิธี อย่างเช่นการเอาตัวอักษร a, b, c มาเรียงกันจะได้ทั้งหมด 3! วิธี ซึ่งได้แก่ abc, acb, bac, bca, cab และ cba ถ้าทั้ง 6 แบบดังกล่าวมาเรียงในแนววงกลมจะเป็นดังนี้
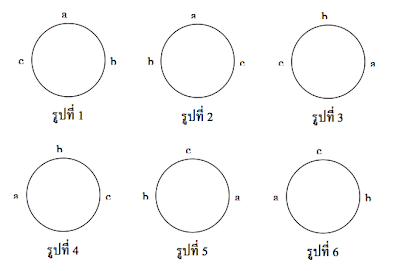
ทฤษฎี ถ้ามีของ n สิ่งที่แตกต่างกัน นามาเรียงกันเป็นวงกลม จะได้ทั้งหมด (n – 1)! วิธี
ตัวอย่าง ถ้าคน 5 คนมายืนเรียงกันเป็นวงกลมจะได้กี่วิธี
วิธีทำ จานวนวิธีที่คน 5 คนมายืนเรียงกันเป็นวงกลม = (5 – 1)! วิธี
การเรียงสิ่งของ n สิ่งแต่มีบางสิ่งที่ซ้้ากัน
ในการเรียงตวัอักษร6ตัวคือa1,a2,a3,b1,b2,cสลบักันไปมานัน้จะได้ท้ังหมด6!แบบ ด้วยกัน ทั้งนี้ใน 6!แบบนั้นมีที่ตัว อักษรa1,a2และa3สลบักันไปมา3!แบบซงึ่ถ้าคดิว่าตัวอกัษรa1, a และ a นั้นเหมือนกันคือเป็น a ตัวเดียวกัน จานวนแบบทจี่ ะได้ก็จะลดลงเหลือ 6!/3! แบบ และในทำนองเดียวกัน สาหรบั ตวั อักษร b1 และ b2 ซ่ึงถ้าคิดวา่ เปน็ b เหมือนกนั จานวนแบบทั้งหมดที่เป็นไปได้ก็จะะเท่ากับ 6!/3!2! แบบ
ทฤษฎี ในการเรียงลาดับสิ่งของ n สิ่ง ซึ่งใน n สิ่งนี้มีสิ่งของ n1 สิ่งทซี่ ้ากัน มีสง่ิ ของ n2 ส่งิ ทีซ่ า้ กนั …และสิ่งของnk สิ่งที่ซ้ำกันจะได้ว่าการเรียงลาดับสิ่งของnสิ่งนั้นเท่ากับ n! /n !n !…n ! 12k วิธี
ตัวอย่าง จากตัวอักษรในคำว่า “STATISTICS” ถ้านำมาเรียงกันไปมาโดยไม่สนใจความหมายจะ ได้ท้ังหมดกี่วิธิี
วิธีทำ จากตัวอักษรในคาดังกล่าว จะมี “S” 3 ตัว “T” 3 ตัว “I” 2 ตัว และ “A” และ “C” อย่างละ 1 ตัว
ดังนน้ั จานวนวธิ ีที่ตัวอกั ษรในคาดังกลา่ ว เรียงสลับกันจะได้ = 10! /3! 3! 2! 1! 1! วิธี
= 50,400 วิธี
กฎที่สำคัญต่างๆ
ในการคานวณหาความน่าจะเป็นของเหตุการณ์หนึ่งๆนั้น อาจหาได้ง่ายขึ้นถ้าทราบกฎบางข้อ ที่เกี่ยวข้องกับการหาความน่าจะเป็นดังกล่าวนั้น
ทฤษฎี กำหนดสเปซตัวอย่าง S และกาหนดเหตุการณ์ A และ B จะได้ว่า P(A B) = P(A) + P(B) – P(A B)
ทฤษฎี กำหนดสเปซตัวอย่าง S และกาหนดเหตุการณ์ A และ B วา่ เป็นเหตุการณ์ที่ไม่เกิด ร่วมกัน จะได้ว่า P(A B) = P(A) + P(B)
ทฤษฎี กำหนดสเปซตัวอย่าง S และกาหนดเหตุการณ์ A จะได้ว่า P(A) + P(A) = 1
ตัวอย่าง กล่องใบหนึ่งมีสลากที่มีหมายเลข1-30อย่างละใบหยิบสลาก1ใบจากกล่องใบนี้จง หาความน่าจะเป็นที่
- สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย 3 ลงตัว
- สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย 3 ไม่ลงตัว
- สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย5ลงตัว
- สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย 3 และ 5 ลงตัว
- สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย 3 หรือ 5 ลงตัว
วิธีทำ 1.ให้ A เป็นเหตุการณ์ที่สลากที่หยิบได้เป็นสลากที่มหี มายเลขที่หารด้วย 3 ลงตัว
ในที่นี้ A = {3, 6, 9, …, 27, 30}
จะได้ว่า P(A) = 10/30 = 1/3
2. ให้ A’ เป็นเหตุการณ์ที่สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย 3 ไม่ลงตัว
จาก P(A’) = 1–P(A)
= 1- 1/3 = 2/3
3. ให้ B เป็นเหตุการณ์ที่สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารด้วย 5 ลงตัว
ในที่นี้ B = {5, 10, 15, 20, 25, 30}
จะได้ว่า P(B) = 6/30 = 1/5
4. AB จะเป็นเหตุการณ์ที่สลากที่หยิบได้เป็นสลากทมี่ีหมายเลขที่หารด้วย3และ5ลงตัว
ในที่นี้ AB)= {15,30}
จะได้ว่า P(AB) = 2/30 = 1/15
5. ABเป็นเหตุการณ์ที่สลากที่หยิบได้เป็นสลากที่มีหมายเลขที่หารดว้ย3หรือ5ลงตัว
จาก P(A B) = P(A) + P(B) – P(A B)
จะได้ว่า P(AB) = 10/30 + 6/30 – 2/30
= 14/30 = 7/15






