การหารลงตัว (Divisibetity)-ทฤษฎีจำนวนเบื้องต้นคณิตออนไลน์

ทฤษฎีจำนวนเบื้องต้น

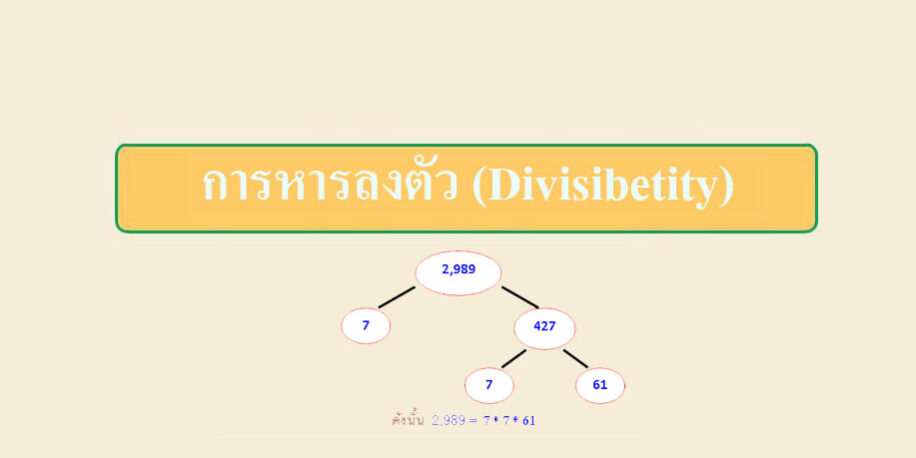
การหารลงตัว (Divisibetity)

บทนิยาม ให้ a และ b เป็นจำนวนเต็ม โดยที่ a 0 เรากล่าวว่า
a หาร b ลงตัว ก็ต่อเมื่อ มีจำนวนเต็ม c ที่ทำให้

b = ac

จะเรียก a ว่าเป็น ตัวหาร (divisor)

และเรียก b ว่าเป็นพหุคูณ (multiple) ของ b

ถ้า a หาร b ลงตัว แทนด้วย a | b

และถ้า a หาร b ไม่ลงตัว แทนด้วย a b

ตัวอย่างที่ 1 กล่าวอธิบายความคิด การหารลงตัว เช่น

13 | 182 เพราะ 182 = 13·14

-5 | 30 เพราะ 30 = (-5)(-6)

6 44 เพราะ ไม่มีจำนวนเต็ม c ที่ทำให้ 44 = b(c)

ตัวอย่างที่ 2 จำนวนเต็มที่หาร 6 ลงตัว ได้แก่ +1, +2, +3 และ +6
จำนวนเต็มที่หาร 17 ลงตัว ได้แก่ +1 และ +17

ทฤษฎีบทการหารลงตัว

ทฤษฎีบท 1 การถ่ายทอด
ถ้า a, b และ c เป็นจำนวนเต็ม ซึ่ง a | b และ b | c และ a | c

ตัวอย่างที่ 3 จากทฤษฎีบท
11 | 66 และ 66 | 198 บอกให้เราทราบว่า 11 | 198

ทฤษฎีบท 2 ถ้า a และ b เป็นจำนวนเต็ม ซึ่ง a | b แล้ว | a || b |

ทฤษฎีบท 3 ทฤษฎีผลรวมเชิงเส้น (linear combination)
ถ้า a, b และ c เป็นจำนวนเดิม โดยที่ a | b และ a | c แล้ว
a | (bx+cy) เมื่อ x และ y เป็นจำนวนเต็มใด ๆ
นำความรู้เรื่องการหารลงตัวไปใช้แบ่งจำนวนเต็มเป็นจำนวนเฉพาะ และจำนวนประกอบ

บทนิยาม จำนวนเต็มบวก p เป็นจำนวนเฉพาะ ก็ต่อเมื่อ p1
และถ้าจำนวนเต็ม x หาร p ลงตัว แล้ว x{1, -1, p, -p}

หมายเหตุ จำนวนเต็มบวกอื่น ๆ ที่ไม่ใช่ 1 และไม่ใช่จำนวนเฉพาะ เรียกว่า
จำนวนประกอบ (composite Number)

ทฤษฎีบท 4 ทฤษฎีบท หลักมูลทางเลขคณิต (The Fundamental Theosur of Asuthmetic) กล่าวว่า
จำนวนเต็มบวกทุกจำนวนที่มากกว่า 1 สามารถเขียนได้ในรูปผลคูณของจำนวนเฉพาะได้
เพียงแบบเดียวเท่านั้น ทั้งนี้ไม่รวมการสลับที่ตัวคูณ หรือการคูณด้วย 1

เช่น 3750 = 2 X 3 X 54
500 = 22 X 30 X 58

ข้อสังเกต