การอ้างเหตุผล ตรรกศาสตร์ ม.4
คือ การอ้างว่า สำหรับเหตุการณ์ P1, P2,…, Pn ชุดหนึ่ง สามารถสรุปผลที่ตามมา C ได้ โดยการอ้างเหตุผลประกอบด้วย 2 ส่วน คือ เหตุ (สิ่งที่กำหนดให้) และ ผล (สิ่งที่ตามมา)
สำหรับการพิจารณาว่า การอ้างเหตุผลนั้นสมเหตุสมผลหรือไม่ สามารถพิจารณาได้จากประพจน์ ( P1 ∧ P2 ∧ … Pn) → C ถ้าประพจน์ดังกล่าวมีค่าความจริงเป็นจริงเสมอ (เป็นสัจนิรันดร์) เราสามารถสรุปได้ว่าการอ้างเหตุผลดังกล่าวเป็นการอ้างที่สมเหตุสมผล
ตัวบ่งปริมาณ (∀,∃) และ การอ้างเหตุผลตรรกศาสตร์เบื้องต้น
ประโยคเปิด (Open Sentence) คือ ข้อความที่อยู่ในรูปประโยคบอกเล่าหรือปฏิเสธ ที่มีตัวแปรและสื่อแทนค่าของตัวแปรนั้น จะได้ค่าความจริงแน่นอน หรือเป็นประพจน์ นิยมใช้สัญลักษณ์ P(x), P(x , y), Q(x , y) แทนประโยคเปิดที่มีตัวแปรระบุในวงเล็บ
ตัวบ่งปริมาณ (∀,∃)
คือ ตัวระบุจำนวนสมาชิกในเอกภพสัมพัทธ์ที่ทำให้ประโยคเปิดกลายเป็นประพจน์ ตัวบ่งปริมาณมี 2 ชนิด คือ
- ตัวบ่งปริมาณที่กล่าวถึงสมาชิกทุกตัวในเอกภพสัมพัทธ์ ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ ∀ อ่านว่า “สำหรับสมาชิก x ทุกตัว”
- ตัวบ่งปริมาณที่กล่าวถึงสมาชิกบางตัวในเอกภพสัมพัทธ์ ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ ∃ อ่านว่า “สำหรับสมาชิก x บางตัว”
ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ
- ∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง
- ∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ
- ∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง
- ∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง
นิเสธของประพจน์ที่มีตัวบ่งปริมาณ
- ~∀x[P(x)] สมมูลกับ ∃x[~P(x)]
- ~∃x[P(x)] สมมูลกับ∀x[~P(x)]
- ~∀x[~P(x)] สมมูลกับ∃x[P(x)]
- ~∃x[~P(x)] สมมูลกับ∀x[P(x)]
การอ้างเหตุผลตรรกศาสตร์เบื้องต้น
2 การอ้างเหตุผล (Argument)
การอ้างเหตุผลในเชิงตรรกวิทยาหมายถึงกระบวนการการคิดของมนุษย์ที่เรียบเรียงข้อเท็จจริง ข้อความ
ประโยคบางส่วน หรือปรากฏการณ์ต่างๆ ที่สามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จมาสนับสนุนกันและกัน จนทำให้
เกิดข้อความใหม่หรือปรากฏการณ์ใหม่ที่สามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จ การอ้างเหตุผลจะประกอบด้วย
ข้อความ 2 กลุ่ม ได้แก่
– ข้ออ้าง (Premises) : กลุ่มของข้อความ ประโยค ปรากฏการณ์ที่สนับสนุนกันและกัน
– ข้อสรุป (Conclusion) : กลุ่มของข้อความใหม่หรือปรากฏการณ์ใหม่ที่ได้มากจากข้ออ้าง
การอ้างเหตุผลในเชิงตรรกวิทยานั้นสามารถแบ่งลักษณะการอ้างเหตุผลได้เป็น 2 ลักษณะ ดังนี

การอ้างเหตุผลจะสมเหตุสมผล ก็ต่อเมื่อ ถ้าข้ออ้างเป็นจริงแล้วผลสรุปเป็นจริงด้วย
นอกจากกรณีนี้เราจะกล่าวว่า การอ้างเหตุผลดังกล่าวไม่สมเหตุสมผล
การอ้างเหตุผลเชิงนิรนัย (Deductive Argument) เป็นกระบวนการอ้างเหตุผลที่ข้ออ้างสามารถ
ยืนยันข้อสรุปได้อย่างชัดเจน ความน่าเชื่อถือของข้อสรุปอยู่ในขั้นความแน่นอน
ตัวอย่าง 1 เหตุ 1. นักศึกษาที่เล่นกีฬาทุกคนจะต้องมีสุขภาพดี
2. ก้อยเป็นนักศึกษาและชอบเล่นกีฬา
ผล ก้อยมีสุขภาพดี
วิธีทำ พิจารณาโดยการก าหนดเซตของสิ่งต่างๆ ดังนี้
กำหนดให้ A เป็นเซตของนักศึกษา B เป็นเซตของคนที่เล่นกีฬา C เป็นเซตของคนที่มีสุขภาพดี และ x แทนก้อย
จากเหตุที่กำหนดให้ สามารถแสดงได้ดังภาพ
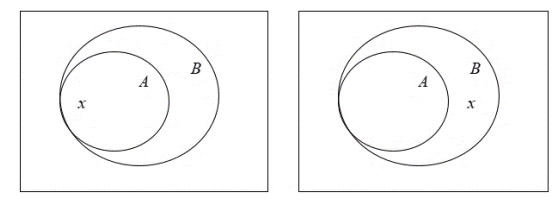
จะเห็นได้ว่า x อยู่ในเซต A หรือ x
ไม่อยู่ในเซต A ก็ได้เราสามารถสรุปได้ทั้งสองกรณี
กรณีที่ 1 : เป็ดเป็นเครื่องบินเครื่องบินชนิดหนึ่ง กรณีที่ 2 : เป็ดไม่เป็นเครื่องบินชนิดหนึ่ง
ดังนั้นจากข้อสรุปทั้ง 2 กรณี ท าให้ได้ว่าการอ้างเหตุผลดังกล่าวไม่สมเหตุสมผล
ตัวอย่าง 3 เหตุ 1. พนาวัลย์เป็นคนไทย 2. คนไทยบางคนชอบเลี้ยงช้าง
3. คนชอบเลี้ยงช้างบางคนชอบเลี้ยงแมว
ผล พนาวัลย์ชอบเลี้ยงแมว
วิธีท า พิจารณาโดยการก าหนดเซตของสิ่งต่างๆ ดังนี้
กำหนดให้ A
เป็นเซตของคนไทย, B
เป็นเซตของคนชอบเลี้ยงช้าง, C เป็นเซตของคนชอบเลี้ยงแมว, และ x แทนพนาวัลย์
จากเหตุที่กำหนดให้ สามารถแสดงได้ดังภาพ
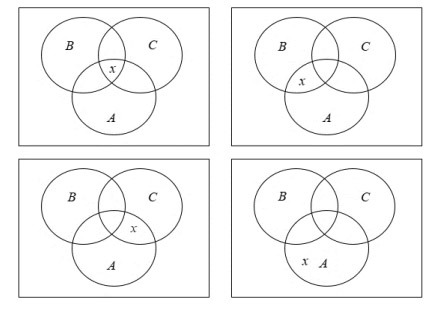
จะเห็นได้ว่า xอยู่ในเซต A ∩ B ∩ C
หรือ x อยู่ในเซตn A ∩ B
หรือ x อยู่ในเซต A ∩ C
หรือ x อยู่ในเซต A
เพียงอย่างเดียว เราสามารถสรุปได้ถึง 4 กรณี
กรณีที่ 1 : พนาวัลย์เป็นคนไทยที่ชอบเลี้ยงแมวและช้าง
กรณีที่ 2 : พนาวัลย์เป็นคนไทยชอบเลี้ยงช้าง
กรณีที่ 3 : พนาวัลย์เป็นคนไทยชอบเลี้ยงแมว
กรณีที่ 4 : พนาวัลย์เป็นคนไทยที่ไม่ชอบเลี้ยงแมวและช้าง
ดังนั้นจากข้อสรุปทั้ง 4 กรณี ท าให้ได้ว่าการอ้างเหตุผลดังกล่าวไม่สมเหตุสมผล
2. การอ้างเหตุผลเชิงอุปนัย (Inductive Argument) เป็นกระบวนการอ้างเหตุผลที่เกิดจากการสังเกต
ทดลองหลายๆ ครั้งแล้วน ามาเป็นข้อสรุป ดังนั้นข้อสรุปของการอ้างเหตุผลแบบอุปนัยนั้น ไม่จ าเป็นต้องถูกทุกครั้ง
สัญลักษณ์ทางตรรกศาสตร์ (Logic Symbols)
เนื่องจากเราทราบกันดีว่าวิชาตรรกศาสตร์นั้นเป็นวิชาที่ว่าด้วยการอ้างเหตุผลเพื่อให้เกิดข้อสรุป การอ้างเหตุผลนั้นในชีวิตจริงมักไม่ได้มีเพียงแค่หนึ่งเหตุ แต่มักจะมีเหตุที่ซับซ้อนกันหลายๆ เหตุเพื่อให้ได้มาซึ่ง
ข้อสรุป ดังนั้นการสื่อความหมายเพื่อให้เข้าใจตรงกัน ชัดเจน รัดกุม และถูกต้อง จึงจ าเป็นต้องอาศัย “สัญลักษณ์” มาใช้แทนข้อความที่มีความหมายในเชิงตรรกวิทยา สัญลักษณ์ดังกล่าวเราเรียกว่า “สัญลักษณ์ทางตรรกศาสตร์” นั้นเอง
1.3.1 ประพจน์ (Proposition)
ประพจน์ คือ ประโยคหรือข้อความที่สามารถบอกได้ว่ามีค่าความจริง เป็นจริง หรือเป็นเท็จ เพียงอย่างใด อย่างหนึ่งเท่านั้น ส่วนประโยคที่มีลักษณะเป็น ประโยคบอกเล่า, ค าถาม, ค าสั่ง, ขอร้อง, อุทาน ฯลฯ ที่ไม่สามารถ บอกได้ว่ามีค่าความจริง เป็นจริงหรือเป็นเท็จ อย่างใดอย่างหนึ่งได้ ประโยคเหล่านี้เราจะถือว่าไม่เป็นประพจน์
ตัวอย่าง ประโยคที่เป็นประพจน์
หนึ่งวันมี 24 ชั่วโมง ค่าความจริงเป็นจริง
19 < 12 ค่าความจริงเป็นเท็จ
ดวงอาทิตย์ขึ้นทางทิศตะวันออก ค่าความจริงเป็นจริง เดือนที่ลงท้ายด้วย “ยน” มี 31 วัน ค่าความจริงเป็นเท็จ






