การเคลื่อนที่แนวตรง วิชาฟิสิกส์ ม.4
การเคลื่อนที่แนวตรง
1. ปริมาณการเคลื่อนที่ (Quantities of motion)
2. สูตรการเคลื่อนที่( Formulas of Rectilinear )
3. การเคลื่อนที่แบบเส้นตรงในแนวดิ่งหรือดิ่งเสรี (Free fall)
4. กราฟการเคลื่อนที่เเนวเส้นตรง (Rectilinear motion Graphical Interpretation)
1. ปริมาณการเคลื่อนที่ (Quantities of motion)
ความหมายของการเคลื่อนที่
– การเคลื่อนที่ (Motion) หมายถึง ขบวนการอย่างหนึ่งที่ทำให้มีการเปลี่ยนแปลงตำแหน่งอย่างต่อเนื่องตามเวลาที่ผ่านไป โดยมีทิศทางและระยะทาง
– การเคลื่อนที่ในแนวเส้นตรง (Rectilinear motion) หมายถึง การเคลื่อนที่ของวัตถุที่เป็นแนวเส้นตรงซึ่งความสัมพันธ์ระหว่างความเร็ว เวลา ความเร่ง และระยะทางที่วัตถุเคลื่อนที่ไปได้ (นันทพงษ์ ลายทอง และคณะ, 2549) ลักษณะการเคลื่อนที่ในแนวเส้นตรง สิ่งต่าง ๆ ที่อยู่รอบตัวซึ่งมีการเคลื่อนที่นั้นจะมีการเคลื่อนที่แตกต่างกันออกไป เช่น การเคลื่อนที่ในแนวตรง แนวโค้ง เป็นวงกลม หรือกลับไปกลับมาในการที่เราจะพิจารณาว่าวัตถุมีการเคลื่อนที่หรือไม่ พิจารณาที่ มีการเปลี่ยนตำแหน่งหรือไม่ ถ้ามีการเปลี่ยนตำแหน่ง ถือเป็นการเคลื่อนที่
– การบอกตำแหน่งของวัตถุ การบอกตำแหน่งของสิ่งต่าง ๆ นั้นทำได้โดยการบอกตำแหน่งเทียบกับตำแหน่งหรือสิ่งที่สังเกตได้โดยง่าย ซึ่งเรียกว่า ตำแหน่งอ้างอิงหรือจุดอ้างอิง ซึ่งต้องเป็นจุดที่หยุดนิ่ง
ในชีวิตประจำวัน เราพบเห็นการเคลื่อนที่ของสิ่งต่างๆ เช่น นกบิน รถยนต์แล่นบนถนน ลูกฟุตบอลเคลื่อนที่ในอากาศ ใบพัดลมหมุน เด็กแกว่งชิงช้า ผลไม้หล่นจากต้น เป็นต้น การเคลื่อนที่ดังกล่าวมีลักษณะเฉพาะอย่างไร และขึ้นกับปัจจัยอะไรบ้าง นักเรียนจะได้ศึกษาต่อไป
ความหมายของการเคลื่อนที่
การเคลื่อนที่ (Motion) หมายถึง ขบวนการอย่างหนึ่งที่ทำให้มีการเปลี่ยนแปลงตำแหน่งอย่างต่อเนื่องตามเวลาที่ผ่านไปโดยมีทิศทางและระยะทาง
การเคลื่อนที่ในแนวเส้นตรง
การเคลื่อนที่แนวตรง เป็นการเคลื่อนที่ของวัตถุจากตำแหน่งหนึ่งไปสู่อีกตำแหน่งหนึ่ง มีแนวทางการเคลื่อนที่เป็นเส้นตรง ได้แก่ การเคลื่อนที่ของรถบนรางตรง การตกของวัตถุ ภายใต้แรงดึงดูดของโลก ในการเปลี่ยนตำแหน่งหรือการเคลื่อนที่ของวัตถุย่อมเกี่ยวข้องกับปริมาณต่าง ๆ เช่น ระยะทาง การกระจัด อัตราเร็ว ความเร็ว และความเร่ง เป็นปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แนวตรง
ปริมาณที่เกี่ยวข้อง
ความเร่ง (Acceleration)
| ชนิดของปริมาณ | หน่วย | |
| สเกลาร์ | เวกเตอร์ | |
| ระยะทาง (Distance) | การกระจัด (Displacement) | เมตร (m) |
| อัตราเร็ว (Speed) | ความเร็ว (Velocity) | เมตรต่อวินาที (m/s) |
| อัตราเร่ง (Acceleration) | ความเร่ง (Acceleration) | เมตรต่อวินาที2 (m/s2) |
จากตารางสรุปจะเห็นได้ว่าปริมาณที่เกี่ยวข้องกับการเคลื่อนที่จะมีทั้งปริมาณที่เป็นเวกเตอร์และสเกลาร์
2. สูตรการเคลื่อนที่( Formulas of Rectilinear )
สูตร 4 สูตร ด้านบน เป็นสมการการเคลื่อนที่แนวเส้นตรงแบบมีความเร่ง (a)
ความเร่ง หมายถึง การเปลี่ยนแปลงความเร็วในหนึ่งหน่วยเวลา เริ่มงงแล้วใช่ไหม?
เอาง่ายๆ ถ้าเราขับรถด้วยความเร็ว 80 km/hr จากกรุงเทพไปเชียงใหม่ ขับ 80 ตลอดทาง
เจอไฟแดงก็ขับ 80 ไฟเขียวก็ขับ 80 ไอ้แบบนี้ไม่มีความเร่ง (a=0) เพราะความเร็วมันคงที่ที่ 80
แต่ถ้าจะเปลี่ยนความเร็วเป็น 120 km/hr สิ่งแรกที่ต้องทำคือ เร่งเครื่องใช่ไหม? นั่นแหละพอความเร็วเปลี่ยน มันก็คือมีความเร่ง
ดังนั้นความเร่งก็คือ การเปลี่ยนแปลงความเร็ว/ เวลา ความเร็วเปลี่ยนมากก็เร่งมาก ความเร็วเปลี่ยนน้อยก็เร่งน้อย
เป็นอันว่ารู้จักความเร่งกันแล้วนะ
กลับมาที่ 4 สูตรด้านบน ถ้าสมมุติให้วัตถุเคลื่อนที่ด้วยความเร็วคงที่ (a=0)
สูตรที่ 1 ได้ v = u
สูตรที่ 2 ได้ s = vt ; [(2v)/2]t หรือ [(2u)/2]t โดยที่ v=u ก็ความเร็วมันคงที่นี่! อย่าลืม
สูตรที่ 3 ได้ s=ut หรือ s=vt โดยที่ v=u ก็ความเร็วมันคงที่นี่! อย่าลืม
สูตรที่ 4 ได้ v^2 = u^2 หรือ v = u
3. การเคลื่อนที่แบบเส้นตรงในแนวดิ่งหรือดิ่งเสรี (Free fall)
การตกอย่างเสรี (Free Falling) เป็นการเคลื่อนที่ในแนวดิ่งภายใต้ความโน้มถ่วงของโลก หรือเป็นการเคลื่อนที่อย่างอิสระของวัตถุ โดยมีความเร่งคงที่เท่ากับ ความเร่งเนื่องจากแรงดึงดูดของโลก ( g ) มีทิศทางพุ่งลงสู่จุดศูนย์กลางของโลกมีค่าประมาณ 9.8 หรือ 10 เมตร/วินาที2
การศึกษาการตกอย่างเสรีในที่นี้เราจะกล่าวถึงลักษณะของการเคลื่อนที่ 3 ลักษณะ ได้แก่
1. ปล่อยวัตถุลงในแนวดิ่งด้วยความเร็วต้นเท่ากับศูนย์
2. ปาลงในแนวดิ่งด้วยความเร็วต้น
3. ปาขึ้นในแนวดิ่งด้วยความเร็วต้น
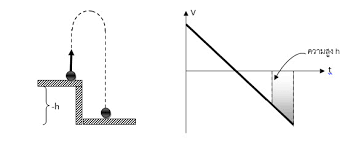
สมการสำหรับการคำนวณ
การเคลื่อนที่ของวัตถุในแนวดิ่งจะใช้สมการในการคำนวณเหมือนกับการเคลื่อนที่ใน แนวเส้นตรง แต่เปลี่ยนความเร่งของวัตถุที่เคลื่อนที่ในแนวดิ่งเป็น ความเร่งเนื่องจากแรงดึงดูดของโลก ( ![]() ) ดังนั้นสามารถเขียนสมการการเคลื่อนที่ในแนวดิ่งได้ดังนี้
) ดังนั้นสามารถเขียนสมการการเคลื่อนที่ในแนวดิ่งได้ดังนี้
1. ![]() ใช้เมื่อโจทย์ไม่กำหนด s
ใช้เมื่อโจทย์ไม่กำหนด s
2. 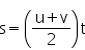 ใช้เมื่อโจทย์ไม่กำหนด g
ใช้เมื่อโจทย์ไม่กำหนด g
3. 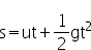 ใช้เมื่อโจทย์ไม่กำหนด v
ใช้เมื่อโจทย์ไม่กำหนด v
4 .![]() ใช้เมื่อโจทย์ไม่กำหนด t
ใช้เมื่อโจทย์ไม่กำหนด t
5.  ใช้เมื่อโจทย์ถาม s ในวินาทีที่ n
ใช้เมื่อโจทย์ถาม s ในวินาทีที่ n
คล้ายกับการเคลื่อนที่ในแนวเส้นตรง เพื่อความไม่สับสนจะทบทวนความหมายของตัวแปรที่เกี่ยวข้องดังนี้
u คือ ความเร็วต้น มีหน่วยเป็น เมตร/วินาที (m/S)
v คือ ความเร็วปลาย มีหน่วยเป็น เมตร/วินาที (m/S)
t คือ เวลา มีหน่วยเป็น วินาที (S)
s คือ การกระจัด มีหน่วยเป็น เมตร (m)
g คือ ความเร่งเนื่องจากความโน้มถ่วงของโลก มีหน่วยเป็น เมตร/วินาที
หมายเหตุ ในที่นี้สมการที่ใช้้ในการคำนวณข้างต้น เป็นการพิจารณาขนาดของปริมาณที่เกี่ยวข้อง และการกำหนดทิศทาง กำหนดดังนี้
1. ทิศ u ต้อง เป็น + เสมอ ปริมาณใด ตรงข้ามกับ u จะมีค่าเป็น –
2. การกระจัดต้องวัดจากจุดเริ่มต้น และพิจารณาประกอบกับ u
4. กราฟการเคลื่อนที่เเนวเส้นตรง (Rectilinear motion Graphical Interpretation)
กราฟการเคลื่อนที่ด้วยความเร็ว คงที่ ควาเร่งเท่ากับศูนย์
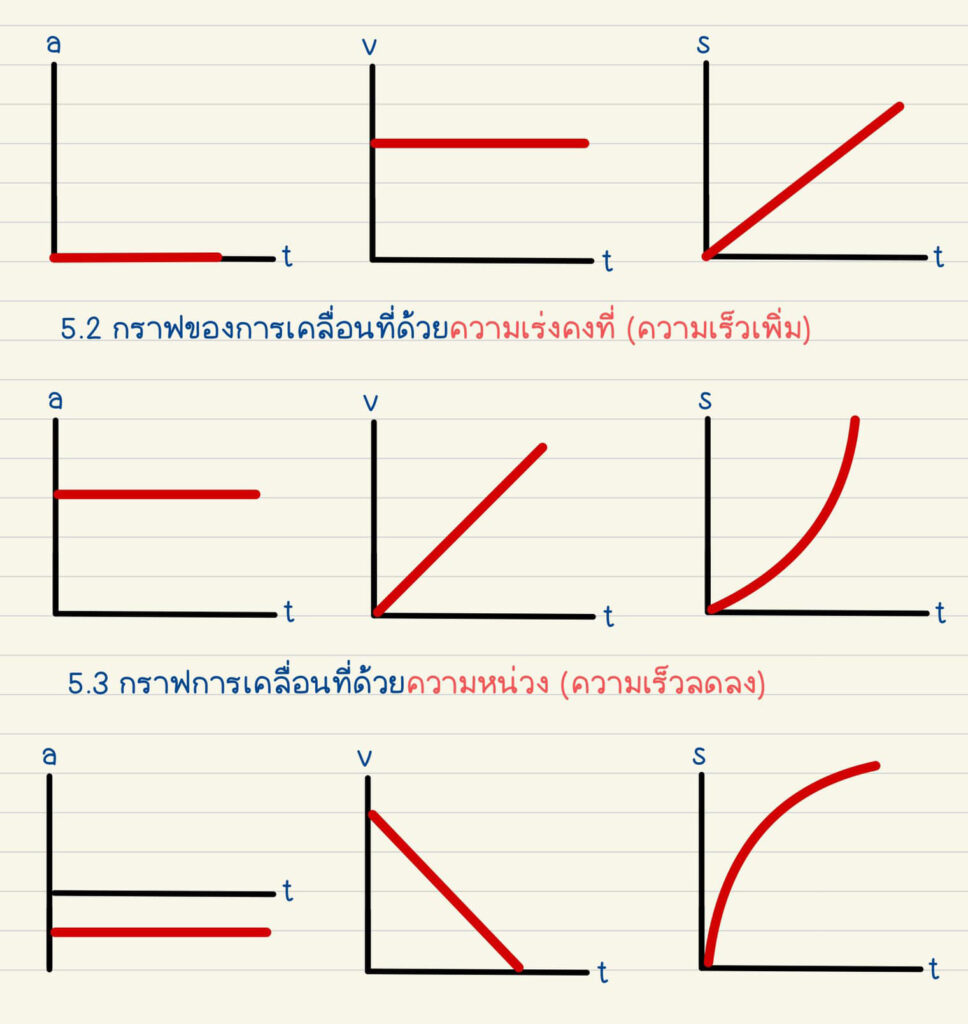
-ขอบคุณรูปกราฟ จาก https://www.facebook.com/kruphysics8
ขอบคุณข้อมูล http://www.scimath.org