การเคลื่อนที่แบบต่าง ๆ (โพรเจกไทล์,วงกลม,ทางโค้ง)ฟิสิกส์ ม.ปลาย

การเคลื่อนที่แบบโปรเจกไทล์

  โพรเจกไทล์(Projectile) หมายถึงวัตถุที่ขว้างหรือยิงออกไปทั้งนี้ในบริเวณใกล้ผิวโลกตามปกติการเคลื่นที่ของวัตถุดังกล่าว  จะสังเกตได้ว่ามีวิถีโค้งการเคลื่อนที่ตามรูปแบบที่วัตถุดังกล่าวเคลื่อนที่ที่ไปโดยเฉพาะเมื่อไม่มีแรงต้านทานของอากาศ  หรือแรงต้านทานมีผลน้อยจนไม่ต้องนำมาคิด จะเรียกว่าการเคลื่นที่แบบโพรเจกไทล์ในกรณีที่แรงต้านทานของอากาศมีผล  ต่อการเคลื่อนไหวที่เนื่องจากวัตถุเบา  หรือเนื่องจากการเคลื่อนที่เร็วและมีการหมุน วิถีการเคลื่อนที่จะแตกต่างออกไปจากการเคลื่อนที่แบบโพรเจกไทล์ และไม่นับเป็นการเคลื่อนที่แบบโพรเจกไทล์ เช่น การเคลื่นที่ของลูกแบดมินตัน ลูกกอล์ฟการเคลื่อนที่แบบโปรเจกไทล์เป็นการเคลื่อนไหวแบบ2มิติคือเคลื่อนที่ในระดับ  และแนวดิ่งพร้อมกันในแนวดิ่งเป็นการเคลื่อนที่  ที่มีความเร่งเนื่องจากแรงโน้มถ่วงของโลกในขณะที่แนวราบไม่มีความเร่งเพราะไม่มีแรงกระทำในแนวระดับ

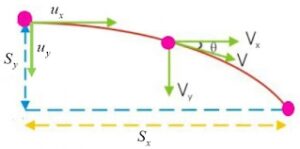
 การเคลื่อนที่แบบโพรเจกไทล์ หมายถึง การเคลื่อนที่ของวัตถุที่ประกอบด้วยการเคลื่อนที่ 2 แนวตั้งฉากกัน และเกิดขึ้นในเวลาเดียวกัน เช่น การขี่จักรยานผาดโผน เป็นเส้นทางโค้งจากเนินด้านหนึ่งไปยังเนินอีกด้านหนึ่ง การเคลื่อนที่ของวัตถุที่ถูกขว้างขึ้นไปในอากาศในแนวที่ทำมุม θ ใด ๆ  กับแนวราบด้วยอัตราเร็ว u เราสามารถวิเคราะห์ความเร็วการเคลื่อนที่ของวัตถุออกมาได้ดังภาพ

ลักษณะการเคลื่อนที่แบบโปรเจกไทล์

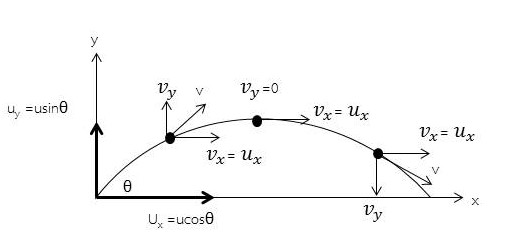
X ความเร็วต้นในแนวราบ = ucos θ

และ

Y ความเร็วต้นในแนวดิ่ง = usin θ

 การเคลื่อนที่แบบโปรเจกไทล์ เป็นการเคลื่อนที่ 2 แนวพร้อมกัน คือ แนวระดับ และแนวดิ่ง ซึ่งพบว่า ความเร็วในแนวระดับ ไม่มีผลต่อการเคลื่อนที่ในแนวดิ่ง โดยจากการทดลองปล่อยวัตถุให้ตกอย่างอิสระ พร้อมกับวัตถุที่ถูกดีดออกไปในแนวระดับ พบว่า เมื่อใช้แรงมากวัตถุที่ถูกดีดจะตกไกล แต่ตกถึงพื้นพร้อมกับวัตถุที่ตกในแนวดิ่ง แสดงว่า การเคลื่อนที่ในแนวระดับไม่มีผลต่อการเคลื่อนที่ในแนวดิ่ง ดังนั้นเราจึงแยกพิจารณาการเคลื่อนที่ออกเป็น 2 แนว คือ ในแนวดิ่ง และในแนวระดับ

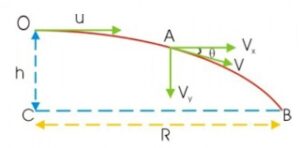
        การเคลื่อนที่ในแนวระดับ
พิจารณาการเคลื่อนที่ของวัตถุในอากาศ ขณะที่วัตถุลอยในอากาศ มีแรงกระทำต่อวัตถุเพียงแรงเดียว คือ แรงดึงดูดของโลก  (ไม่คิดแรงต้านอากาศ) ในทิศเข้าสู่ศูนย์กลางของโลก หรือในแนวดิ่ง ดังนั้น ในแนวระดับจึงไม่มีแรงกระทำต่อวัตถุ หรือแรงลัพธ์ที่กระทำต่อวัตถุในแนวระดับเป็นศูนย์ 

    จากกฎการเคลื่อนที่ของนิวตัน เราพบว่า เมื่อไม่มีแรงลัพธ์มากระทำต่อวัตถุ วัตถุจะรักษาสภาพการเคลื่อนที่ให้คงที่ ผลคือ วัตถุเคลื่อนที่ด้วยความเร็วคงที่ 

    ดังนั้น การเคลื่อนที่ในแนวระดับของการเคลื่อนที่แบบโปรเจกไทล์ สามารถหาการกระจัดในแนวระดับได้ตามสมการ

เมื่อ Sx =  การกระจัดในแนวระดับ  ( m )

    Ux =  ความเร็วในแนวระดับ  (m/s)

   t   =  ช่วงเวลาของการเคลื่อนที (s)

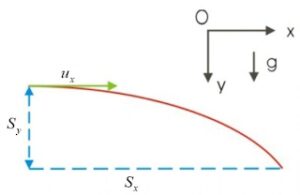
การเคลื่อนที่ในแนวดิ่ง
            เมื่อพิจารณาการเคลื่อนที่ในแนวดิ่ง พบว่า วัตถุมีแรงกระทำในแนวดิ่ง คือ แรงโน้มถ่วงของโลก  G  ดังนั้น วัตถุเคลื่อนที่ในแนวดิ่งด้วยความเร่ง ay ซึ่งมีค่าเท่ากับ G ความเร่งเนื่องจากความโน้มถ่วงของโลก

            ดังนั้น การเคลื่อนที่ของวัตถุแบบโปรเจกไทล์ในแนวดิ่ง เหมือนวัตถุที่ตกอย่างอิสระทุกประการ ซึ่งสมการการเคลื่อนที่ของวัตถุในแนวดิ่ง คือ

            ความเร็ว   

            

การกระจัด

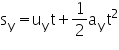
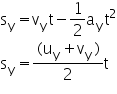
              โดยที่           

        สรุปการเคลื่อนที่แบบโปรเจกไทล์
1. วัตถุเคลื่อนที่อย่างอิสระ มีแรงดึงดูดของโลก  กระทำเพียงแรงเดียว

2. วัตถุต้องมีความเร็วต้นในแนวระดับ ส่วนในแนวดิ่ง จะมีหรือไม่ก็ได้ โดย ความเร็วในแนวระดับคงที่เสมอ

3. เวลาที่ใช้ในการเคลื่อนที่ในแนวระดับ เท่ากับ ในแนวดิ่ง

4. การพิจารณาปริมาณในแนวดิ่ง ปริมาณที่มีทิศตรงข้ามกับความเร็วต้น ให้มีเครื่องหมายติดลบ เช่น การขว้างวัตถุขึ้นในแนวดิ่ง พบว่า   เป็นต้น

5. การคำนวณปริมาณต่างในการเคลื่อนที่ ใช้สมการการเคลื่อนที่เหมือนการเคลื่อนที่ในแนวตรง แต่แยกพิจารณาในแนวดิ่ง (ความเร็วคงที่) และในแนวระดับ (การตกอย่างอิสระ)

การเคลื่อนที่แบบวงกลม

 วัตถุที่เคลื่อนที่เป็นวงกลม บนระนาบใดๆ อัตราเร็วขณะใดขณะหนึ่งของวัตถุจะคงที่หรือไม่ก็ได้ แต่ความเร็วของวัตถุไม่คงที่แน่นอน เนื่องจากว่ามีการเปลี่ยนทิศาทางของการเคลื่อนที่ ตลอดเวลา ซึ่งเมื่อวัตถุที่มีการเปลี่ยนทิศทางการเคลื่อนที่แสดงว่า วัตถุนี้ต้องมีองค์ประกอบของแรงมากระทำในทิศทางที่ตั้งฉากกับเส้นทางการเคลื่อนที่ด้วย และกรณีที่การเคลื่อนที่มีอัตราเร็วไม่คงที่ แสดงว่าต้องมีองค์ประกอบของแรงในทิศทางที่ขนานกับแนวการเคลื่อนที่ด้วย พิจารณา รูป

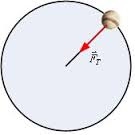
การเคลื่อนที่แบบวงกลมจัดเป็นหนึ่งในการเคลื่อนที่แบบ 2 มิติ ในการเคลื่อนที่เป็นวงกลมที่จะทำการศึกษานั้น ความเร็วของวัตถุที่เคลื่อนที่เป็นวงกลมจะมีค่าคงที่หรือเท่ากันตลอดการเคลื่อนที่เรียกการเคลื่อนที่วงกลมแบบนี้ว่า การเคลื่อนที่เป็นวงกลมสม่ำเสมอ (Uniform Circular Motion)

     การเคลื่อนที่เป็นวงกลม ลักษณะการเคลื่อนที่ของวัตถุจะมี  แรงกระทำตั้งฉากกับเวกเตอร์ความเร็วเสมอตลอดการเคลื่อนที่ วัตถุจะเคลื่อนที่ด้วยความเร็วคงที่ในแนววงกลม แต่ยังคงมีความเร่งเกิดขึ้น ซึ่งความเร่งจะขึ้นกับการเปลี่ยนเวกเตอร์ความเร็ว ซึ่งเวกเตอร์ความเร็วจะมีทิศสัมผัสกับเส้นทางการเคลื่อนที่ของวัตถุและมีทิศตั้งฉากกับแนวรัศมีวงกลม เรียกความเร่งชนิดนี้ว่า ความเร่งแนวสัมผัสวงกลม ( aT)  

    เวกเตอร์ความเร่งในการเคลื่อนที่แบบวงกลมจะมีทิศตั้งฉากกับเส้นทางการเคลื่อนที่ของวัตถุและมีทิศพุ่งเข้าสู่จุดศูนย์กลางวงกลมเสมอ เราเรียกความเร่งนี้ว่า ความเร่งสู่ศูนย์กลาง  (ac )

    คาบ (T)  คือ เวลาที่ใช้ในการเคลื่อนที่ครบ 1 รอบ หรือ วินาทีต่อรอบ (s)
    ความถี่  (f) คือ จำนวนรอบที่เคลื่อนที่ได้ในหนึ่งหน่วยเวลา หรือ รอบต่อวินาที  (Hz)    เมื่อวัตถุเคลื่อนที่แบบวงกลมด้วยอัตราเร็วคงที่ คาบ และความถี่จะมีค่าคงที่ โดยคาบและความถี่สัมพันธ์กันโดย        

อัตราเร็วเชิงเส้น (v)   คือ ระยะทางตามแนวเส้นรอบวงของวงกลมที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา ( m/s)      

 ความเร่งสู่ศูนย์กลาง  วัตถุที่เคลื่อนที่ เป็นวงกลมจะเกิดความเร่ง 2 แนว คือ ความเร็วแนวเส้นสัมผัสวงกลม และความเร่งแนวรัศมีหรือความเร่งสู่ศูนย์กลาง
ถ้าวัตถุเคลื่อนที่ด้วยอัตราเร็วคงที่ เช่น วงกลมในแนวระนาบจะเกิดความเร่งสู่ศูนย์กลางเพียงแนวเดียว
การที่วัตถุมีอัตราเร็วเท่าเดิม แต่ทิศทางเปลี่ยนแปลงตลอดเวลา ย่อมหมายความว่า ต้องมีความเร็วอื่นมาเกี่ยวข้องด้วย ความเร็วที่มาเกี่ยวข้องนี้จะพิสูจน์ได้ว่า มีทิศทางเข้าสู่จุดศูนย์กลางของการเคลื่อนที่ และความเร็วนี้เมื่อเทียบกับเวลาจะเป็นความเร่งซึ่งมีค่า        

การหาแรงที่ทำให้วัตถุเคลื่อนที่แบบวงกลม           

 จากกฎการเคลื่อนที่ ข้อที่สองของนิวตัน และการเคลื่อนที่แบบวงกลม แรงลัพธ์ที่มากระทำต่อวัตถุกับความเร่งของวัตถุจะมีทิศทางเดียวกัน คือทิศพุ่งเข้าหาจุดศูนย์กลาง ซึ่งเขียนเป็นสมการได้ว่า        อัตราเร็วเชิงมุม (Angular speed)                  อัตราเร็วของวัตถุที่ เคลื่อนที่แบบวงกลมที่กล่าวมาแล้วนั้นคือความยาวของเส้นโค้งที่วัตถุเคลื่อน ที่ได้ในเวลา 1 วินาที ซึ่งเราอาจเรียกอีกอย่างหนึ่งว่า อัตราเร็วเชิงเส้น (v)           แต่ในที่นี้ยังมีอัตราเร็วอีกประเภทหนึ่ง ซึ่งเป็นการบอกอัตราการเปลี่ยนแปลงของมุมที่จุดศูนย์กลาง เนื่องจากการกวาดไปของรัศมี ใน 1 วินาที เรียกว่า อัตราเร็วเชิงมุม (w) อ่านว่า โอเมก้า           นิยามอัตราเชิงมุม (w) คือ มุมที่รัศมีกวาดไปได้ใน 1 วินาทีมีหน่วยเป็น เรเดียน/วินาที    การบอกมุมนอกจากจะมีหน่วยเป็นองศาแล้ว ยังอาจใช้หน่วยเป็นเรเดียน (radian) โดยมีนิยามว่า มุม 1 เรเดียน มีค่าเท่ากับมุมที่จุดศุนย์กลางของวงกลม ซึ่งมีเส้นโค้งรองรับมุมยาวเท่ากับรัศมี หรือกล่าวได้ว่ามุมในหน่วยเรเดียน คือ อัตราส่วนระหว่างส่วนเส้นโค้งที่รองรับมุมกับรัศมีของวงกลม           ถ้า a คือ ความยาวองส่วนโค้งที่รองรับมุม           r   คือ รัศมีของส่วนโค้ง          q  คือ มุมที่จุดศูนย์กลางเป็นเรเดียน        ความสัมพันธ์ระหว่างมุมในหน่วยองศากับเรเดียน           เมื่อพิจารณาวงกลม พบว่ามุมรอบจุดศูนย์กลางของวงกลมเท่ากับ 360 องศา โดยส่วนโค้งที่รองรับมุมก็คือเส้นรอบวงนั้นเอง    ดังนั้น สรุปได้ว่า มุม 360 องศา เทียบเท่ากับมุม 2p เรเดียน เมื่อพิจารณาวัตถุเคลื่อนที่แบบวงกลมด้วยอัตราเร็วคงที่ครบ 1 รอบพอดี    ซึ่งเป็นความสัมพันธ์ระหว่างอัตราเร็วเชิงเส้น (v) และอัตราเร็วเชิงมุม (w)