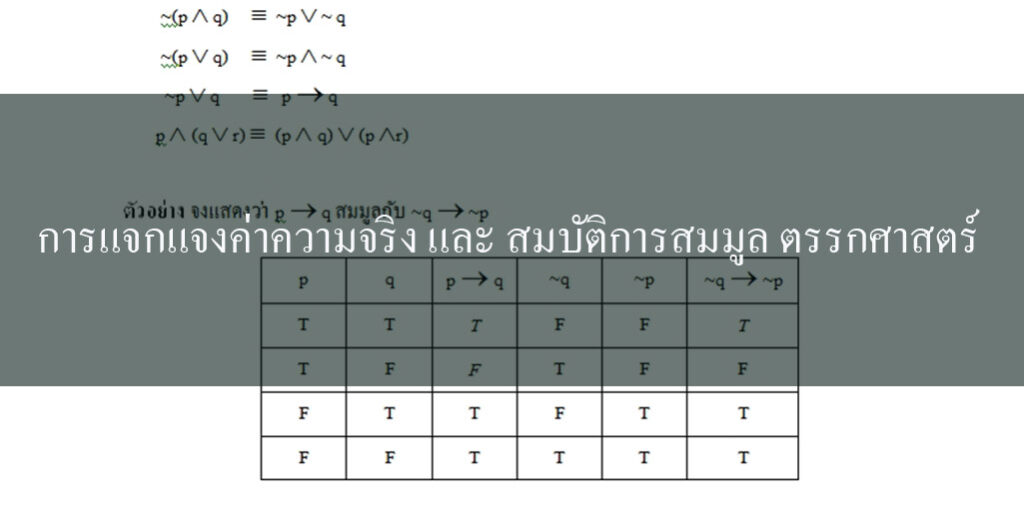
การแจกแจงค่าความจริง ตรรกศาสตร์ โดยมีเนื้อหาตั้งแต่ สมบัติการสมมูล ประพจน์ การหาค่าความจริง สัจนิรันดร์ การอ้างเหตุผล และตัวบ่งปริมาณ
การแจกแจงค่าความจริง
จริง ใช้สัญลักษณ์ T
เท็จ ใช้สัญลักษณ์ F
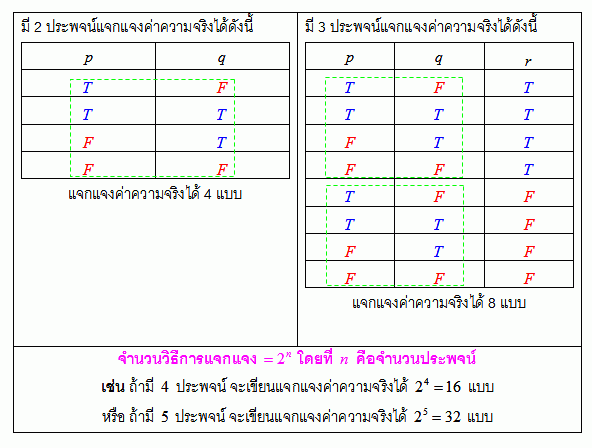
การแจกแจงค่าความจริง ตรรกศาสตร์


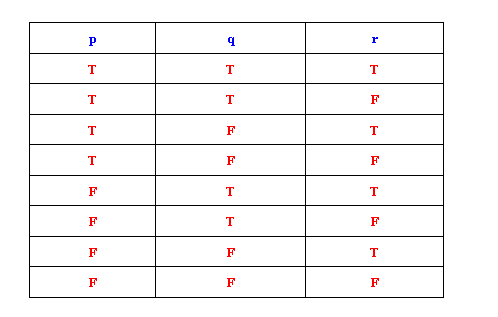
ตัวเชื่อม (connective)
1. ตัวเชื่อม “และ” เป็นตัวเชื่อมระหว่างประพจน์สองประพจน์ ซึ่งใช้สัญลักษณ์ ∧ (อ่านว่า และ) แทนคำว่า “และ” ดังนั้นเมื่อเชื่อมประพจน์ p , q ด้วยตัวเชื่อม “และ” จะได้ประพจน์ ” p และ q ”
เขียนแทนด้วย p ∧ q (อ่านว่า พีและคิว)
2. ตัวเชื่อม “หรือ” เป็นตัวเชื่อมระหว่างประพจน์สองประพจน์ ซึ่งใช้สัญลักษณ์ ∨ (อ่านว่า หรือ) แทนคำว่า “หรือ” ดังนั้นเมื่อเชื่อมประพจน์ p , q ด้วยตัวเชื่อม “หรือ” จะได้ประพจน์ ” p หรือ q ”
เขียนแทนด้วย p ∨ q (อ่านว่า พีหรือคิว)
3. ตัวเชื่อม “ถ้า….แล้ว” เป็นตัวเชื่อมระหว่างประพจน์สองประพจน์ โดยที่ประพจน์หนึ่งอยู่หลังคำว่า “ถ้า” ส่วนอีกประพจน์หนึ่งอยู่หลังคำว่า “แล้ว” ตัวเชื่อม “ถ้ว…แล้ว” เป็นตัวเชื่อมที่สำคัญมากในทางคณิตศาสตร์ เพราะเป็นตัวเชื่อมที่แสดงความเป็น “เหตุ” เป็น “ผล” ซึ่งใช้สัญลักษณ์→ (อ่านว่า ถ้า…แล้ว) แทนคำว่า “ถ้า…แล้ว” ดังนั้นเมื่อเชื่อมประพจน์ p , q ด้วยตัวเชื่อม “ถ้า…แล้ว” จะได้ประพจน์ ” ถ้า p แล้ว q ”
เขียนแทนด้วย p → q (อ่านว่า ถ้า…พี…แล้ว…คิว)
4. ตัวเชื่อม “ก็ต่อเมื่อ” เป็นตัวเชื่อมระหว่างประพจน์สองประพจน์ ที่ใช้สัญลักษณ์ ⇔ หรือ ⇔ (อ่านว่า ก็ต่อเมื่อ) แทนคำว่า “ก็ต่อเมื่อ” ดังนั้นเมื่อ เชื่อมประพจน์ p , q ด้วยตัวเชื่อม “ก็ต่อเมื่อ” จะได้ประพจน์ ” p ก็ต่อเมื่อq ”
เขียนแทนด้วย p ⇔ q (อ่านว่า พี ก็ต่อเมื่อ คิว)
ประพจน์ p → q มีความหมายในเชิง “ถ้า…แล้ว…” ดังนี้
( p → q ) ∧ ( q → p )
ซึ่งหมายความว่า ถ้า p เป็นเหตุแล้วจะได้ผล q และในทางกลับกัน ถ้า q เป็นเหตุแล้วจะได้ผล p
กำหนดให้ p และ q เป็นประพจน์ใดๆ
| เราสามารถเชื่อมประพจน์ทั้งสองเข้าด้วยกันได้ โดยอาศัยตัวเชื่อมประพจน์ดังต่อไปนี้ | ||
|
1.
|
ตัวเชื่อมประพจน์ “และ” | |
| การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “และ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∧ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงเป็นจริง (T) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นเท็จ (F) | ||
|
2.
|
ตัวเชื่อมประพจน์ “หรือ” | |
| การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “หรือ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∨q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงเป็นเท็จ (F) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นจริง (T) | ||
|
3.
|
ตัวเชื่อมประพจน์ “ถ้า…แล้ว” | |
| การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ถ้า…แล้ว” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p → q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p เป็นจริง (T) และ q เป็นเท็จ (F) นอกนั้นมีค่าความจริงเป็นจริง (T) | ||
|
4.
|
ตัวเชื่อมประพจน์ “ก็ต่อเมื่อ” | |
| การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ก็ต่อเมื่อ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ⇔ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงตรงกัน และจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงตรงข้ามกัน | ||
|
5.
|
นิเสธของประพจน์ | |
|
นิเสธของประพจน์ใดๆ คือ ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ และสามารถเขียนแทนนิเสธของ p ได้ด้วย ~p
|
||
ประพจน์การสมมูลกัน ตัวเชื่อม (connective)
ประพจน์ที่เป็นนิเสธกัน
ประพจน์ 2 ประพจน์เป็นนิเสธกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงตรงข้ามกันทุกกรณีของค่าความจริงของประพจน์ย่อย
ตัวอย่างประพจน์ที่เป็นนิเสธกันที่ควรทราบ มีดังนี้
~(p ∧ q) สมมูลกับ ~p ∨ ~q
~(p ∨ q) สมมูลกับ ~p ∧ ~q
~(p → q) สมมูลกับ p ∧ ~q
~(p ⇔ q) สมมูลกับ (p ⇔ ~q) ∨(q ⇔ ~p)
~(p ⇔ q) สมมูลกับ (p ∧ ~q) ∨ ( q ∧~p)
สมบัติการสมมูล
- สมบัติการสลับที่
p ∧ q ≡ q ∧ p
p ∨ q ≡ q ∨ p
p ↔ q ≡ q ↔ p
- สมบัติการเปลี่ยนกลุ่ม
p ∧ ( q ∧ r ) ≡ ( p ∧ q ) ∧ r ≡ p ∧ q ∧ r
p ∨ ( q ∨ r ) ≡ ( p ∨ q ) ∨ r ≡ p ∨ q ∨ r
p ↔ ( q ↔ r ) ≡ ( p ↔ q ) ↔ r ≡ p ↔ q ↔ r
- สมบัติการแจกแจง
p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r )
p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r )
p → ( q ∨ r ) ≡ ( p → q ) ∨ ( p → r )
p → ( q ∧ r ) ≡ ( p → q ) ∧ ( p → r )
( p ∨ q ) → r ≡ ( p → r ) ∧ ( p → r )
( p ∧ q ) → r ≡ ( p → r ) ∨ ( p → r )
- สมบัติของ ถ้า…แล้ว ( → )
p → q ≡ ~q → ~p ≡ ~p ∨ q
- สมบัติของ ก็ต่อเมื่อ ( ↔ )
p ↔ q ≡ ( p → q ) ∧ (q → p )
- สมบัติของ นิเสธ ( ~ )
~(~p) ≡ p
~(p ∧ q) ≡ ~p ∨ ~q
~(p ∨ q) ≡ ~p ∧ ~q
~(p → q) ≡ p ∧ ~q
~(p ↔ q) ≡ ~p ↔ q ≡ p ↔ ~q
- สมบัติอื่น ๆ
p ∧ p ≡ p
p ∧ T ≡ p
p ∧ F ≡ F
p ∧ ~p ≡ F
p ∨ p ≡ p
p ∨ T ≡ T
p ∨ F ≡ p
p ∨ ~p ≡ T
p → F ≡ ~p
F → p ≡ T
p → T ≡ T
T → P ≡ P
P ↔ P ≡ T
P ↔ ∼P ≡ F