การแปลงทางเรขาคณิต – การสะท้อน
การสะท้อน
การสะท้อน ( Reflection ) เป็นการแปลงที่จุดทุกจุดของรูปต้นแบบเคลื่อนที่ข้ามเส้นตรงเส้นหนึ่ง ซึ่งเปรียบเหมือนกระจกหรือเรียกว่าเส้นสะท้อน โดยที่เส้นนี้จะแบ่งครึ่ง
และตั้งฉากกับส่วนของเส้นตรงที่เชื่อมระหว่างจุดแต่ละจุดบนรูปต้นแบบกับจุดแต่ละจุดบนรูปสะท้อนที่สมนัยกัน
สมบัติของการสะท้อน
1. รูปที่เกิดจากการสะท้อนมีขนาดและรูปร่างเท่ากับรูปต้นแบบ หรือเท่ากันทุกประการกับรูปต้นแบบ
2. รูปที่เกิดจากการสะท้อนกับรูปต้นแบบห่างจากเส้นสะท้อนเท่ากัน
3. จุดบนเส้นสะท้อนเป็นจุดคงที่ ไม่มีการสะท้อน
การสะท้อนข้ามแกน X
ความหมายของการสะท้อนข้ามแกน X
ในแง่ภาษา หมายถึง การสะท้อนจุดข้ามแกน X ใช้ค่าพิกัด X เดียวกัน และคูณค่าพิกัด Y ด้วย – 1
ในแง่พีชคณิต หมายถึง ( X, Y ) กลายเป็น ( X, -Y )
การสะท้อนข้ามแกน Y
ความหมายของการสะท้อนข้ามแกน Y
ในแง่ภาษา หมายถึง การสะท้อนจุดข้ามแกน Y คูณค่าพิกัด X ด้วย – 1 และใช้ค่าพิกัด Y เดิม
ในแง่พีชคณิต หมายถึง ( X, Y ) กลายเป็น (- X, Y )

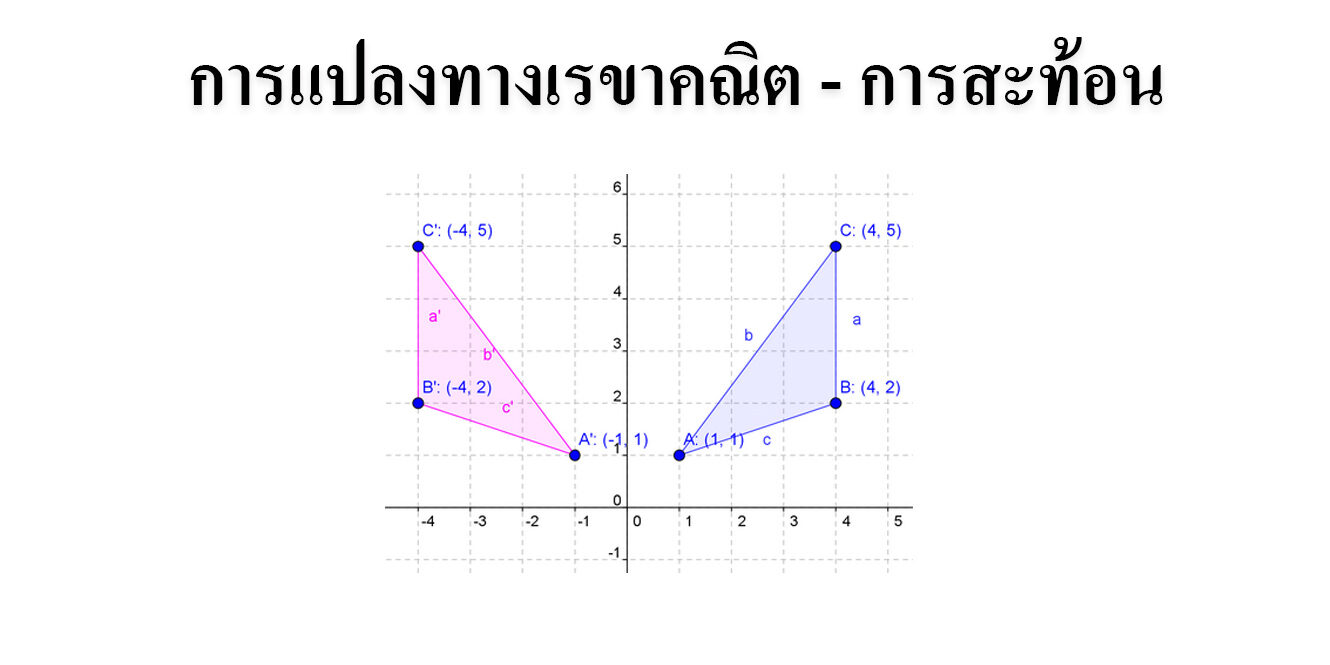
จากภาพแสดงการสะท้อนของ ΔABC เป็นการสะท้อนข้ามแกน Y
การเลื่อนขนาน
การเลื่อนขนานต้องมีรูปต้นแบบ ทิศทางและระยะทางที่ต้องการเลื่อนรูป การเลื่อนขนานเป็นการแปลงที่จับคู่จุดแต่ละจุดของรูปที่ได้จากการเลื่อนรูปต้นแบบไปในทางทิศทางใดทิศทางหนึ่งด้วยระยะทางที่กำหนด จุดแต่ละจุดบนรูปที่ได้จากการเลื่อนขนานระยะห่างจากจุดที่สมนัยกันบนรูปต้นแบบเป็นระยะทางเท่ากัน การเลื่อนในลักษณะนี้เรียกอีกอย่างหนึ่งว่า “สไลด์ (slide)”
ในการบอกทิศทางและระยะทางของการเลื่อนขนาน จะใช้เวกเตอร์เป็นตัวกำหนด ซึ่งการกำหนด
เวกเตอร์ของการเลื่อนขนานอาจให้จุดเริ่มต้นอยู่บนรูปต้นแบบหรืออยู่นอกรูปต้นแบบก็ได้

โดยสมบัติของการเลื่อนขนานมีดังนี้
1. รูปที่ได้จากการเลื่อนขนานกับรูปต้นแบบเท่ากันทุกประการ
2. จุดแต่ละจุดที่สมนัยกันบนรูปที่ได้จากการเลื่อนขนานกับรูปต้นแบบจะมีระยะห่างเท่ากัน
3. ภายใต้การเลื่อนขนาน จะไม่มีการเปลี่ยนแปลงรูปร่างและขนาดของรูปต้นแบบ
การหมุน
การหมุน ( Rotation )เป็นการแปลงที่จุดทุกจุดของรูปต้นแบบเคลื่อนที่ไปเป็นมุมเดียวกันรอบจุดตรึงอยู่กับที่ที่กำ หนดหรือจุดหมุน การหมุนจะหมุนทวนเข็มนาฬิกาหรือตามเข็มนาฬิกา ตามขนาดของมุมและทิศทางที่ต้องการหมุนโดยทั่วไปถ้าไม่ระบุทิศทางการหมุนจะถือว่าเป็นการหมุนทวนเข็มนาฬิกาการหมุนเป็นการแปลงที่เกิดจากการจับคู่ของ จุดแต่ละคู่ระหว่างรูปต้นแบบกับรูปที่ได้จากการหมุน

สมบัติของการหมุน
1. รูปที่ได้จากการหมุนกับรูปต้นแบบเท่ากันทุกประการ
2. จุดแต่ละจุดบนรูปต้นแบบเคลื่อนที่รอบจุดหมุนด้วยขนาดของมุมที่กำ หนด
3. จุดหมุนเป็นจุดคงที่
ความหมายของการหมุน 90° ทวนเข็มนาฬิกา
ในแง่ภาษา หมายถึง การหมุนรูปทวนเข็มนาฬิกาไป 90° สลับค่าพิกัดแต่ละจุด แล้วคูณค่าพิกัดแรกด้วย -1
ในแง่เลขคณิต หมายถึง A ( 3, 2 ) => A′ (-2 , 3 )
ในแง่พีชคณิต หมายถึง A ( x, y ) => A′ ( – y , x )
ความหมายของการหมุน 180°
ในแง่ภาษา หมายถึง การหมุนไป 180° คูณค่าพิกัดทั้งสองของแต่ละจุดด้วย –1
ในแง่เลขคณิต หมายถึง A ( 3 , 2 ) => A′ (-3 , – 2 )
ในแง่พีชคณิต หมายถึง A ( x, y ) => A′ ( – x , – y )