การแยกตัวประกอบของพหุนาม-คณิตศาสตร์ออนไลน์

การแยกตัวประกอบ คือ การเขียนพหุนามในรูปการคูณของพหุนาม ซึ่งตัวประกอบแต่ละวงเล็บต้องมีดีกรีน้อยกว่าพหุนามเดิม โดยที่แต่ละวงเล็บที่ได้ไม่สามารถเขียนได้ไม่สามารถเขียนเป็นรูปการคูณต่อไปได้อีกมีวิธีการแยกตัวประกอบ 8 วิธีคือ

1. ดึงตัวร่วมโดยใช้สมบัติการแจกแจง

จงแยกตัวประกอบของพหุนามต่อไปนี้

1. 7x + 14x²         2. 7x²y³ + 14x⁴ y²   3. 7(x+y)² + 14(x+y)⁵

วิธีที่ 1    7x + 14x²  = 7x(1+2x)

 วิธีที่ 2     7x + 14x²  = (7x)(1) + (7x)(2x)

      = 7x(1+2x)

(2)   7x²y³ + 14x⁴ y²  = 7x² y² (y+2x)²

(3)   7(x+y)² + 14(x+y)⁵ = 7(x+y)² (1+2(x+y)³)

2. สามพจน์แยกเป็น 2 วงเล็บ

จงแยกตัวประกอบของพหุนามต่อไปนี้

1. x² + 8x + 15      2. x² -8x +15

    3. x² + 2x – 15       4. x² – 2x – 15

วิธีทำ  
(1)  x² + 8x + 15  = (x+3)(x+5)

(2) x² -8x +15 = (x-3)(x-5)

(3) x² + 2x – 15 = (x-3)(x+5)

(4) x² – 2x – 15 = (x – 5)(x+3)

ข้อสังเกต

จากข้อ 1 
x² + 8x + 15  = (x+   ) (x+   ) ( ดูจาก 15 และ 8 x)

คิดต่อไปว่าจำนวนนับอะไรคูณกันได้  15  และ และรวมกันได้  8   จะได้ 3  และ 5

ดังนั้น    x² + 8x + 15 เท่ากับ  (x+3)(x+5)

จากข้อ 2

x² -8x +15          =     (x-     )(x-      )

( ดูจาก 15 และ – 8x ต่อไปว่าจำนวนนับอะไรคูณกันได้ 15 และรวมกันได้ 8 จะได้ 3 และ 5)

ดังนั้น    x² -8x +15 = (x-3)(x-5)

จากข้อ 3

x² + 2x – 15 = (x-     )(x+     )  ( ดูจาก – 15)  คิดต่อไปว่าจำนวนนับอะไรคูณกันได้ -15 และต่างกัน 2 จะได้ 3 และ 5 เนื่องจากผลกลางคือ 2x จึงใส่ 5 ไว้ที่บวกและใส่ 3 ไว้ที่ลบ

ดังนั้น    x² + 2x – 15 = (x-3)(x+5)

จากข้อ 4

x² – 2x – 15      =      (x –     )(x+     )  ( ดูจาก – 15)
คิดต่อไปว่าจำนวนนับอะไรคูณกันได้ 15 และ 3 ชั้น 2 จะได้ 3 และ 5 เนื่องจากผลกลางคือ – 2x จึงใส่ 5 ไว้ที่ลบและใส่ 3 ไว้ที่บวก

ดังนั้น   x² – 2x – 15 = (x – 5)(x+3)

3. ผลต่างกำลังสอง ผลต่างกำลังสาม และผลบวกกำลังสาม

1. ผลต่างกำลังสอง

(น-ล)(น+ล) = น² – ล²

2. ผลต่างกำลังสาม

(น-ล)( น²  + 2นล + ล²) = น³ – ล³

3. ผลบวกกำลังสาม

(น+ล)( น²  –  2นล + ล²) =   น³ + ล³

4. การแยกตัวประกอบโดยอาศัยกำลังสองสมบูรณ์

รูปกำลังสองสมบูรณ์มี 2 รูป

1.x² + 2ax + a²      =   (x+a) ²

2.x² – 2ax + a²       =   (x – a)²

5. เพิ่มลดพจน์กลางแล้วแยกผลต่างกำลังสอง

มักพบกับพหุนามดีกรี 4 และมี 3 พจน์

จงแยกตัวประกอบ

1. x⁴ + x²y² + y⁴   = (x² + y²)² – x² y ²

= (x² + y²)² – (xy)²

= (x² + y² – xy)(x² + y² + xy)

6.  4 พจน์จับคู่ให้เกิดวงเล็บร่วม 

หากน้อง ๆ เจอพหุนามดีกรีที่มากกว่าสอง สามารถใช้วิธีนี้ในการแยกตัวประกอบได้ เช่น
การแยกตัวประกอบของพหุนามดีกรีสาม

จงแยกตัวประกอบ

 x ³ + 2 x² -9x  – 18   = (x³ + 2x²)-(9x+18)

= x² (x+2)-9(x+2)

= (x+2)(x² – 9)

= (x+2)(x-3)(x+3)

7. สี่พจน์จัดรูปผลต่างกำลังสอง

จงแยกตัวประกอบ

 x ² + 2 x y + Y² – 36   = (x² + 2xy + y²) -36

= (x+y)² – 6²

= (x+y-6)(x+y+6)

8. ทฤษฎีบทตัวประกอบ 

ทฤษฎีบทเศษเหลือ  x – c หาร p(x) เศษคือ p(c)

ตัวอย่าง
ให้ P(x) = x² – x -2

P(3) = 3² – 3 -2  = 4

สูตรการแยกตัวประกอบพหุนาม

1.(น+ล)² = น²  + 2นล + ล²
2.(น-ล)² = น²  – 2นล + ล²
3.(น-ล)(น+ล) = น² – ล²
4.(น-ล)( น²  + 2นล + ล²) = น³ – ล³
5.(น+ล)( น²  –  2นล + ล²) =   น³ + ล³
6.(น+ล)³  = น³ + 3น² ล + 3นล² + ล³
7.(น-ล)³  = น³ – 3น² ล + 3นล² – ล³

พหุนามดีกรีสองตัวแปรเดียว คือ พหุนามที่เขียนได้ในรูป ax² + bx + c เมื่อ a, b, c เป็นค่าคงตัว ที่ a ≠ 0 และ x เป็นตัวแปร เพื่อความสะดวกในการหาข้อสรุปของวิธีแยกตัวประกอบของหพุนาม  ax² + bx + c  จะเรียก ax² ว่า พจน์หน้า  เรียก bx ว่า พจน์กลาง และเรียก c ว่า พจน์หลัง  ซึ่งการแยกสามารถทำได้ดังนี้

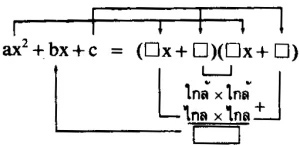
ตัวอย่างเช่น จงแยกตัวประกอบของ  5x² – 11x + 2
ขั้นที่ 1 …แยกพจน์หน้าเป็นสองพจน์ ได้  5x  กับ  x
(5x ……..)(x……..)
ขั้นที่ 2 …แยกพจน์ท้ายออกเป็นสองจำนวนคูณกัน ได้  (-2)×(-1)  นำไปใส่ในขั้นตอนที่ 1 สามารถใส่ได้ 2 แบบ คือ
(5x – 2)(x – 1)  กับ  (5x – 1)(x – 2)
ขั้นที่ 3 …หาพจน์กลางจากขั้นตอนที่ 2 โดยนำ (ใกล้ ×ใกล้) + (ไกล ×ไกล)  ถ้าได้ผลลัพธ์เป็น -11x  แสดงว่าการแยกตัวประกอบนั้นถูกต้อง
ดังนั้น  5x² – 11x + 2  =  (5x – 1)(x – 2)         ตอบ

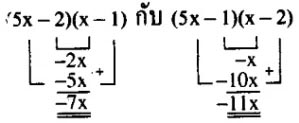
เสริมอีกเพื่อฝึกความแม่นยำ…จงแยกตัวประกอบของพหุนามต่อไปนี้

• 2x² + 9x – 5   =   (2x – 1)(x + 5)
• 15x² – 41x + 28   =   (5x – 7)(3x – 4)
• 18x² + 27x + 10   =   (6x + 5)(3x + 2)
• 5x² – 8x – 21   =   (5x + 7)(x – 3)
• 10x² – 31x + 15   =   (2x – 5)(5x – 3)
• – 5x² + 22x – 8   =   – (5x² – 22x + 8)   =   – (5x – 2)(x – 4)

ขอบคุณข้อมูล https://www.athometh.com/