กำหนดการเชิงเส้น(Linear Programming) หมายถึง ในการทำการ ประกอบกิจการธุรกิจและอุตสาหกรรมตลอดจนทางด้านวิทยาศาสตร์ มี ความจำเป็นที่จะต้องตัดสินใจเพื่อที่จะทำได้ปริมาณบางอย่างมีค่ามาก ที่สุดหรือมีค่าน้อยที่สุด เช่นนำมาใช้ในการจัดสรรทรัพยากร หรือปัจจัยที่ มีอย่างจำกัดเพื่อให้เกิดประโยชน์สูงสุดหรือสูญเสียน้อยที่สุดในการดำเนิน งาน
แบบจำลองกำหนดการเชิงเส้นประกอบด้วย 2 ส่วนดังนี้
- ส่วนที่เราต้องนำไปหาค่าที่เกิดประโยชน์ หรือประสิทธิภาพสูงสุด ส่วนนี้จะอยู่ในรูปสมการ จึงเรียกส่วนนี้ว่า “สมการจุดประสงค์” หรือ “ ฟังก์ชันจุดประสงค์ ”
- ส่
วนที่เป็นทรัพยากรที่มีอยู่อย่างจำกัด ส่วนนี้อยู่ในรูปอสมการที่แสดงถึงเงื่อนไขบังคับ หรือข้อจำกัด “ จึงเรียกส่วนนี้ว่า ” อสมการข้อจำกัด หรือ “เงื่อนไขบังคับ”
หลักการ
- กำหนดให้ P(เป็นข้อความอื่นก็ได้ตามแต่เห็นสมควร) แทนปริมาณที่โจทย์ถา
- มหาค่าต่ำสุด หรือสูงสุด และ x , y แทนปริมาณที่ P ขึ้นอยู่กับมัน
- อ่านข้อมูลจากโจทย์แล้วสรุปเป็นข้อมูลง่ายๆ
- สร้างสมการจุดประสงค์ เนื่องจากสมการจุดประสงค์ เป็นส่วนที่เราต้องนำไปหาค่าที่เกิดประโยชน์
หรือประสิทธิภาพสูงสุด จะได้ สมการจุดประสงค์ P = ax + by เมื่อ a , b E R - สร้างอสมการข้อจำกัด เนื่องจากอสมการข้อจำกัดเป็นส่วนที่เป็นทรัพยากรที่มีอยู่อย่างจำกัด
ส่วนนี้อยู่ในรูปอสมการที่แสดงถึงเงื่อนไขบังคับ หรือข้อจำกัด จะได้ อสมการข้อจำกัดในเทอมของ x
และเทอมของ y
ตัวอย่างที่ 1 บริษัทแห่งหนึ่งผลิตอ่างล้างหน้า 2 ชนิด คือ ชนิด Aและ ชนิดB โดยที่อ่างล้างหน้าชนิดA แต่ละอ่างจะต้องเสียเวลาในการผลิตโดยใช้เครื่องจักร 2 ชั่วโมง ใช้แรงงานคน 1 ชั่วโมง และขายได้กำไรอย่างละ 30 บาท สำหรับอ่างล้างหน้าชนิด B แต่ละอ่างจะต้องเสียเวลาผลิตโยการใช้เครื่องจักร 1 ชั่วโมง ใช้แรงงานคน 3 ชั่วโมง และขายได้กำไร 40 บาท ถ้าวันหนึ่งการผลิตโดยใช้เครื่องจักร และใช้แรงงานคนทำงานไม่เกิน 6 ชั่วโมงและ 8 ชั่วโมง ตามลำดับต้องการทราบว่าบริษัทแห่งนี้ควรผลิตอ่างล้างหน้า
แต่ละชนิดเป็นจำนวนเท่าไรในแต่ละวัน จึงจะได้กำไรมากที่สุด จงสร้างแบบจำลองกำหนดการเชิงเส้น
วิธีทำ 1. กำหนดให้ P แทนปริมาณที่โจทย์ถามหาค่าต่ำสุด หรือสูงสุด
P แทนกำไรทั้งหมด
และ x , y แทนปริมาณที่ P ขึ้นอยู่กับมัน
x แทนจำนวนอ่างล้างหน้าชนิด A ที่ผลิตใน 1 วัน
y แทนจำนวนอ่างล้างหน้าชนิด B ที่ผลิตใน 1 วัน
- อ่านข้อมูลจากโจทย์แล้วสรุปเป็นข้อมูลง่ายๆ ได้ดังนี้
| ชนิดของอ่างล้างหน้า | ใช้เครื่องจักร
(อ่าง/ชม.) |
ใช้แรงงานคน
(อ่าง/ชม.) |
กำไร
(บาท/อ่าง) |
จำนวนที่ผลิตในแต่ละวัน |
| A | 2 | 1 | 30 | x ≥ 0 |
| B | 1 | 3 | 40 | y ≥ 0 |
3.สร้างสมการจุดประสงค์ เนื่องจากสมการจุดประสงค์เป็นส่วนที่เราต้องนำไปหาค่าที่เกิดประโยชน์ หรือประสิทธิภาพสูงสุด
จะได้ สมการจุดประสงค์ P = 30x + 40y
- สร้างอสมการข้อจำกัด เนื่องจากอสมการข้อจำกัดเป็นส่วนที่เป็นทรัพยากรที่มีอยู่อย่างจำกัดส่วนนี้อยู่ในรูปอสมการที่แสดงถึงเงื่อนไขบังคับหรือข้อจำกัด
4.1 เวลาที่ใช้เครื่องจักรผลิตอ่างล้างหน้าชนิด A 2x
เวลาที่ใช้เครื่องจักรผลิตอ่างล้างหน้าชนิด B 1y
เนื่องจากโจทย์บอกว่าใช้เครื่องจักรทำงานในแต่ละวันไม่เกิน 6 ชั่วโมง
จะได้ 2x + y ≤ 6
4.2 เวลาที่ใช้แรงงานคนผลิตอ่างล้างหน้า ชนิด A 1x ชั่วโมง
เวลาที่ใช้แรงงานคนผลิตอ่างล้างหน้า ชนิด B 3y ชั่วโมง
จะได้ x + 3y ≤ 8
4.3 จำนวนอ่างล้างหน้าจะต้องไม่เป็นลบ
จะได้ x ≥ 0, y ≥ 0
แบบจำลองกำหนดการเชิงเส้นประกอบไปด้วย
- สมการจุดประสงค์ คือ กำไรที่ต้องการมากที่สุด มีสมการ คือ P = 30x + 40y
- อสมการข้อจำกัด คือ
2x+ y ≤ 6
x+3y ≤ 8
x ≥ 0
y ≥ 0
ดังนั้น สามารถเขียนตารางสรุปเพื่อให้ชัดเจนได้ดังนี้
| ชนิดของอ่างล้างหน้า | ใช้เครื่องจักร
(อ่าง/ชม.) |
ใช้แรงงานคน
(อ่าง/ชม.) |
กำไร
(บาท/อ่าง) |
จำนวนที่ผลิตในแต่ละวัน |
| A | 2 | 1 | 30 | x ≥ 0 |
| B | 1 | 3 | 40 | y ≥ 0 |
| ข้อจำกัด | 2x + y ≤ 6 | x + 3y ≤ 8 | P = 30x + 40y |
การแก้ปัญหากำหนดการเชิงเส้นโดยวิธีการใช้กราฟ
ในการแก้ปัญหากำหนดการเชิงเส้นนั้นต้องเริ่มต้นด้วยการสร้างแบบจำลองทางคณิตศาสตร์ ซึ่งประกอบด้วย 2 ส่วน คือ
ส่วนที่ 1 ส่วนที่เป็นเป้าหมาย จะอยู่ในรูปของ สมการจุดประสงค์ (ในเอกสารเล่มนี้ใช้ P)
ส่วนที่ 2 ส่วนที่เป็นข้อจำกัด จะอยู่ในรูปของ อสมการข้อจำกัด
ซึ่งเป็นการแปลงสถานการณ์ปัญหาให้เป็นปัญหาทางคณิตศาสตร์ จากนั้นจึงหาคำตอบของปัญหาด้วยวิธีการต่าง ๆ ในการศึกษาครั้งนี้ใช้การกราฟช่วยในการหาคำตอบ
ข้อกำหนด
- ถ้ากำหนดการเชิงเส้น มีคำตอบที่เหมาะสมเพียงคำตอบเดียว แล้วคำตอบนั้นจะต้องอยู่ที่จุดหักมุมกราฟ
ของระบบอสมการข้อจำกัด - ถ้าสมการจุดประสงค์มีค่าน้อยที่สุด หรือมากที่สุด ณ. จุดหักมุม 2 จุดที่มีแขนของจุดหักมุมร่วมกัน
แล้วสมการจุดประสงค์ดังกล่าวจะมีค่าน้อยที่สุด หรือมากที่สุด ณ. จุดทุกจุดบนส่วนของเส้นตรง
ที่เชื่อมจุดหักมุม 2 จุดนั้น แสดงว่าคำตอบที่เหมาะสม จะมีจำนวนนับไม่ถ้วน
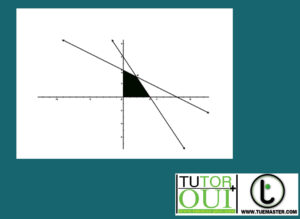
ลองสมมติให้กราฟของระบบอสมการข้อจำกัด เป็นดังนี้
นำความจริงจากข้อกำหนดมาวิเคราะห์ กราฟของระบบสมการข้อจำกัดดังนี้
- จุดทุกจุดในบริเวณส่วนที่แรเงาจะสอดคล้องกับระบบอสมการข้อจำกัด ถูกเรียกว่า
“เซตของคำตอบที่เป็นไปได้” - 2. จากเซตของคำตอบที่เป็นไปได้ เราจะนำไปหาจุดใดที่สดคล้องกับสมการจุดประสงค์ที่ให้ค่าน้อยที่สุด
หรือค่ามากที่สุดจากกราฟของระบบอสมการข้อจำกัด - จุดทุกจุดในบริเวณส่วนที่แรเงา มีโอกาสเป็นไปได้ที่จะทำให้สมการจุดประสงค์มีค่าน้อยที่สุด
หรือมากที่สุด แต่จุดหักมุมมีโอกาสเป็นไปได้มากกว่า - จุดในบริเวณส่วนที่แรเงาที่ทำให้สมการจุดประสงค์มีค่าน้อยที่สุดหรือมากทีสุดถูกเรียกว่า
คำตอบที่เหมาะสม - ถ้ากำหนดการเชิงเส้นมีคำตอบเดียว แล้วจุด A,B,C และ O จุดใดจุดหนึ่ง จะทำให้สมการจุดประสงค์
มีค่าน้อยที่สุด หรือมากที่สุด - ถ้าจุด A และ B ทำให้สมการจุดประสงมีค่าน้อยที่สุด แล้ว จุดทุกจุดที่อยู่บนส่วนของเส้นตรง AB จะทำ
ให้สมการจุดประสงค์ มีค่าน้อยที่สุดหรือมากที่สุดด้วย แสดงว่าคำตอบที่เหมาะสมจะมีจำนวนนับไม่ถ้วน
เทคนิคการแก้ปัญหากำหนดการเชิงเส้นโดยวิธีใช้กราฟ
หลักการ
- ถ้าโจทย์ที่ให้มาเป็นเรื่องราวที่ให้มาเป็นเรื่องราวที่ไม่ได้บอกตัวแปรออกมาตรงๆ เราซึ่งเป็นผู้อ่านโจทย์
จะต้องตั้งตัวแปรให้เป็นปริมาณต่างๆ จากโจทย์และสร้างสมการจุดประสงค์ กับอสมการข้อจำกัด - เขียนกราฟของระบบอสมการข้อจำกัด เพื่อแสดงจุดทุกจุดในบริเวณส่วนที่แรเงาที่สอดคล้องกับระบบ
อสมการข้อจำกัด - หาจุดหักมุมในบริเวณส่วนที่แรเงา
- นำจุดหักมุมแต่ละจุดไปแทนค่าในสมการจุดประสงค์
4.1 ถ้าได้ค่าน้อยที่สุด (มากที่สุด) เพียงคำตอบเดียว แล้วค่านั้นคือ ค่าน้อยที่สุด (มากที่สุด)
ของสมการจุดประสงค์
4.2 ถ้ามีจุดหักมุม 2 จุด ที่มีแขนของจุดหักมุมร่วมกันทำให้สมการจุดประสงค์ มีค่าน้อยที่สุด
(มากที่สุด)
แล้ว จุดทุกจุดบนแกนของมุมนั้น คือ ค่าน้อยที่สุด(มากที่สุด) ของสมการจุดประสงค์ แสดงว่าคำตอบที่เหมาะสม จะมีจำนวนนับไม่ถ้วน
ตัวอย่างที่ 2 กำหนดให้สมการจุดประสงค์ คือ P = 30x + 50y
และอสมการข้อจำกัด คือ 2x + y ≤ 10
x + 2y ≤ 11
x ≥ 0
y ≥ 0
แล้วจงหาว่า P มีค่ามากที่สุดเป็นเท่าไร
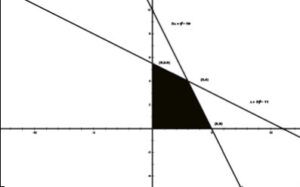
วิธีทำ เขียนกราฟของระบบอสมการข้อจำกัด พร้อมจุดหักมุม
จากรูปจะเห็นได้ว่าจุดหักมุมของรูปสี่เหลี่ยมคือ (0,0) , (0,5.5) , (3,4) และ (5,0) นำจุดหักมุมแทนค่าในจุดประสงค์ ดังตารางต่อไปนี้
| จุดหักมุม (x , y) | P = 30x + 50y |
| (0,0)
(0,5.5) (3,4) (5,0) |
P = 30(0) + 50(0) = 0
P = 30(0) + 50(5.5) = 275 P = 30(3) + 50(4) = 290 P = 30(5) + 50(0) = 150 |
ดังนั้น จากตาราง จะพบว่า ค่ามากที่สุดของ P คือ 290 เมื่อ x = 3 และ y = 4
ตัวอย่างที่ 3 กำหนดให้สมการจุดประสงค์ คือ P = 4x + 3y
และอสมการข้อจำกัด คือ 2x + 3y ≥ 12
2x + y ≥ 8
x ≥ 0
y ≥ 0
แล้วจงหาว่า P มีค่าน้อยที่สุด เป็นเท่าไร
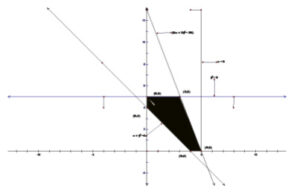
วิธีทำ เขียนกราฟของระบบอสมการข้อจำกัด พร้อมจุดหักมุม
จากรูปจะเห็นได้ว่าจุดหักมุมของรูปเหลี่ยมคือ (6, 0) (3,2) และ(0,8)นำจุดหักมุมแทนค่าในสมการจุดประสงค์ ดังตารางต่อไปนี้
| จุดหักมุม (x , y ) | P = 4x + 3y |
| (6,0)
(3,2) (0,8) |
P = 4(6) + 3(0) = 24
P = 4(3) + 3(2) = 18 P = 4(0) + 3(8) = 24 |
ดังนั้น จากตารางจะพบว่า ค่าน้อยที่สุดของ P คือ18 เมื่อ x = 3 และ y = 2
ตัวอย่างที่ 4 กำหนดให้สมการจุดประสงค์ คือP = 2x + 3y
และอสมการข้อจำกัด คือ x + y ≥ 4 , 5x + 2y ≤ 25
x ≤ 5 , y ≤ 5
x ≥ 0 , y ≥ 0
แล้วจงหาว่า P มีค่ามากที่สุดเป็นเท่าไร
วิธีทำ เขียนกราฟของระบบอสมการข้อจำกัด พร้อมจุดหักมุม
จากรูปจะเห็นได้ว่า จุดหักมุมของรูปเหลี่ยม คือ (0,4) , (0,5) , (3,5) , (5,0) และ (0,4) นำจุดหักมุมแทนค่าในสมการจุดประสงค์ ดังตารางต่อไปนี้
| จุดหักมุม (x , y ) | P = 2x + 3y |
| (0,4)
(0,5) (3,5) (5,0) (4,0) |
P = 2(0) + 3(4) = 12
P = 2(0) + 3(5) = 15 P = 2(3) + 3(5) = 21 P = 2(5) + 3(0) = 10 P = 2(4) + 3(0) = 8 |
ดังนั้น จากตารางจะพบว่าค่ามากที่สุดของ P คือ 21 เมื่อ x = 3 และ y = 5
ตัวอย่างที่ 5 กำหนดให้สมการจุดประสงค์ คือ P = x + 4y
และอสมการข้อจำกัด คือ x + 2y ≥ 8
5x + 2y ≥ 20
x + 4y ≤ 22
x ≥ 0 , y ≥ 0
แล้วจงหาว่า P มีค่าน้อยที่สุดและค่ามากที่สุดเป็นเท่าไร
วิธีทำ เขียนกราฟของระบบอสมการข้อจำกัด พร้อมจุดหักมุม
จากรูปจะเห็นได้ว่าจุดหักมุมของรูปสี่เหลี่ยม คือ (3,2.5) , (2,5) , (22,0) และ (8,0)
นำจุดหักมุมแทนค่าในสมการจุดประสงค์ ดังตารางต่อไปนี้
| จุดหักมุม (x , y ) | P = x + 4y |
| (3,2.5)
(2,5) |
P = 3+ 4(2.5) = 13
P = 2+ 4(5) = 22 P = 22+ 4(0) =22 P = 8+ 4(0) = 8 |
จากตารางจะพบว่า
- ค่าที่น้อยที่สุดของ P คือ 8 เมื่อ x = 8 และ y = 0
- ค่ามากที่สุดของ P คือ 22 ณ. จุดหักมุม (2,5) และ (22,0) ซึ่งเป็นจุดหักมุมที่มีแขนของจุดมุมร่วมกัน
ดังนั้น จุดทุกจุดบนส่วนของเส้นตรงที่เชื่อมจุดหักมุม (2,5)และ(22,0)จะทำให้ค่ามากที่สุดของ P คือ 22
อ้างอิง : https://www.opendurian.com/exercises/pat1_mar_55/19/