กำหนดการเชิงเส้น(Linear Programming) คณิตศาสตร์ ม.6

กำหนดการเชิงเส้น(Linear Programming) หมายถึงในการทำการประกอบกิจการธุรกิจและอุตสาหกรรมตลอดจนทางด้านวิทยาศาสตร์มีความจำเป็นที่จะต้องตัดสินใจเพื่อที่จะทำได้ปริมาณบางอย่างมีค่ามากที่สุดหรือมีค่าน้อยที่สุด เช่นนำมาใช้ในการจัดสรรทรัพยากร หรือปัจจัยที่  มีอย่างจำกัดเพื่อให้เกิดประโยชน์สูงสุดหรือสูญเสียน้อยที่สุดในการดำเนินงาน

 

แบบจำลองกำหนดการเชิงเส้นประกอบด้วย 2 ส่วนดังนี้

1. ส่วนที่เราต้องนำไปหาค่าที่เกิดประโยชน์ หรือประสิทธิภาพสูงสุด ส่วนนี้จะอยู่ในรูปสมการ จึงเรียกส่วนนี้ว่า “สมการจุดประสงค์” หรือ “  ฟังก์ชันจุดประสงค์ ”
2. ส่วนที่เป็นทรัพยากรที่มีอยู่อย่างจำกัด ส่วนนี้อยู่ในรูปอสมการที่แสดงถึงเงื่อนไขบังคับ หรือข้อจำกัด “ จึงเรียกส่วนนี้ว่า ” อสมการข้อจำกัด หรือ “เงื่อนไขบังคับ”

หลักการ

1. กำหนดให้ P(เป็นข้อความอื่นก็ได้ตามแต่เห็นสมควร) แทนปริมาณที่โจทย์ถา
2. มหาค่าต่ำสุดหรือสูงสุด และ x , y แทนปริมาณที่ P ขึ้นอยู่กับมัน

2. อ่านข้อมูลจากโจทย์แล้วสรุปเป็นข้อมูลง่ายๆ
3. สร้างสมการจุดประสงค์ เนื่องจากสมการจุดประสงค์ เป็นส่วนที่เราต้องนำไปหาค่าที่เกิดประโยชน์
   หรือประสิทธิภาพสูงสุด จะได้ สมการจุดประสงค์ P = ax + by เมื่อ a , b E R
4. สร้างอสมการข้อจำกัด เนื่องจากอสมการข้อจำกัดเป็นส่วนที่เป็นทรัพยากรที่มีอยู่อย่างจำกัด
   ส่วนนี้อยู่ในรูปอสมการที่แสดงถึงเงื่อนไขบังคับ หรือข้อจำกัด จะได้ อสมการข้อจำกัดในเทอมของ x
   และเทอมของ y

ตัวอย่าง      บริษัทผลิตโทรทัศน์แห่งหนึ่งผลิตโทรทัศน์ขนาด  14  นิ้ว  อยู่  2  ชนิด  คือ

ชนิดขาว-ดำและชนิดสี  บริษัทมีความสามารถในการผลิตโทรทัศน์ทั้ง  2 ชนิดได้อย่างมาก  300  เครื่องต่อสัปดาห์  โดยเสียเงินในการผลิตโทรทัศน์ชนิดขาว-ดำ  เครื่องละ  3,600  บาท  และชนิดสีเครื่องละ  5,400  บาท  ทางบริษัทได้กำหนดจำนวนเงินในการผลิตโทรทัศน์ทั้งหมดไม่เกิน  1,296,000  บาท  ถ้าโทรทัศน์ชนิดขาว-ดำ  ขายได้กำไรเครื่องละ  1,800  บาท  และชนิดสีขายได้กำไรเครื่องละ  2,200  บาท  อยากทราบว่าบริษัทนี้ควรผลิตโทรทัศน์ชนิดขาว-ดำ  และชนิดสีอย่างละกี่เครื่องต่อสัปดาห์จึงจะได้กำไรมากที่สุดและได้กำไรเท่าใด

วิธีทำ        1.กําหนด               P แทนกำไรทั้งหมด

                                           x    แทนจำนวนการผลิตโทรทัศน์ชนิดขาว-ดำ  (เครื่อง/สัปดาห์)

                                           y   แทนจำนวนการผลิตโทรทัศน์ชนิดสี  (เครื่อง/สัปดาห์)

ชนิด   ของโทรทัศน์	ลงทุน   (บาท/เครื่อง)	กำไร   (บาท/อ่าง)	จำนวนที่ผลิต   (เครื่อง/สัปดาห์)
ขาว-ดำ	3,600	1,800	x ≥ 0
สี	5,400	2,200	y≥ 0

                2.สร้างฟังก์ชันจุดประสงค์ให้สอดคล้องกับที่โจทย์ต้องการ สร้างเงื่อนไขบังคับตามข้อมูลที่

โจทย์สั่ง  โดยเขียนแบบจำลองทางคณิตศาสตร์ 

                         สมการจุดประสงค์ คือ       P = 1,800x + 2,200y

                          อสมการข้อจำกัด                      x + y ≤  300

                                                        3,600x + 5,400y  ≤  1,269,000

                                                                                  x ≥ 0

                                                                                  y ≥ 0

                 

                   3.หาผลลัพธ์โดยวิธีที่ดีและง่ายที่สุดคือ การเขียนกราฟตามเงื่อนไขบังคับ เมื่อเขียนกราฟแล้ว ให้แรเงา อาณาบริเวณที่เป็นไปได้ 

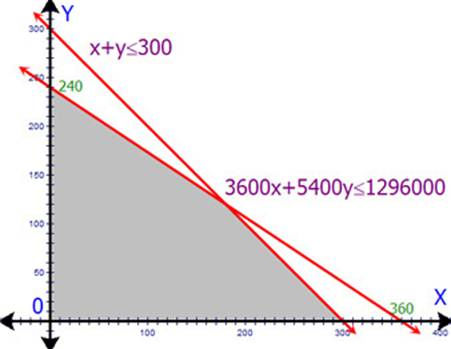
                   4.หาจุดยอดมุมทั้งหมดของบริเวณที่แรเงา

                                 คือ  (0 , 0) , (0 , 240) , (180 , 120) , (300 , 0)

                   5.นำแต่ละจุดไปแทนคำในฟังก์ชันเป้าหมาย จะได้ค่าสูงสุดหรือต่ำสุดตามต้องการ

                 

พิกัด (x,y)	P = 1,800x + 2,200y
(0,0)	P = 1,800(0) + 2,200(0)
(0,240)	P = 1,800(0) + 2,200(240) = 528,000
(180,240)	P = 1,800(180) + 2,200(120) = 588,000
(300,0)	P = 1,800(300) + 2,200(0) = 540,000

                       

                    จากตารางจะพบว่า ค่ามากที่สุดของ  P คือ  588,000  เมื่อ x = 180  y =  12

 

                    ดังนั้น  ในแต่ละสัปดาห์ควรผลิตโทรทัศน์ขาว-ดำ จำนวน  180  เครื่อง และผลิตโทรทัศน์สี จำนวน  120  เครื่อง จึงจะได้กำไร  588,000  บาท  ซึ่งเป็นกำไรที่มากที่สุด