ขยันอ่านสอบคณิตศาสตร์ รูปเรขาคณิตพื้นฐาน
เรขาคณิตพื้นฐาน
สี่เหลี่ยม คือ รูปร่างปิดที่มีมุมสี่มุมและด้านสี่ด้านเป็นขอบเขตสี่เหลี่ยมมีหลากหลายรูปแบบ ได้แก่
1. สี่เหลี่ยมผืนผ้า
2. สีเหลี่ยมจัตุรัส
3. สี่เหลี่ยมด้านขนาน
4. สี่เหลี่ยมรูปว่าว
5. สีเหลี่ยมขนมเปียกปูน
6. สี่เหลี่ยมคางหมู
เส้นขนาน คือ เส้นตรงหรือส่วนของเส้นตรงสองเส้นที่อยู่บนระนาบเดียวกัน จะขนานกันก็ต่อเมื่อเส้นตรงทั้งสองเส้นมีระยะห่างเท่ากัน และเมื่อมีเส้นตรงอีกเส้นมาตัดเส้นขนานทั้งสอง จะทำให้เกิดมุมแย้ง 2 แบบ คือ มุมแย้งภายใน และมุมแย้งภายนอก
สูตรการหาพื้นที่รูปสี่เหลี่ยมผืนผ้า
สูตร = กว้าง x ยาว
Ex.จงหาพื้นที่รูปสี่เหลี่ยมผืนผ้าที่มีด้านกว้าง 8 เซนติเมตร และ ด้านยาว 15 เซนติเมตร
สูตร = กว้าง x ยาว
= 8 x 15
= 90 ตารางเซนติเมตร
สูตรการหาพื้นที่รูปสี่เหลี่ยมจัตุรัส
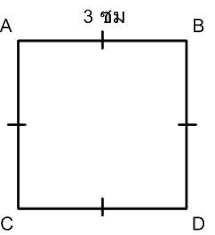
สูตร = ด้าน x ด้าน
EX. จงหาพื้นที่ของรูปสี่เหลี่ยมจัตุรัสที่มีความยาวด้านละ 3 เซนติเมตร
สูตร = ด้าน x ด้าน
= 3 x 3
= 9 ตารางเซนติเมตร

สูตร = 1/2 x ผลคูณของเส้นทะแยงมุม
Ex.จงหาพื้นที่รูปสี่เหลี่ยมขนมเปียกปูน ซึ่งเส้นAC ยาว 4 เซนติเมตร และ เส้นBD ยาว 3 เซนติเมตร
สูตร = 1/2 x ผลคูณของเส้นทะแยงมุม
= 1/2 x (3×4)
= 1/2 x12
= 6 ตารางเซนติเมตร
รูปเรขาคณิตสามมิติ
1.ปริซึม
ปริซึม เป็นรูปเรขาคณิตสามมิติที่มีหน้าตัด(ฐาน) ทั้งสองข้างเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการหน้าตัด (ฐาน) ทั้งสองอยู่ในระนาบที่ขนานกัน มีหน้าข้างเป็นรูปสี่เหลี่ยมมุมฉาก การเรียกชื่อปริซึมจะเรียกตามรูปหน้าตัดของปริซึมส่วนต่างๆของปริซึมมีชื่อเรียก ดังนี้
2.ทรงกระบอก
ทรงกระบอก เป็นรูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ ด้านข้างเป็นผิวเรียบโค้งส่วนต่างๆของทรงกระบอก
ทรงกระบอก เป็นรูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ ด้านข้างเป็นผิวเรียบโค้งส่วนต่างๆของทรงกระบอก
ข้อแตกต่างของปริซึมกับทรงกระบอก คือ
– ฐาน ปริซึมเป็นรูปหลายเหลี่ยมทรงกระบอกเป็นวงกลม- ด้านข้าง ปริซึมเป็นรูปสี่เหลี่ยมผืนผ้าทรงกระบอกเป็นผิวเรียบโค้ง
3.พีระมิด
พีระมิด เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยุ่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น การเรียกชื่อพีระมิดจะเรียกตามรูปฐานของพีระมิด
ส่วนต่างๆของพีระมิด
กรวย เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรงดด้านข้างเป็นผิวโค้งเรียบส่วนต่างๆของกรวย
ข้อแตกต่างของพีระมิดกับกรวย คือ- ฐาน พีระมิดฐานรูปหลายเหลี่ยมกรวยฐานรูปวงกลม
– ด้านข้าง พีระมิดเป็นรูปสามเหลี่ยมผืนผ้า
กรวยเป็นผิวเรียบโค้ง
5.ทรงกลม
ทรงกลม เป็น รูปเรขาคณิตสามมิติที่มีด้านข้างเป็นผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระยะเท่ากัน เรียกจุดคงที่ว่า จุดศูนย์กลางของทรงกลม เรียกระยะที่เท่ากันว่า รัศมีของทรงกลม ส่วนต่างๆของทรงกลม
รูปเรขาคณิตสองมิติ
| รูปเรขาคณิตสองมิติ แบ่งตามลักษณะของด้าน หรือ ขอบของรูปนั้น เช่น รูปสามเหลี่ยม |
| รูปสี่เหลี่ยม รูปหลายเหลี่ยม หรือ รูปวงกลม เป็นต้น ตัวอย่างรูปเรขาคณิตสองมิติ |
    |
| รูปสามเหลี่ยม รูปสี่เหลี่ยม รูปหลายเหลี่ยม รูปวงกลม |
| รูปเรขาคณิตสามมิติ เป็นรูปเรขาคณิตทรงสามมิติที่มีฐานหรือหน้าตัดเป็นรูปทรงต่างๆ เช่น |
| รูปทรงกระบอก รูปทรงกลม รูปพีระมิด รูปปริซึม รูปกรวย เป็นต้น ตัวอย่างรูปเรขาคณิตสามมิติ |
   |
| รูปทรงกระบอก รูปทรงกลม รูปพีระมิด รูปปริซึม |
รูปทรงเรขาคณิตแบบต่าง ๆ
รูปทรงกลม ลูกบอล แก้วน้ำ ภาชนะถ้วยชามต่าง ๆ ประกอบเป็นรูปร่างแบบต่าง ๆ ดังนั้นการจะอธิบายหรือออกแบบสิ่งต่าง ๆ จำเป็นต้องอาศัยทฤษฎีทางเรขาคณิต ปัจจุบันประเทศไทยกำลังจะมีรถไฟใต้ดิน ลองนึกดูว่า ถ้าจะเจาะอุโมงค์ จากที่หนึ่งให้ทะลุหรือชนกับการเจาะมาจากอีกแนวหนึ่งได้ ต้องใช้หลักการทางเรขาคณิตมาช่วย นักคณิตศาสตร์ เริ่มจากการกำหนดจุด จุดซึ่งไม่มีขนาด ไม่มีมิติ และถ้าเราให้จุดเคลื่อนที่แนวทางการเคลื่อนที่ของจุด ก่อให้เกิดเส้น หากหยิบแผ่นกระดาษมาหนึ่งแผ่น ผิวของแผ่นกระดาษเรียกว่าระนาบ รูปที่เกิดบนกระดาษนี้เรียกว่ารูประนาบ และถ้าดูที่ผิวของถ้วยแก้วที่เป็นรูปทรงกระบอก เราก็จะเห็นผิวโค้ง ซึ่งเราอาจมองรูปผิวโค้งของถ้วยแก้วในลักษณะสามมิติ












