คณิตศาสตร์พื้นฐาน ม.2
บทที่ 1 ทฤษฎีบทพีทาโกรัส
1.1 ทฤษฎีบทพีทาโกรัส
1.2 บทกลับของทฤษฎีบทพีทาโกรัส
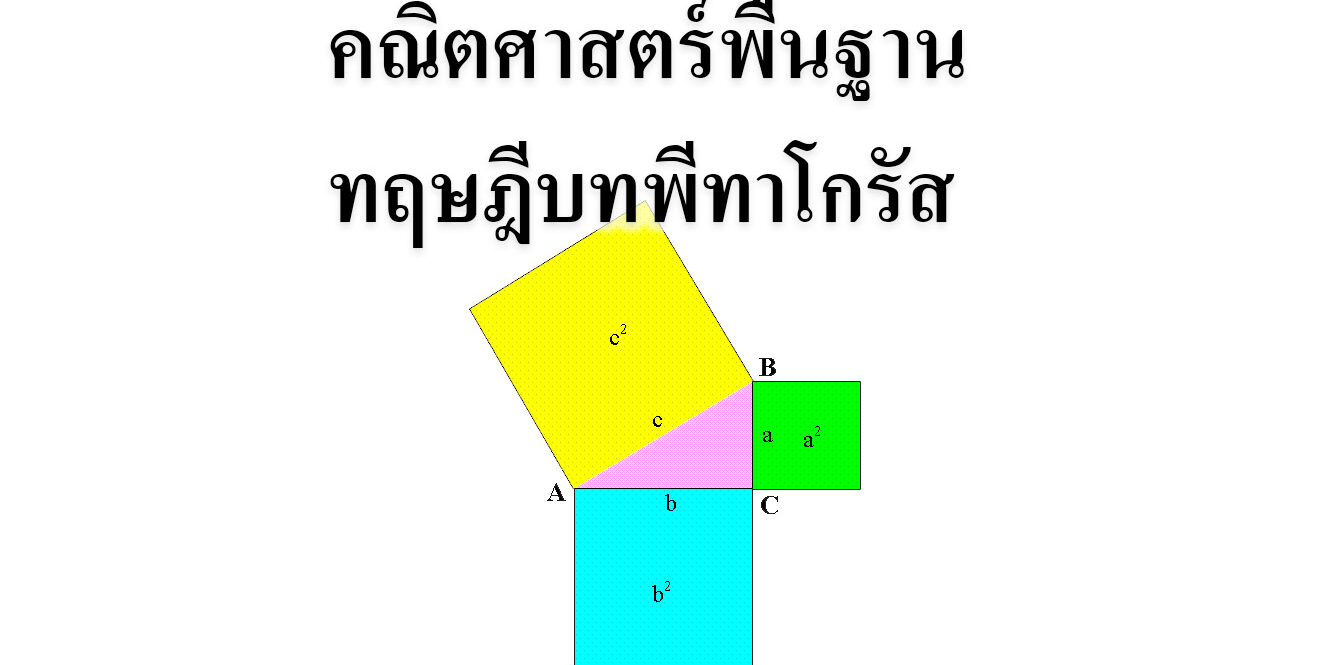
ทฤษฎีบทพีทาโกรัส คือ ทฤษฎีที่ว่าด้วยความสัมพันธ์ระหว่างด้านทั้งสามของรูปสามเหลี่ยมมุมฉาก
ซึ่งมีนิยามว่า “ในสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมฉากของสามเหลี่ยมมุมฉากนั้น”
จากรูปด้านบนน้องจะเห็นว่า พี่มีสามเหลี่ยมมุมฉากอยู่ 1 อันประกอบไปด้วยด้าน 3 ด้านได้แก่ a,b,c ซึ่งโดยปกติแล้ว เรานิยมแทน c เป็นด้านตรงข้ามมุมฉาก (ด้านที่ยาวสุดของสามเหลี่ยม) ส่วนด้าน a,b เนื่องจากมันติดกับมุมฉากเลย เราจึงเรียกสองด้านนี่ว่า ด้านประกอบมุมฉาก
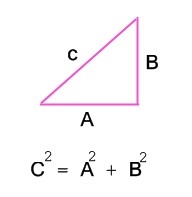
พีทาโกรัสกล่าวว่า ”ผลรวมของ(ด้านประกอบมุมฉากกำลังสอง) = ด้านตรงข้ามมุมฉากกำลังสอง” ซึ่งจากภาพด้านบนก็คือ a2+b2=c2 สมการนี้สมการเดียวเลยน้องที่ต้องจำ! เราเรียกมันว่า สูตรพีทาโกรัส
ตัวอย่างการใช้สมการทฤษฎีบทพีทาโกรัส
ทฤษฎีบทดังกล่าวสามารถเขียนเป็นสมการสัมพันธ์กับความยาวของด้าน a,b และ c ได้ ซึ่งมักเรียกว่า สมการพีทาโกรัส ซึ่งเขียนเป็นสมการได้ดังนี้
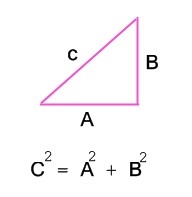
( อาจเขียนแทนด้วยตัวแปลอื่น เช่น x,y,z )
โดยที่ c เป็นความยาวด้านตรงข้ามมุมฉาก และ a,b เป็นความยาวของอีกสองด้านที่เหลือ
ทฤษฎีบทพีทาโกรัสตั้งตามชื่อนักคณิตศาสตร์ชาวกรีก พีทาโกรัส ซึ่งถือว่าเป็นผู้ค้นพบทฤษฎีบทและการพิสูจน์ แม้จะมีการแย้งบ่อยครั้งว่า ทฤษฎีบทดังกล่าวมีมาก่อนหน้าเขาแล้ว มีหลักฐานว่านักคณิตศาสตร์ชาวบาบิโลนเข้าใจสมการดังกล่าว แม้ว่าจะมีหลักฐานหลงเหลืออยู่น้อยมากว่าพวกเขาปรับให้มันพอดีกับกรอบคณิตศาสตร์
ทฤษฎีบทดังกล่าวเกี่ยวข้องกับทั้งพื้นที่และความยาว ทฤษฎีบทดังกล่าวสามารถสรุปได้หลายวิธี รวมทั้งปริภูมิมิติที่สูงขึ้น ไปจนถึงปริภูมิที่มิใช่แบบยูคลิด ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมมุมฉาก และอันที่จริงแล้ว ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมเลยก็มี แต่เป็นทรงตัน n มิติ ทฤษฎีบทพีทาโรัสดึงดูดความสนใจจากนักคณิตศาสตร์เป็นสัญลักษณ์ของความยากจะเข้าใจในคณิตศาสตร์ ความขลังหรือพลังปัญญา มีการอ้างถึงในวัฒนธรรมสมัยนิยมมากมายทั้งในวรรณกรรม ละคร ละครเพลง เพลง สแตมป์และการ์ตูน
กำหนด a, b และ c เป็นจำนวนจริงบวกที่จะมีสามเหลื่ยมมุมฉากหนึ่งรูปที่มีความยาวด้านเท่ากับสามจำนวนนั้น และสามเหลี่ยมนั้นจะมีมุมฉากระหว่างด้าน a และb
สำหรับสามเหลี่ยมใด ๆ ที่มีด้าน a, b และ c ถ้าแล้วมุมระหว่าง a กับ b จะวัดได้ 90°
ถ้าในสามเหลี่ยมรูปหนึ่ง สี่เหลี่ยมบนด้านหนึ่งเท่ากับผลรวมของสี่เหลี่ยมบนอีกสองด้านที่เหลือของสามเหลี่ยมแล้ว แล้วมุมที่รองรับด้านทั้งสองที่เหลือของสามเหลี่ยมนั้นจะเป็นมุมฉาก
- ถ้า
 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก - ถ้า
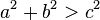 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม - ถ้า
 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน