ทฤษฎีบททวินาม
ในหัวข้อนี้จะกล่าวถึงสูตรของการกระจาย ( x + y )2 เมื่อ x, y เป็นจำนวนจริงใดๆ และ n เป็นจำนวนเต็มบวก
พิจารณาการกระจายต่อไปนี้
( x + y )1 = x + y
(x + y )2 = x2 + 2xy + y2
( x + y )3 = x3 +3x2 y + 3xy2 y3
( x + y )4 = x4 + 4x3 y + 6x2 y2 + 4xy3 + y4
(x + y )5 = x5 + 5x4 y + 10x3 y2 + 10x2 y3 +5xy4 + y5
พิจารณา (x + y )n = (x + y)(x + y)… ( x + y ) = n วงเล็บ
ในการกระจายเลือก x และ y อย่างใดอย่างหนึ่งของแต่ละวงเล็บนำมาคูณกันแล้วนำผลคูณ
ที่ได้มาบวกกัน เช่นเลือก y จาก 2 วงเล็บ และเลือก x จาก n – 2 วงเล็บที่เหลือจะได้พจน์ xn – 2 y2 ดังนั้น แต่ละพจน์ของการกระจาย ( x + y )n อยู่ในรูป xn – r yr เมื่อ r {0,1,2,…, n}
เนื่องจาก xn – r yr ประกอบด้วย x จำนวน n – r ตัว และ y จำนวน r ตัว ดังนั้น พจน์ xn – r yr มีทั้งหมด
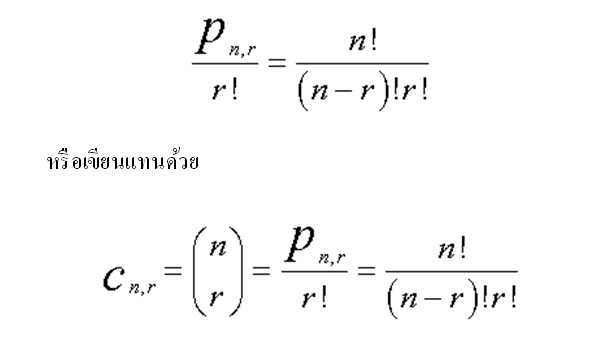
พจน์
นั่นคือ สัมประสิทธิ์ของ xn – r yr เท่ากับ
การกระจาย ( x + y )n สรุปเป็นทฤษฏีบทได้ดังนี้
ความน่าจะเป็นของเหตุการณ์ คือ จำนวนที่แสดงให้ทราบว่าเหตุการณ์ใดเหตุการณ์หนึ่ง มีโอกาสเกิดขึ้นมากหรือน้อยเพียงใด

|
อธิบายความได้ว่า 1. ความน่าจะเป็นของเหตุการณ์ที่เป็นไปได้ เป็น 0
2. ความน่าจะเป็นของเหตุการณ์ใดๆจะเป็นจำนวนใดจำนวนหนึ่ง
ตั้งแต่ 0 ถึง 1
|
แซมเปิลสเปซ(Sample Space) คือเซตของผลลัพธ์ที่อาจจะเกิดขึ้นได้ทั้งหมดจากการทดลองสุ่มและเป็นสิ่งที่เราสนใจ เรานิยมใช้สัญลักษณ์ S แทนแซมเปิลสเปซ จากความหมายของแซมเปิลสเปซ แสดงว่า ในการทดลองหรือการกระทำใด ๆ ก็ตาม ผลลัพธ์ที่มีโอกาสจะเกิดขึ้นได้ต้องเป็นสมาชิกในแซมเปิลสเปซทั้งสิ้น
ผลลัพธ์ที่อาจจะเกิดขึ้นได้คือ หัว หรือ ก้อย
ดังนั้น แซมเปิลสเปซที่ได้ คือ S = {หัว, ก้อย}
ผลลัพธ์ที่อาจจะเกิดขึ้นได้คือ ลูกเต๋าขึ้นแต้ม 1 หรือ 2 หรือ 3 หรือ 4 หรือ 5 หรือ 6
ดังนั้นแซมเปิลสเปซที่ได้คือS = {1, 2,3,4,5,6}
ตัวอย่างที่ 3 จากการทดลองสุ่มโดยการทดลองทอดลูกเต๋า 2 ลูก
1. จงหาแซมเปิลสเปซของแต้มของลูกเต๋าที่หงายขึ้น
2. จงหาแซมเปิลสเปซของผลรวมของแต้มบนลูกเต๋า
ดังนั้นเราต้องเขียนแต้มของลูกเต๋าที่มีโอกาสที่จะหงายขึ้นมาทั้งหมด
และเพื่อความสะดวกให้ (a,b) แทนผลลัพธ์ที่อาจจะเกิดขึ้น โดยที่
a แทนแต้มที่หงายขึ้นของลูกเต๋าลูกแรก
b แทนแต้มที่หงายขึ้นของลูกเต๋าลูกที่สอง
ดังนั้นแซมเปิลสเปซของการทดลองสุ่มคือ
S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
ดังนั้นเราต้องเขียนผลรวมของแต้มบนลูกเต๋าที่มีโอกาสเกิดขึ้นได้ทั้งหมด
จะได้แซมเปิลสเปซของผลรวมของแต้มบนลูกเต๋าทั้ง 2 ลูก คือ {2,3,4,5,6,7,8,9,10,11,12}
ตัวอย่างที่ 4 ในกล่องใบหนึ่งมีลูกบอลสีแดง 2 ลูก สีขาว 1 ลูก ถ้าเราหยิบลูกบอลออกจากกล่องมา 1 ลูก โดยวิธีสุ่ม
1. จงหาแซมเปิลสเปซของสีของลูกบอลที่จะเกิดขึ้น
2. จงหาแซมเปิลสเปซของลูกบอลที่หยิบออกมาได้
ดังนั้นแซมเปิลสเปซของสีของลูกบอลที่หยิบได้คือ S= {สีแดง,สีขาว}
2. เนื่องจากโจทย์สนใจลูกบอลที่จะหยิบมาได้ ซึ่งมีทั้งหมด 3 ลูก
สมมติให้เป็น แดง1 แดง2 ขาว1
ดังนั้นแซมเปลิสเปซของลูกบอลที่หยิบออกมาคือ S = {แดง1,แดง2, ขาว1}
2. เหตุการณ์ที่ได้แต้มที่หารด้วย 2 ลงตัว ( E2 )
3. เหตุการณ์ที่ได้แต้มคี่ ( E2 )
1. แซมเปิลสเปส (S) คือ { 20 < X < 50} เมื่อ X เป็นค่าหนึ่ง ๆ
2. เหตุการณ์ที่นักศึกษาได้น้อยกว่า 30
3. เหตุการณ์ที่นักศึกษาได้คะแนนสูงกว่า 40
วิธีจัดหมู่
วิธีจัดหมู่ คือ วิธีการจัดสิ่งของที่แตกต่างกันออกเป็นกลุ่ม หรือ หมู่โดย
ไม่คำนึงถึงอันดับ เช่น การจัดหมู่ตัวอักษร A , B และ C ออกเป็นหมู่ละ 2 ตัวอักษร
จะจัดได้ AB AC และ BC เพียง 3 หมู่ หรือ 3 วิธี
จะเห็นว่า AB และ BA เป็นหมู่เดียวกัน หรือAC กับ CA เป็นหมู่เดียวกัน หรือ
BC กับ CBเป็นหมู่เดียวกัน ดั้งนั้นการจัดหมู่ไม่ใช่การจัดลำดับ
จำนวนวิธีจัดหมู่ของ n สิ่งที่แตกต่างกัน โดยนำมาจัดหมู่คราวละ r สิ่ง ( r < n ) เท่ากับ
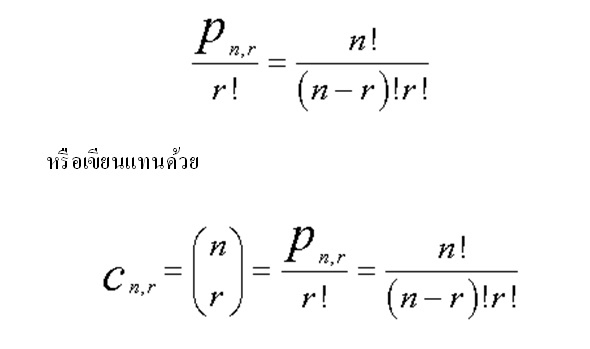
ตัวอย่างที่ 1 ชาย 6 คน และหญิง 6 คน ในจำนวนนี้มีนายสมบัติ และนางสาวสมศรี รวมอยู่ด้วย ถ้าให้ผู้ชายไปจับคู่กับผู้หญิง
จะมีวิธีการจับคู่กี่วิธี เมื่อ
(1) ไม่มีเงื่อนไขใดเพิ่มเติม
(2) นายสมบัติจับคู่กับนางสาวสมศรี
(3) นายสมบัติไม่จับคู่กับนางสาวสมศรี
วิธีทำ (1) จำนวนวิธีการจับคู่ = จำนวนวิธีเรียงสับเปลี่ยนของชาย 6 คน (หรือของหญิง 6 คน)
= 6! = 720 วิธี
(2) จำนวนวิธีของการจับคู่โดยสมบัติจับคู่กับสมศรี = 1×5! = 120 วิธี
(3) จำนวนวิธีของการจับคู่โดยสมบัติไม่จับคู่กับสมศรี = 5×5! = 600 วิธี
(หรือเท่ากับ 720 – 120 = 600 วิธี)
ตัวอย่างที่2 มีครูชาย 2 คน ครูหญิง 2 คน นักเรียนชาย 2 คน และนักเรียนหญิง 2 คน มายืนเรียงแถวยาว จะมีวิธีการยืน
ทั้งหมดกี่วิธี เมื่อ
(1) ครูชายยืนติดกัน ครูหญิงยืนติดกัน แต่ครูชายและครูหญิงยืนไม่ติดกัน
(2) ครูชาย ครูหญิง นักเรียนชาย และนักเรียนหญิง ยืนสลับกันทีละคน โดยที่ลำดับต้องเหมือนกับ
ลำดับของชุดแรก
(3) ครูชาย ครูหญิง ยืนสลับกันทีละคน และนักเรียนชาย นักเรียนหญิง ยืนสลับกันทีละคน
วิธีทำ (1) นักเรียนชาย 2 คน และนักเรียนหญิง 2 คน มีวิธีการยืน = 4! = 24 วิธี
มีช่องว่าง 5 ช่อง รวมครูชาย 2 คน เป็น 1 คน และรวมครูหญิง 2 คน เป็น 1 คน
นำครูชายและครูหญิงไปแทรก จำนวนวิธีการแทรก = 5P2 × 2! × 2!
= 5! / 3! ×4 = 80 วิธี
ดังนั้น จำนวนวิธีการยืน = 24 × 80 = 1,920 วิธี
(2) จำนวนวิธีเรียงสับเปลี่ยนของชุดแรก = 4! = 24 วิธี
ในแต่ละวิธี ครูชาย ครูหญิง นักเรียนชาย และนักเรียนหญิงมีการสลับกันเองได้
2! × 2! ×2! ×2! = 16 วิธี
ดังนั้น จำนวนวิธีการยืน = 241 ×6 = 384 วิธี
(3) จำนวนวิธีการยืนของครูชาย และครูหญิงโดยยืนสลับกันทีละคน เท่ากับ
2! × 2! ×2 ! = 8 วิธี
จำนวนวิธีการยืนของนักเรียนชาย และนักเรียนหญิงโดยยืนสลับกันทีละคน เท่ากับ
2! × 2! ×2 ! = 8 วิธี
จำนวนวิธีเรียงสับเปลี่ยนของกลุ่มครูและกลุ่มนักเรียน = 2! = 2 วิธี
ดั้งนั้น จำนวนวิธีการยืน = 8×8×2 = 128 วิธี
ตัวอย่างที่ 3 ถ้าต้องการสลับตัวอักษรในคำว่า PREFACE จะสลับได้กี่วิธี เมื่อต้องการให้อักษรที่ซ้ำกันอยู่ติดกัน และ
(1) ไม่มีเงื่อนไขใดเพิ่มเติม (4) ขึ้นต้นด้วยพยัญชนะ
(2) อักษรที่ซ้ำกันอยู่ริม (5) ขึ้นต้นด้วยสระ
(3) อักษรที่ซ้ำกันต้องไม่อยู่ริม (6) พยัญชนะอยู่ติดกัน
วิธีทำ (1) จำนวนวิธีสลับ = 6! = 720 วิธี
(2) ตัวอักษร EE อยู่ริม มีวิธีการสลับ = 2 วิธี
ตัวอักษร 5 ตัวที่เหลือ = 5! = 120 วิธี
ดังนั้น จำนวนวิธีการสลับ = 2 ×120 = 240 วิธี
(3) ตัวอักษร EE มีวิธีการสลับตำแหน่ง 4 วิธี (ยกเว้นหัวและท้าย)
ตัวอักษร 5 ตัวที่เหลือ = 5! = 120 วิธี
ดังนั้น จำนวนวิธีการสลับ = 4 ×120 = 480 วิธี
(4) พยัญชนะ ได้แก่ P, R, F, C
จำนวนวิธีการนำตัวอักษรใส่ในตำแหน่งแรก = 4 วิธี
จำนวนวิธีสลับตัวอักษร 5 ตัว = 5! = 120 วิธี
ดังนั้น จำนวนวิธีการสลับ = 4 ×120 = 480 วิธี
(5) กรณีที่ 1 ขึ้นต้นด้วย EE
จำนวนวิธีการสลับ = 1 ×5! = 120 วิธี
กรณีที่ 2 ขึ้นต้นด้วย A
จำนวนวิธีการสลับ = 1 ×5! = 120 วิธี
ดังนั้น จำนวนวิธีการสลับ = 120 + 120 = 240 วิธี
PRFC E
E A
(6) จำนวนวิธีสลับ = 3!× 4! = 6× 24 = 144 วิธี
วิธีเรียงสับเปลี่ยน
1. วิธีการเรียงสับเปลี่ยนสิ่งของที่แตกต่างกันทั้งหมด
หมายถึง การนำสิ่งของที่มีลักษณะที่แตกต่างกันทั้งหมดมาจัดเรียงสับเปลี่ยน โดยถือตำแหน่งหรือลำดับก่อนหลังเป็นสำคัญ แบ่งออกเป็น 3 แบบ คือ
1) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนวเส้นเดียวกัน (แต่ไม่เป็นวงกลม) เท่ากับ n! วิธี
2) จำนวนวิธีเรียงสับเปลี่ยนสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนวเส้นเดียวกัน โดยจัดทีละ r สิ่ง (r £ n) เท่ากับ n! / (n-r)! วิธี
* เขียนแทนด้วย P(n, r) = n! / (n-r)!
จาก P(n, r) = n! / (n-r)!
= n . (n-1) . (n-2) . … . (n-r+1) . (n-r)! / (n-r)!
= n . (n-1) . (n-2) . … . (n-r+1)
3) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลม เท่ากับ (n-1)! วิธี และมีหลักการจัดเรียง โดยแบ่งตามเงื่อนไขได้ดังนี้
3.1 การจัดสิ่งของ n สิ่ง วึ่งแตกต่างกันทั้งหมดในแนววงกลม โดยไม่มีเงื่อนไข จะจัดได้เท่ากับ (n-1)! วิธี
3.2 การสร้างจุดอ้างอิงบนวงกลมก่อน แล้วแทรกเข้าไป วนเป็นวงกลม โดยที่รู้ว่ามีจุดอ้างอิงก่อนแล้ว
3.3 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลม โดยที่มีเงื่อนไขการสับที่ แล้วแทรกอีกฝ่ายหนึ่งเข้าในฝ่ายแรก โดยต้องรู้ว่าการแทรกครั้งนี้มีจุดอ้างอิงแล้ว
3.4 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลม โดยจัดทีละ r สิ่ง (r £ n) เท่ากับ n! / (n-r)! . r! วิธี
* เขียนแทนด้วย [P(n, r)] / r = n! / (n-r)! . r!
3.5 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลมแบบมองได้ 2 ด้าน (แบบสามมิติ)
3.6 การจัดสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดในแนววงกลมแบบมองได้ 2 ด้าน โดยจัดทีละ r สิ่ง (r £ n)
* เขียนแทนด้วย [P(n, r)] / 2r = n! / (n-r)! . 2r!
ตัวอย่างที่ 1 จะสร้างเลข 4 หลัก จากตัวเลข 1, 2, 3, 4 ได้กี่จำนวน
วิธีทำ จากโจทย์ ตรงตามข้อที่ 1
จะได้ว่า จะสร้างตัวเลข 4 หลัก ได้ = 4! = 4 . 3 . 2 . 1 = 24
ดังนั้น จะสร้างตัวเลข 4 หลัก ได้ 24 จำนวน
ตัวอย่างที่ 2 จะสร้างเลข 2 หลัก จากตัวเลข 1, 2, 3, 4, 5 ได้กี่จำนวน
วิธีทำ จากโจทย์ ตรงตามข้อที่ 2
จะได้ว่า จะสร้างตัวเลข 2 หลัก ได้ = P(5,2) = 5! / (5-2)! = 5! / 3! = 5 . 4 = 20
ดังนั้น จะสร้างตัวเลข 2 หลัก ได้ 20 จำนวน
ตัวอย่างที่ 3 เลือกนักเรียน 3 คน จากนักเรียนทั้งหมด 20 คน มาเป็นหัวหน้าห้อง รองหัวหน้าห้อง และเลขานุการ ได้ทั้งหมดกี่วิธี
วิธีทำ จากโจทย์ ตรงตามข้อที่ 2
จะได้ว่า จะได้วิธีที่เลือก = P(20,3) = 20! / (20-3)! = 20! / 17! = 20 . 19 . 18 = 6840
ดังนั้น จำนวนวิธีที่เลือก คือ 6840 วิธี
ตัวอย่างที่ 4 จัดเด็ก 1 คน หญิง 3 คน และผู้ชาย 3 คน นั่งรอบโต๊ะกลม โดยที่ผู้ชายไม่นั่งติดกับเด็ก จะจัดได้กี่วิธี
วิธีทำ จากโจทย์ ตรงตามข้อที่ 3.2 ซึ่งผู้ชายไม่นั่งติดกับเด็ก แสดงว่าด้านซ้ายและด้านขวาของเด็กจะต้องถูกประกบด้วยผู้หญิง
ขั้นที่ 1 นำเด็กมาวนเป็นหลักก่อน จะสามารถทำได้ (1-1)! = 0! = 1 วิธี
ขั้นที่ 2 นำผู้หญิงมาประกบด้านซ้ายและด้านขวาของเด็ก จะมำได้ P(3,2) = 3! / (3-2)! = 3 . 2 = 6 วิธี
ขั้นที่ 3 นำผู้ชาย 3 คน กับผู้หญิง 1 คนที่เหลือ มาจัด จะทำได้ 4! = 4 . 3 . 2 . 1 =24 วิธี
ฉะนั้น จำนวนวิธีที่จัดได้ทั้งหมด คือ 1 . 6 . 24 = 144 วิธี
ดังนั้น จัดได้ทั้งหมด 144 วิธี
2. วิธีการเรียงสับเปลี่ยนสิ่งของที่ไม่แตกต่างกันทั้งหมด
จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่ง ซึ่งซ้ำกันบางส่วน ดังนี้
กลุ่มที่ 1 มีสิ่งของที่มีความซ้ำกันอยู่ n1 สิ่ง
กลุ่มที่ 2 มีสิ่งของที่มีความซ้ำกันอยู่ n2 สิ่ง
กลุ่มที่ 3 มีสิ่งของที่มีความซ้ำกันอยู่ n3 สิ่ง
.
.
.
กลุ่มที่ k มีสิ่งของที่มีความซ้ำกันอยู่ nk สิ่ง
เมื่อ n = n1 + n2 + n3 + … + nk
1) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของทั้ง n สิ่ง ซึ่งไม่แตกต่างกันทั้งหมดในแนวเส้นตรง คือ
[n! / n1! . n2! . n3! . … . nk!] วิธี
2) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของทั้ง n สิ่ง ซึ่งไม่แตกต่างกันทั้งหมดในแนวเส้นตรง โดยจัดทีละ r สิ่ง (r)
3) จำนวนวิธีเรียงสับเปลี่ยนของสิ่งของทั้ง n สิ่ง ซึ่งไม่แตกต่างกันทั้งหมดในแนวเส้นตรง โดยที่ ห.ร.ม. ของ n1, n2, n3, … , nk = 1 คือ [(n-1)! / n1! . n2! . n3! . … . nk!] วิธี
ตัวอย่างที่ 1 ต้องการนำตัวอักษรทั้งหมดจากคำว่า “CHAKKARIN” มาจัดเรียงเป็นวงกลม จะทำได้กี่วิธี
วิธีทำ ตรงตามข้อ 3
คำว่า CHAKKARIN มี A 2 ตัว, K 2 ตัว และ C, H, R, I, N อย่างละ 1 ตัว
ห.ร.ม. ของ 2, 2, 1, 1, 1, 1, 1 คือ 1 ซึ่งใช้สูตรในการหาจำนวนวิธีได้
ดังนั้น วิธีจัดเรียงเป็นวงกลมได้ทั้งหมด 9! / 2! . 2! . 1! . 1! . 1! . 1! . 1! วิธี
ตัวอย่างที่ 2 จงหาจำนวนวิธีที่จะจัดพนักงาน 6 คน เป็น 3 กลุ่มแบ่งไปทำงาน 3 งานที่แตกต่างกัน โดยจัดกลุ่มละกี่คนก็ได้
วิธีทำ ตรงตามข้อ 1
ลองแจกแจงรูปแบบของการจัดกลุ่มทั้งหมด โดยการแยกเป็นกรณีย่อยตามโจทย์ได้ 10 แบบ ดังนี้
123, 132, 213, 231, 312, 321, 114, 141, 411, 222
กรณี 1 พบว่า 6 แบบแรก เป็นการจัดพนักงาน 6 คน เป็น 3 กลุ่ม กลุ่มละ 1, 2 และ 3
แสดงว่า 6 แบบแรกจะมีวิธีการแบ่งเท่ากับ 6! / 1! . 2! . 3! = 60 วิธี
กรณี 2 พบว่า แบบที่ 7-9 เป็นการจัดพนักงาน 6 คน เป็น 3 กลุ่ม กลุ่มละ 1, 1 และ 4
แสดงว่า แบบที่ 7-9 จะมีวิธีการแบ่งเท่ากับ 6! / 1! . 1! . 4! = 30 วิธี
กรณี 3 พบว่า แบบที่ 10 เป็นการจัดพนักงาน 6 คน เป็น 3 กลุ่ม กลุ่มละ 2, 2 และ 2
แสดงว่า แบบที่ 10 จะมีวิธีการแบ่งเท่ากับ 6! / 2! . 2! . 2! = 90 วิธี
ดังนั้น จำนวนวิธีทั้งหมดที่จะจัดพนักงาน 6 คน เป็น 3 กลุ่มเท่ากับ 6(60) + 3(30) + (1)90 = 540 วิธี







