คณิตศาสตร์ ความน่าจะเป็น สรุปทฤษฎีบททวินาม

ทฤษฎีบททวินาม
ในหัวข้อนี้จะกล่าวถึงสูตรของการกระจาย ( x + y )² เมื่อ x, y เป็นจำนวนจริงใดๆ และ n เป็นจำนวนเต็มบวก

       พิจารณาการกระจายต่อไปนี้
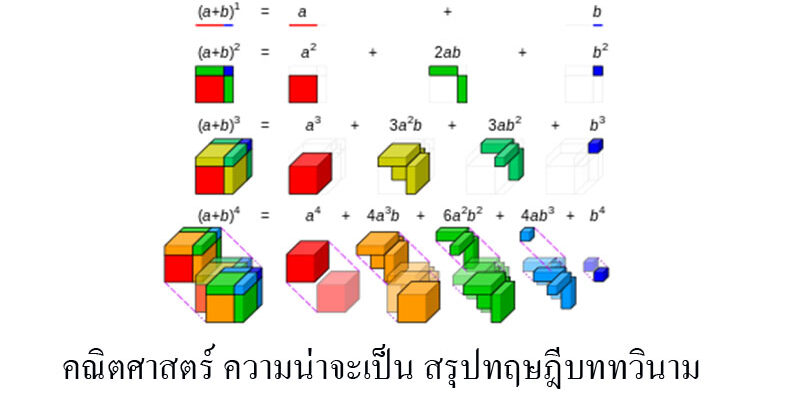
            ( x + y )¹      =   x + y
(x + y )²       =   x² + 2xy + y²
( x + y )³      =   x³ +3x² y + 3xy²  y³
( x + y )⁴      =   x⁴ + 4x³ y + 6x² y²  + 4xy³  + y⁴
(x  + y )⁵      =   x⁵ + 5x⁴ y + 10x³ y² + 10x² y³ +5xy⁴ + y⁵
พิจารณา  (x + y )ⁿ   =   (x + y)(x + y)… ( x  +  y )    =    n  วงเล็บ
ในการกระจายเลือก x  และ y อย่างใดอย่างหนึ่งของแต่ละวงเล็บนำมาคูณกันแล้วนำผลคูณ
ที่ได้มาบวกกัน เช่นเลือก  y  จาก 2 วงเล็บ และเลือก  x  จาก  n – 2  วงเล็บที่เหลือจะได้พจน์   x^{n – 2} y²   ดังนั้น แต่ละพจน์ของการกระจาย  ( x + y )ⁿ  อยู่ในรูป x^{n – r}y^r   เมื่อ  r     {0,1,2,…, n}
เนื่องจาก   x^{n – r} y^r   ประกอบด้วย   x   จำนวน  n – r  ตัว  และ  y  จำนวน  r  ตัว ดังนั้น  พจน์  x^{n – r} y^r   มีทั้งหมด

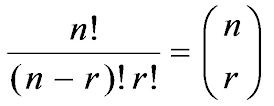
พจน์
นั่นคือ สัมประสิทธิ์ของ x^{n – r} y^r เท่ากับ
การกระจาย ( x + y )ⁿ สรุปเป็นทฤษฏีบทได้ดังนี้

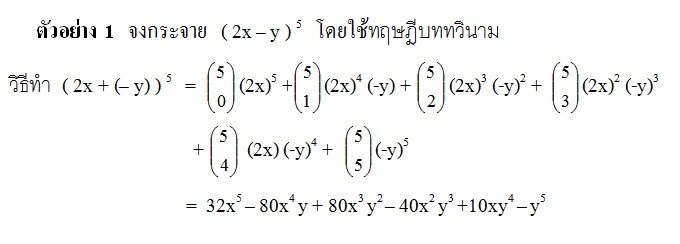
ในการกระจาย ( x + y )ⁿ เมื่อ n {0,1,2,…} สัมประสิทธิ์ของแต่ละพจน์แสดงได้ดังนี้

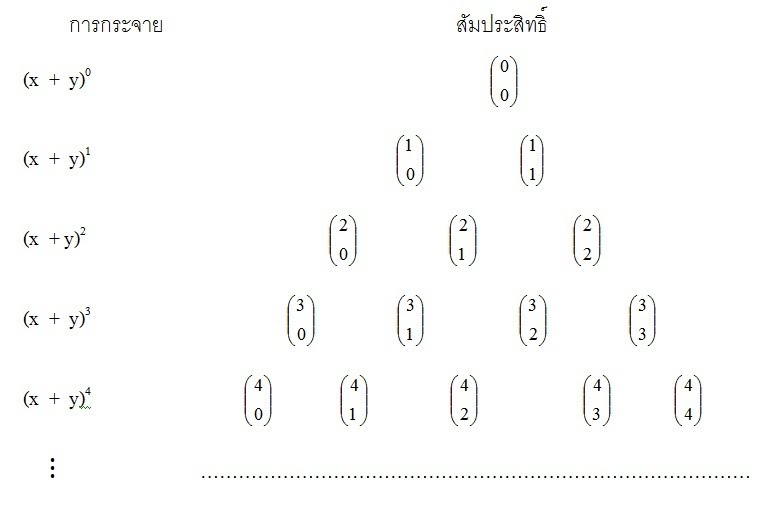
ดังนั้น  การกระจาย     (x  +  y)⁴   สามารถหาสัมประสิทธิ์ของพจน์ ต่าง ๆ ได้   โดยกูจากแถวที่  5
ของรูปสามเหลี่ยมปาสกาล   ซึ่งจะได้ว่า
                               ( x + y )⁴      =   x⁴ + 4x³ y + 6x² y²  + 4xy³  + y⁴

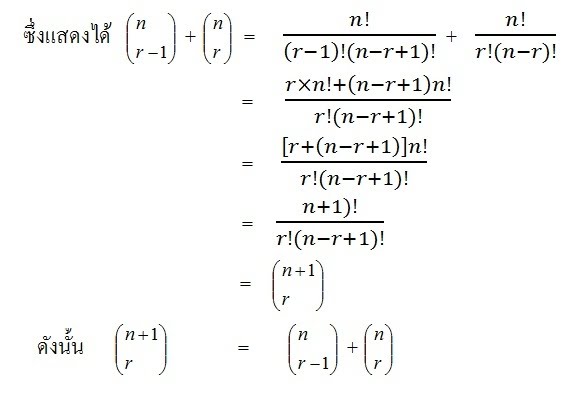
ความน่าจะเป็น

ทฤษฎีบททวินามที่เกี่ยวข้องอย่างใกล้ชิดกับมวลฟังก์ชันของการกระจายทวินามเชิงลบ ความน่าจะเป็นของการรวบรวม (นับได้) ของการทดลอง Bernoulli อิสระ $\{X_{t}\}_{t\in S}$ กับความน่าจะเป็นของความสำเร็จ $p\in [0,1]$ ทั้งหมดไม่ได้เกิดขึ้นคือ

P\left(\bigcap _{t\in S}X_{t}^{C}\right)=(1-p)^{|S|}=\sum _{n=0}^{|S|}{|S| \choose n}(-p)^{n}.

ขอบเขตบนที่เป็นประโยชน์สำหรับปริมาณนี้คือ $e^{-p|S|}.$ ⁽²⁰⁾

ในพีชคณิตนามธรรม

ทฤษฎีบททวินามที่ถูกต้องมากขึ้นโดยทั่วไปสำหรับสององค์ประกอบ

x

และ

y ที่

ในแหวนหรือแม้กระทั่งsemiringโดยมีเงื่อนไขว่า

XY =

ตัวอย่างเช่น มันถือสอง

n \times n

เมทริกซ์ โดยมีเงื่อนไขว่าเมทริกซ์เหล่านั้นทด; สิ่งนี้มีประโยชน์ในการคำนวณกำลังของเมทริกซ์ ^[21]

ทฤษฎีบททวินามสามารถที่ระบุไว้โดยบอกว่าลำดับพหุนาม ${1, x, x 2, x 3, \dots }$ เป็นประเภททวินาม

ในวัฒนธรรมสมัยนิยม

ทฤษฎีบททวินามที่ถูกกล่าวถึงในหลักทั่วไปของเพลงในละครตลกโจรสลัดที่เพนแซน
ศาสตราจารย์ Moriartyอธิบายโดย Sherlock Holmes ว่ามีการเขียนตำราเกี่ยวกับทฤษฎีบททวินาม
กวีชาวโปรตุเกสFernando Pessoaใช้ชื่ออื่นÁlvaro de Camposเขียนว่า “ทวินามของนิวตันนั้นสวยงามพอ ๆ กับVenus de Miloความจริงก็คือมีคนเพียงไม่กี่คนที่สังเกตเห็น” ^[22]
ในภาพยนตร์เรื่องThe Imitation Gameปี 2014 อลัน ทัวริงกล่าวถึงงานของไอแซก นิวตันเกี่ยวกับทฤษฎีบททวินามระหว่างที่เขาพบกับผู้บัญชาการเดนนิสตันครั้งแรกที่ Bletchley Park