ความรู้เบื้องต้นเกี่ยวกับจำนวนจริงคณิตศาสตร์ ม.2
จุดประสงค์หัวข้อ
นักเรียนสามารถ
1. เขียนเศษส่วนให้อยู่ในรูปทศนิยมซ้ำ
2. เขียนทศนิยมซ้ำ ให้อยู่ในรูปเศษส่วน
3. บอกได้ว่าจํานวนที่กําหนดให้เป็นจํานวนตรรกยะหรือไม่
4. ยกตัวอย่างจํานวนตรรกยะได้
5. ตระหนักถึงความสมเหตุสมผลของคําตอบที่ได้
ทศนิยม
คือ จำนวนจริงที่มีเครื่องหมาย . (จุดทศนิยม) วางอยู่ระหว่างจำนวนเต็ม เช่น 1.22, 0.347, 3.0, -3.60 เป็นต้น
ประเภทของทศนิยมมี 2 ประเภท คือ ทศนิยมซ้ำ กับ ทศนิยมไม่ซ้ำ (ในที่นี้จะกล่าวถึงแต่ทศนิยมซ้ำ)
ทศนิยมซ้ำ
ทศนิยมซ้ำแบ่งเป็น 2 แบบ ดังนี้
1. ทศนิยมซ้ำแบบรู้จบ คือ รู้แน่นอนว่าตัวไหนซ้ำและซ้ำกี่ตัว เช่น 2.1, 3.5, 5.75, 8.125 เป็นต้น
2. ทศนิยมซ้ำแบบไม่รู้จบ คือ รู้แน่นอนว่าตัวไหนซ้ำ แต่ไม่รู้ว่าซ้ำกี่ตัว เช่น 1.1212…, 0.345345…, 3.111111…, 4.521212121… เป็นต้น
เขียนทศนิยมซ้ำ ให้อยู่ในรูปเศษส่วน หรือ การแปลงทศนิยมซ้ำเป็นเศษส่วน
ทศนิยมที่ไม่ใช่ทศนิยมซ้ำเราสามารถแปลงเป็นเศษส่วนได้ ตัวอย่าง เช่น
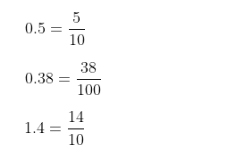
ในทำนองเดียวกันถ้าเรามีทศนิยมซ้ำเราก็สามารถที่จะแปลงเป็นเศษส่วนได้เช่นเดียวกัน ซึ่งมีวิธีการแปลงดังต่อไปนี้
ตัวอย่างที่ 1 จงแปลง ให้อยู่ในรูปเศษส่วน

นั่นคือ สามารถเขียนเป็นเศษส่วนได้คือ
บอกได้ว่าจํานวนที่กําหนดให้เป็นจํานวนตรรกยะหรือไม่
จำนวนตรรกยะและอตรรกยะ
จำนวนตรรกยะ
ในทางคณิตศาสตร์, จำนวนตรรกยะ (หรือเศษส่วน) คืออัตราส่วนของจำนวนเต็มสองจำนวน มักเขียนอยู่ในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็ม และ b ไม่เท่ากับศูนย์
จำนวนตรรกยะแต่ละจำนวนสามารถเขียนได้ในรูปแบบที่หลากหลาย ตัวอย่างเช่น 3 / 6 = 2 / 4 = 1 / 2 รูปแบบที่เรียกว่า เศษส่วนอย่างต่ำ a และ b นั้น a และ b จะต้องไม่มีตัวหารร่วม และจำนวนตรรกยะทุกจำนวนสามารถเขียนได้ในรูปเศษส่วนอย่างต่ำนี้
ทศนิยม เป็นรูปแบบที่แผ่ขยายออกมา และต่อเนื่องไปเรื่อยๆ อย่างไม่มีที่สิ้นสุด (ยกเว้นกรณีซ้ำศูนย์ เราสามารถละ โดยไม่ต้องเขียนได้) ข้อความนี้เป็นจริงสำหรับจำนวนตรรกยะทุกจำนวน
จำนวนจริงที่ไม่ใช่จำนวนตรรกยะ เรียกว่า จำนวนอตรรกยะ
แผนภูมิจำนวนจริง
1. จำนวนอตรรกยะ หมายถึง จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือทศนิยมซ้ำได้ ตัวอย่างเช่น √2 , √3, √5, -√2, – √3, -√5 หรือ ¶ ซึ่งมีค่า 3.14159265…
2. จำนวนตรรกยะ หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ ตัวอย่างเช่น
• ระบบจำนวนตรรกยะ
จำนวนตรรกยะยังสามารถแบ่งเป็น 2 ประเภท คือ
1. จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนหรือทศนิยมซ้ำได้ แต่ไม่เป็นจำนวนเต็ม ตัวอย่างเช่น
2. จำนวนเต็ม หมายถึง จำนวนที่เป็นสมาชิกของเซต I = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …} เมื่อกำหนดให้ I เป็นเซตของจำนวนเต็ม
• ระบบจำนวนเต็ม
จำนวนเต็มยังสามารถแบ่งได้อีกเป็น 3 ประเภทด้วยกัน
1. จำนวนเต็มลบ หมายถึง จำนวนที่เป็นสมาชิกของเซต I – โดยที่
I – = {…, -4, -3, -2, -1}
เมื่อ I – เป็นเซตของจำนวนเต็มลบ
2. จำนวนเต็มศูนย์ (0)
3. จำนวนเต็มบวก หมายถึง จำนวนที่เป็นสมาชิกของเซต I+ โดยที่
I+ = {1, 2, 3, 4, …}
เมื่อ I+ เป็นเซตของจำนวนเต็มบวก
จำนวนเต็มบวก เรียกได้อีกอย่างว่า “จำนวนนับ” ซึ่งเขียนแทนเซตของจำนวนนับได้ด้วยสัญลักษณ์ N โดยที่
N = I+ = {1, 2, 3, 4, …}
ในทางคณิตศาสตร์ “…ตรรกยะ” หมายถึง เราจำกัดขอบเขตให้อยู่ในระบบจำนวนตรรกยะเท่านั้น เช่น พหุนามตรรกยะ
เซตของจำนวนตรรกยะทั้งหมดเราใช้สัญลักษณ์ Q หรือตัวใหญ่บนกระดานดำ โดยใช้เซตเงื่อนไข ได้ดังนี้
จำนวนตรรกยะ หมายถึง จำนวนที่เขียนแทนในรูปเศษส่วน เมื่อ a และ b เป็นจำนวนเต็ม และ
ตัวอย่างจำนวนที่เป็นจำนวนตรรกยะ เช่น จำนวนเต็ม , เศษส่วน , ทศนิยมซ้ำ เป็นต้น
จํานวนตรรกยะและจํานวนอตรรกยะ
จำนวนตรรกยะและอตรรกยะ
จำนวนตรรกยะ

1. จำนวนอตรรกยะ หมายถึง จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือทศนิยมซ้ำได้ ตัวอย่างเช่น √2 , √3, √5, -√2, – √3, -√5 หรือ ¶ ซึ่งมีค่า 3.14159265…
2. จำนวนตรรกยะ หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ ตัวอย่างเช่น
• ระบบจำนวนตรรกยะ
จำนวนตรรกยะยังสามารถแบ่งเป็น 2 ประเภท คือ
1. จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนหรือทศนิยมซ้ำได้ แต่ไม่เป็นจำนวนเต็ม ตัวอย่างเช่น
2. จำนวนเต็ม หมายถึง จำนวนที่เป็นสมาชิกของเซต I = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …} เมื่อกำหนดให้ I เป็นเซตของจำนวนเต็ม
• ระบบจำนวนเต็ม
จำนวนเต็มยังสามารถแบ่งได้อีกเป็น 3 ประเภทด้วยกัน
1. จำนวนเต็มลบ หมายถึง จำนวนที่เป็นสมาชิกของเซต I – โดยที่
I – = {…, -4, -3, -2, -1}
เมื่อ I – เป็นเซตของจำนวนเต็มลบ
2. จำนวนเต็มศูนย์ (0)
3. จำนวนเต็มบวก หมายถึง จำนวนที่เป็นสมาชิกของเซต I+ โดยที่
I+ = {1, 2, 3, 4, …}
เมื่อ I+ เป็นเซตของจำนวนเต็มบวก
จำนวนเต็มบวก เรียกได้อีกอย่างว่า “จำนวนนับ” ซึ่งเขียนแทนเซตของจำนวนนับได้ด้วยสัญลักษณ์ N โดยที่
N = I+ = {1, 2, 3, 4, …}
ในทางคณิตศาสตร์ “…ตรรกยะ” หมายถึง เราจำกัดขอบเขตให้อยู่ในระบบจำนวนตรรกยะเท่านั้น เช่น พหุนามตรรกยะ
เซตของจำนวนตรรกยะทั้งหมดเราใช้สัญลักษณ์ Q หรือตัวใหญ่บนกระดานดำ โดยใช้เซตเงื่อนไข ได้ดังนี้
จำนวนตรรกยะ หมายถึง จำนวนที่เขียนแทนในรูปเศษส่วน เมื่อ a และ b เป็นจำนวนเต็ม และ
ตัวอย่างจำนวนที่เป็นจำนวนตรรกยะ เช่น จำนวนเต็ม , เศษส่วน , ทศนิยมซ้ำ เป็นต้น
การแก้โจทย์ปัญหาเกี่ยวกับสมการเชิงเส้นตัวแปรเดียว และตระหนักถึงความสมเหตุสมผลของคำตอบที่ได้
ในบทที่แล้วเราได้เรียนรู้เกี่ยวกับการเขียนสมการเชิงเส้นตัวแปรเดียวแทนสถานการณ์หรือปัญหา ดังนั้นบทนี้เรามาแก้สมการที่ได้จากปัญหา เพื่อหาคำตอบกันครับ แล้วจากนั้นเราจะนำคำตอบที่ได้ไปตรวจสอบกันว่าถูกต้องและสมเหตุสมผลหรือไม่
ตัวอย่างการแก้ปัญหาและตรวจสอบความสมเหตุสมผลที่ได้กันครับ
โจทย์ ฉันมีปากกาอยู่ 5 แท่ง ฉันมีดินสออยู่ 7 แท่ง ฉันมีดินสอกับปากการวมกันกี่แท่ง วิธีทำ
เราจะได้สมการเป็น 5 + 7 = x
ดังนั้น x = 12
ซึ่ง x ในที่นี้ก็คือ ดินสอกับปากการวมกัน
ตรวจคำตอบ มีดินสอ 5 แท่ง ปากกา 7 แท่ง ดังนั้นมีดินสอกับปากการวมกันเป็น 7 + 5 = 12 ซึ่งก็ตรงกับคำตอบของ x
โจทย์ อีก 5 ปี มาลีจะมีอายุ 27 ปี ดังนั้นตอนนี้มาลีมีอายุกี่ปี
วิธีทำ
เราจะได้สมการเป็น x + 5 = 27
ดังนั้น x = 22
ซึ่ง x ในที่นี้คือ ตอนนี้มาลีอายุเท่าไหร่
ตรวจคำตอบ ตอนนี้มาลีอายุ 22 ปีอีก 5 ปีมาลีอายุ 27 ปี ดังนั้นตอนนี้มาลีอายุ 22 ปีสมเหตุสมผลกับคำตอบ






