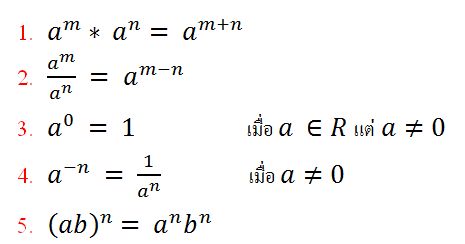เนื้อหาคณิตศาสตร์มัธยมศึกษาตอนต้น
คณิตศาสตร์ พื้นฐาน ม.ต้น
คณิตศาสตร์ พื้นฐาน ม.1 หลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551 สำหรับน้องๆที่ต้องการศึกษาหาความรู้เพิ่มเติม เทคนิค และสูตรสำหรับการเรียน การสอบ และการประยุกต์ใช้ต่างๆ
บทที่ 1 จำนวนเต็ม
จำนวนเต็ม
บทที่ 2 การสร้างทางเรขาคณิต
จุด เส้น และเส้นขนาน
บทที่ 3 เลขยกกำลัง
สรุปสุตรเลขยกกำลัง
บทที่ 4 ทศนิยมและเศษส่วน
เศษส่วน
ทศนิยม
บทที่ 5 รูปเรขาคณิตสองมิติและสามมิติ
มิติและสามมิติ
พื้นที่
ปริมาตร
จำนวนเต็ม (Integer)
จำนวนเต็ม คือ จำนวนที่ไม่มีเศษส่วนและทศนิยมรวมอยู่ในจำนวนนั้น
จำนวนเต็มประกอบด้วย
1. จำนวนเต็มบวก ได้แก่ 1 , 2 , 3 , 4 , 5 , 6 , …
2. จำนวนเต็มลบ ได้แก่ … , -4 , -3 , -2 , -1
3. ศูนย์ ได้แก่ 0
จำนวนเต็มบวก หรือ จำนวนนับ
จำนวนเต็มบวก หรือ จำนวนนับ คือ จำนวนเต็มที่มีค่ามากกว่า 0 ไปเรื่อย ๆโดยที่ไม่สามารถระบุได้
ว่าจำนวนนับตัวสุดท้ายเป็นอะไร จำนวนนับเริ่มต้นที่ 1 , 2 , 3, … ซึ่งเราทราบแล้วว่า จำนวนนับที่น้อยที่สุด คือ 1 จำนวน
นับที่มากที่สุดหาไม่ได้ คุณสมบัติของศูนย์และหนึ่ง
จำนวนเต็มลบ
จำนวนเต็มลบ คือ จำนวนที่มีค่าน้อยกว่า ศูนย์ มีตำแหน่งอยู่ทางด้านซ้ายมือของศูนย์เมื่ออยู่บนเส้นจำนวน
และ จะมีค่าลดลงเรื่อย ๆ โดยไม่สามารถจะบอกได้ว่าจำนวนใดจะมีค่าน้อยที่สุด แต่เราสามารถรู้ได้ว่าจำนวนเต็มลบ
ที่มีค่ามากที่สุด คือ -1 เราพอจะสรุปลักษณะที่สำคัญของจำนวนเต็มลบได้ดังนี้
1. จำนวนเต็มลบเป็นจำนวนที่มีค่าน้อยกว่าศูนย์ หรือถ้ามองบนเส้นจำนวนก็คือ เป็นจำนวนที่อยู่ทางซ้ายมือของศูนย์
2. จำนวนเต็มลบที่มีน้อยที่สุดไม่สามารถหาได้ แต่ จำนวนเต็มลบที่มีค่ามากที่สุด คือ -1
3. ตัวเลขที่ตามหลังเครื่องหมายลบ ถ้ายิ่งมีค่ามากขึ้นจำนวนเต็มลบนั้นจะมีค่าน้อยลงกล่าวคือ …-5 < -4 < -3 < -2 < -1
ศูนย์ ( ใช้สัญลักษณ์ “0” )
ศูนย์ ( ใช้สัญลักษณ์ “0” ) เป็นจำนวนเต็มอีกชนิดหนึ่ง ที่เราไม่ถือว่าเป็นจำนวนนับจากหลักฐานที่ค้นพบทำให้เราทราบ
ว่ามนุษย์รู้จักใช้สัญลักษณ์ “0” ในราวปีค.ศ. 800 โดยที่ “0” แทนปริมาณของการไม่มีของหรือของที่ต้องการกล่าวถึงแต่ก็ไม่ใช่ว่า 0
จะไม่มีความหมายถึงการไม่มีเสมอไป ตัวอย่างเช่น ระดับผลการเรียนทางด้านความรู้ โดยนักเรียนที่มีระดับผลการเรียนเป็น 0
ไม่ได้หมายความว่านักเรียนคนนั้นไม่มีความรู้ เพียงแต่ ว่ามีความรู้ในระดับหนึ่งเท่านั้น
เส้นจำนวน
เส้นจำนวน แสดงได้ดังนี้แบ่งแต่ละช่องให้เท่ากัน จะแบ่งกี่ช่องก็ได้ขึ้นอยู่กับจำนวนเต็ม ที่ต้องการในการเขียนเส้นจำนวน
เขียนหัวลูกศรทั้งสองข้างเพื่อแสดงว่ายังมีจำนวนอื่นๆ ที่มากกว่าหรือน้อยกว่าจำนวนที่เขียนแสดงไว้
จุด เส้น และเส้นขนาน
นักเรียนสามารถ
1. สร้างเส้นตั้งฉากตามที่กำหนดได้ 2. สร้างเส้นขนานตามที่กำหนดได้
บทเรียน
การสร้างเส้นตั้งฉาก
1. การสร้างเส้นตั้งฉากที่จุด ๆ หนึ่งบนเส้นตรงที่กำหนดให้
การสร้างเส้นตั้งฉากที่จุด ๆ หนึ่งบนเส้นตรงที่กำหนดให้จะเหมือนกับการสร้างมุม 90 นั่นเอง
2. การสร้างเส้นตั้งฉากจากจุด ๆ หนึ่งที่อยู่ภายนอกเส้นตรงมายังเส้นตรงที่กำหนดให้
ให้พิจารณาตัวอย่างต่อไปนี้ในตารางด้านล่าง
จงลากเส้นตั้งฉากจาก จุด Q มายัง (RS)
ที่กำหนดให้ ขั้นตอนการสร้าง
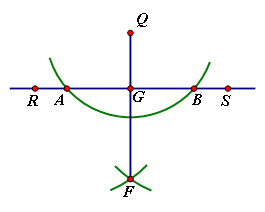
ใช้จุด Q เป็นจุดศูนย์กลาง รัศมียาวพอสมควรเขียนส่วนโค้งตัด (RS) ที่จุด A และ จุด B
ใช้จุด A และ จุด B เป็นจุดศูนย์กลาง รัศมียาวพอสมควร เขียนส่วนโค้งตัดกันที่จุด F
ลาก (QF) ตัด (RS) ที่จุด G
จะได้ว่า (QF) ตั้งฉากกับ (RS) ที่จุด G ตามที่ต้องการ
การสร้างเส้นขนาน
** เส้นตรงสองเส้นจะขนานกัน ก็ต่อเมื่อ เส้นตรงทั้งสองเส้นนั้นมีระยะห่างที่เท่ากันเสมอ **
บทนิยาม ถ้าเส้นตรงเส้นหนึ่งตัดกับเส้นตรงคู่หนึ่ง ทำให้มุมแย้งมีขนาดเท่ากันแล้วเส้นตรงคู่นั่นจะขนานกัน
การสร้างเส้นตรงให้ผ่านจุดจุดหนึ่งและขนานกับเส้นตรงที่กำหนด ให้พิจารณาตัวอย่างต่อไปนี้
จงสร้าง (EF) //(GH) ขั้นตอนการสร้าง

สร้างจุด B บน (EF) กางวงเวียนให้รัศมียาวพอประมาณ เขียนส่วนโค้งตัด (EF) ที่จุด N และใช้จุด N เป็นจุดศูนย์กลาง เขียนส่วนโค้งตัดกับส่วนโค้งแรก ที่จุด O
ลาก (BA) กางวงเวียนให้รัศมียาวเท่ากับข้อ 1 ใช้จุด A เป็นจุดศูนย์กลาง เขียนส่วนโค้งให้ตัดกับ (BA) ที่จุด P และ ใช้จุด P เป็นจุดศูนย์กลาง เขียนส่วนโค้งให้ตัดกับส่วนโค้งแรกที่จุด Q
ลาก (GH) ผ่านจุด Q และ A
จะได้ว่า (EF) //(GH) เนื่องจาก มุม QAP = มุม NBO ตามบทนิยาม
ประเด็นสำคัญ
การสร้างเส้นตั้งฉากมุมที่ได้มีขนาดเท่ากับ 90๐
การสร้างเส้นขนานอาศัยจาก บทนิยาม ที่ว่า ถ้าเส้นตรงเส้นหนึ่งตัดกับเส้นตรงคู่หนึ่ง ทำให้มุมแย้งมีขนาดเท่ากันแล้วเส้นตรงคู่นั่นจะขนานกัน และ เส้นตรงสองเส้นจะขนานกัน ก็ต่อเมื่อ เส้นทั้งสองเส้นนั้นมีระยะห่างที่เท่ากันเสมอ
เลขยกกำลัง
ถ้าจำนวนที่คูณตัวเองซ้ำกันหลาย ๆ ตัว เราจะเขียนจำนวนเหล่านั้นออกมาในรูปของเลขยกกำลัง โดยจำนวนที่คูณตัวเองซ้ำ ๆ จะเรียกว่า “ฐาน” และจำนวนตัวที่คูณ จะเรียกว่า “เลขชี้กำลัง” เพื่อให้เข้าใจมากยิ่งขึ้น เพื่อน ๆ ลองนึกถึงการพับกระดาษ 1 แผ่น
พับกระดาษ 1 ครั้ง กระดาษถูกแบ่งออกเป็น 2 ส่วน
พับกระดาษ 2 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 = 4 ส่วน
พับกระดาษ 3 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 x 2 = 8 ส่วน
พับกระดาษ 10 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1,024 ส่วน
กระดาษพับซ้อนกัน 1,024 ทบนี่หนามาก ๆ เลย และในชีวิตจริง ถ้าต้องเขียน 2 x 2 x 2 x … x 2 ให้ครบตามต้องการก็คงจะเหนื่อยและเสียเวลามาก ๆ นักคณิตศาสตร์จึงนิยมเขียนออกมาในรูปของ “เลขยกกำลัง” ซึ่งประกอบไปด้วยฐานและเลขชี้กำลัง เราสามารถเขียน 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 ให้อยู่ในรูปเลขยกกำลังได้ว่า 210 ซึ่ง 2 คือฐาน และ 10 คือเลขชี้กำลัง และจะอ่าน 210 ว่า…
2 กำลัง 10
2 ยกกำลัง 10
หรือ กำลัง 10 ของ 2
เลขยกกำลัง ฐาน และเลขชี้กำลัง
จำนวนที่สามารถเป็นฐานได้มีหลายรูปแบบ เช่น จำนวนเต็มบวก จำนวนเต็มลบ เศษส่วน ทศนิยม ยกตัวอย่างเช่น 24 (-2)4 (![]() )2 0.45
)2 0.45
ข้อสังเกต: อ่านไม่เหมือนกัน ผลลัพธ์ไม่เท่ากัน
ลบสองทั้งหมดยกกำลังสี่
(-2)4 = (-2)(-2)(-2)(-2) = 16
ลบสองยกกำลังสี่
-24 = – (2 x 2 x 2 x 2) = -16
จะเห็นว่า (-2)4 มีค่าไม่เท่ากับ -24 แค่ใส่วงเล็บ ผลลัพธ์ก็ต่างกันแล้ว ดังนั้นเพื่อน ๆ ต้องระวังการใส่วงเล็บให้ดีนะ เราลองมาดูตัวอย่างอื่น ๆ เพิ่มกันดีกว่า
54 = 5 x 5 x 5 x 5 = 625
(5)4 = (5)(5)(5)(5) = 625
-54 = -(5 x 5 x 5 x 5) = -(625) = -625
(-5)4 = (-5)(-5)(-5)(-5) = (25)(25) = 625
กรณีนี้ เลขชี้กำลังเป็นจำนวนคู่ สำหรับฐานที่เป็นจำนวนลบ จะเห็นว่า (-5)4 เท่ากับ 54 แต่ไม่เท่ากับ -54 อย่าลืมสังเกตให้ดีนะว่าเครื่องหมายลบอยู่ข้างในหรือข้างนอกวงเล็บ
53 = 5 x 5 x 5 = 125
-53 = -(5 x 5 x 5) = -125
(-5)3 = (-5)(-5)(-5) = -125
กรณีนี้ เลขชี้กำลังเป็นจำนวนคี่ สำหรับฐานที่เป็นจำนวนลบ จะเห็นว่า (-5)3 เท่ากับ -53 แต่ (-5)3 ไม่เท่ากับ 53
*ข้อสังเกต*
ถ้าฐานเป็นจำนวนลบ เลขชี้กำลังเป็นจำนวนคี่ > ได้ผลลัพธ์เป็นจำนวนลบ
ถ้าฐานเป็นจำนวนลบ เลขชี้กำลังเป็นจำนวนคู่ > ได้ผลลัพธ์เป็นจำนวนบวก
จากตัวอย่างที่ผ่านมา เราสามารถสรุปเป็นตารางได้ว่า
| ฐานเลขชี้กำลัง | เลขชี้กำลัง | ||
| จำนวนคี่ | จำนวนคู่ | ||
| ฐาน | จำนวนบวก | ผลลัพธ์เป็นจำนวนบวก | ผลลัพธ์เป็นจำนวนบวก |
| จำนวนลบ | ผลลัพธ์เป็นจำนวนลบ | ผลลัพธ์เป็นจำนวนบวก | |
แต่เพื่อน ๆ ก็ต้องสังเกตให้ดีด้วยนะว่าเครื่องหมายลบอยู่ในวงเล็บหรือนอกวงเล็บ แถมบางครั้งโจทย์ก็มีเครื่องหมายลบซ้อนสองชั้นทั้งในและนอกวงเล็บด้วย สังเกตดี ๆ นะจะได้ไม่พลาด
กรณีเลขชี้กำลัง n เป็นจำนวนเต็มบวก
กรณีเลขชี้กำลังเป็นศูนย์หรือจำนวนเต็มลบ เมื่อฐาน a≠0
กรณีเลขชี้กำลังเป็นเศษส่วน
สมบัติเลขยกกำลัง
สูตรผลคูณ-ผลหารของเลขยกกำลังฐานเดียวกัน
กรณีกำลังซ้อนกันสองชั้นขึ้นไปโดยไม่มีวงเล็บ ให้คำนวณจากบนลงล่าง เหมือนกับสูตรที่สอง
สูตรกระจายกำลังเข้าไปในผลคูณ-ผลหาร
สูตรกระจายกำลังเข้าไปในราก
การจัดรูปเลขยกกำลัง
การจัดรูปเลขยกกำลัง มีจุดประสงค์เพื่อจัดให้เลขยกกำลังของเราอยู่ในรูปอย่างง่าย
รูปอย่างง่ายของเลขยกกำลัง หมายถึงเลขยกกำลังที่
- เลขชี้กำลังทุกตัวเป็นบวก
- รวมเลขยกกำลังที่มีฐานเดียวกันเอาไว้ด้วยกัน
ทศนิยมและเศษส่วน
ทศนิยม
ทศนิยมได้ถูกนำมาใช้ในชีวิตประจำวันอย่างกว้างขวาง เช่น การวัดความยาว อุณหภูมิของอากาศ การคิดราคาสินค้า การคิดภาษี เป็นต้น ทั้งนี้ เนื่องจากการใช้หน่วยที่เป็นจำนวนเต็มนั้นไม่เพียงพอ ยังมีปริมาณที่เป็นเศษของหน่วยหรือไม่เต็มหน่วย จึงต้องมีระบบการเขียนตัวเลขแทนปริมาณเหล่านั้น ที่เรียกว่า ระบบทศนิยม ซึ่งตกลงกันเป็นสากลให้ใช้ จุด ” . ” เรียกว่า “จุดทศนิยม” คั่นระหว่างจำนวนเต็มกับ เศษของหน่วย
การอ่านทศนิยม
การอ่านทศนิยม ตัวเลขหน้าจุดทศนิยมอ่านแบบจำนวนเต็ม ตัวเลขหลังจุดทศนิยมอ่านเรียงตัว เช่น
3.125 อ่านว่า สามจุดหนึ่งสองห้า
0.02 อ่านว่า ศูนย์จุดศูนย์สอง
305.50 อ่านว่า สามร้อยห้าจุดห้าศูนย์
ค่าของตัวเลขตามค่าประจำหลัก
ตัวอย่าง 784.126
7อยู่ในหลักร้อย
มีค่าเป็น 700
8อยู่ในหลักสิบ
มีค่าเป็น 80
4อยู่ในหลักหน่วย
มีค่าเป็น 4
1อยู่ในหลักส่วนสิบ
มีค่าเป็น หรือ 0.1
2อยู่ในหลักส่วนร้อย
มีค่าเป็น หรือ 0.02
6อยู่ในหลักส่วนพัน
มีค่าเป็น หรือ 0.006
การทำทศนิยมให้เป็นเศษส่วน
ทศนิยมสามารถนำมาเขียนเป็นเศษส่วนที่มีตัวส่วนเป็น 10 100 1000 ….. ได้ และเศษส่วนจำนวนใดก็ตามที่สามารถทำให้ตัวส่วนเป็น 10 100 1000 ……. ได้ ย่อมสามารถเขียนให้อยู่ในรูปทศนิยมได้เช่นกัน
การทำเศษส่วนให้เป็นทศนิยม
เศษส่วนสามารถนำมาเขียนเป็นทศนิยมจากที่มีตัวส่วนเป็น 10 100 1000 ….. ได้ และเศษส่วนจำนวนใดก็ตามที่สามารถทำให้ตัวส่วน เป็น 10 100 1000 …….ได้ ย่อมสามารถเขียนให อยู่ในรูปทศนิยมได้เช่นกัน
การบวก ลบทศนิยม
การบวกและการลบทศนิยม เป็นการนำจำนวนที่อยู่ในหลักเดียวกันมาบวก หรือลบกัน ด้วยวิธีการอย่างเดียวกับการบวกและการลบของ จำนวนนับ โดยจำนวนที่อยู่ในตำแหน่งเดียวกันจะต้องตรงกันและจุดทศนิยมจะต้องตรงกันด้วย
การคูณ การหารทศนิยม
การคูณทศนิยม
การคูณจำนวนนับกับทศนิยมคล้ายกับการคูณจำนวนนับกับจำนวนนับ แต่จำนวนตำแหน่งของทศนิยมจะเท่ากับจำนวนตำแหน่งของทศนิยมของจำนวนที่มาคูณ
การหาผลคูณระหว่างทศนิยมกับ 10 100 1000….. ใช้หลักการคูณเช่นเดัยวกับการหาผลคูณระหว่างจำนวนนับ กับ 10 100 1000….. โดยใส่จุดทศนิยมให้มีจำนวนตำแหน่งเท่ากับจำนวน ตำแหน่งของทศนิยมที่กำหนดให้
การคูณทศนิยมด้วยจำนวนนับจะได้ผลคูณเป็นทศนิยมที่มีจำนวนตำแหน่งเท่ากับจำนวนตำแหน่งของ ทศนิยมที่กำหนดให้
ผลคูณของการคูณทศนิยมกับทศนิยมเหมือนกับการคูณจำนวนนับกับจำนวนนับ แต่ต้องใส่จุดทศนิยม เพื่อแสดง จำนวนตำแหน่งทศนิยมของผลคูณ ซึ่งจะเท่ากับผลบวกของจำนวนตำแหน่ง ของทศนิยมทั้งสองที่นำมาคูณกัน
การหารทศนิยมด้วยจำนวนนับ
ตำแหน่งของจุดทศนิยมของผลหารจะอยู่ตรงกับตำแหน่งของจุดทศนิยมของตัวตั้งเสมอ ในการหารที่มีตัวหารเป็นทศนิยม สามารถทำตัวหารให้เป็นจำนวนเต็มได้ โดยการใช้วิธีการคูณทศนิยมด้วย 10 100 1000 ……. ทั้งนี้ขึ้นอยู่กับจำนวนตำแหน่งของทศนิยมตัวหาร ตัวหารเป็นทศนิยม 1 ตำแหน่ง ต้องคูณตัวหารด้วย 10 ถ้าตัวหารเป็นทศนิยม 2 ตำแหน่ง ต้องคูณตัวหารด้วย 100 เป็นต้น
เศษส่วน
เศษส่วน หมายถึง ตัวเลขหรือสัญลักษณ์แทนจำนวนที่ไม่ใช่จำนวนเต็ม เศษส่วนจะประกอบด้วยตัวเศษและตัวส่วน
เศษส่วนมี 3 ชนิด คือ
1.เศษส่วนแท้ ได้แก่เศษส่วนที่ค่าของตัวเศษน้อยกว่าตัวส่วน
2.เศษส่วนเกิน ได้แก่ เศษส่วนที่ค่าของตัวเศษมากกว่าตัวส่วน
3.เศษส่วนจำนวนคละ ได้แก่ เศษส่วนที่มีจำนวนเต็มรวมกับเศษส่วนแท้
การทำเศษส่วนแท้ให้เป็นเศษส่วนอย่างต่ำ ทำโดยการนำจำนวนที่หารทั้งเศษและส่วนลงตัว เช่น ทำเป็นเศษส่วนอย่างต่ำได้ หรือ ทำเป็นเศษส่วนอย่างต่ำได้
การทำเศษส่วนเกินให้เป็นเศษส่วนจำนวนคละ โดยนำตัวส่วนหารตัวเศษ หารจนไม่สามารถหารได้ จะได้ผลลัพธ์เป็นจำนวนเต็ม รวมกับเศษส่วนที่เหลือ
การทำเศษส่วนจำนวนคละให้เป็นเศษส่วนเกิน โดยการนำตัวส่วนคูณกับจำนวนเต็มและบวกด้วยตัวเศษ
รูปเรขาคณิตสองมิติและสามมิติ
รูปเรขาคณิตสามมิติ เป็นรูปเรขาคณิตทรงสามมิติที่มีฐานหรือหน้าตัดเป็นรูปทรงต่างๆ เช่น รูปทรงกระบอก รูปทรงกลม รูปพีระมิด รูปปริซึม รูปกรวย เป็นต้น ตัวอย่างรูปเรขาคณิตสามมิติ ลองมาพิจารณารูปเรขาคณิต 2 มิติ และ 3 มิติ ดังนี้
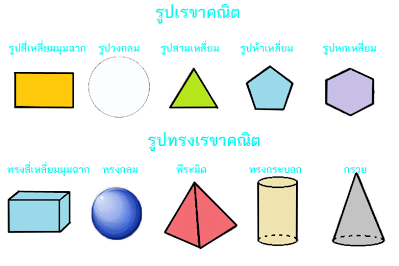
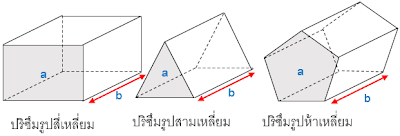
ปริซึม(Prism) เป็นรูปเรขาคณิตสามมิติที่มีฐานทั้งสองเป็นรูปเหลี่ยมที่เท่ากันทุกประการ ฐานทั้งสองอยู่บนระนาบที่ขนานกัน และด้านข้างแต่ละด้านเป็นรูปสี่เหลี่ยมด้านขนาน เรียกว่า ปริซึม
คุณสมบัติของปริซึม
– รูปทรงสามมิติที่มีหน้าตัดหัวท้ายเป็นรูปเหลี่ยม
– พื้นที่หน้าตัดหัวท้ายมีขนาดเท่ากัน
– ด้านข้างของรูปทรงสามมิติเป็นรูปสี่เหลี่ยมทุกรูป
– ชื่อเรียกของปริซึมเรียกตามรูปพื้นที่หน้าตัด เช่น ปริซึมรูปสามเหลี่ยม ปริซึมรูปสี่เหลียม ปริซึมรูปห้าเหลี่ยม เป็นต้น
ทรงกระบอก(Cylinder) คือ รูปทรงเรขาคณิต 3 มิติที่มีพื้นที่ฐานเป็นวงกลมทั้งสองด้าน
คุณสมบัติของทรงกระบอก
– รูปทรงสามมิติที่มีฐานเป็นรูปวงกลมทั้งสองด้าน
– เมื่อตัดรูปทรงสามมิตินี้ในระนาบที่ขนานกับฐาน จะได้รอยตัดเป็นรูปวงกลม
– เมื่อตัดรูปทรงสามมิตินี้ในระนาบที่ตั้งฉากกับฐาน จะได้รอยตัดเป็นรูปสี่เหลี่ยม
พีระมิด(Pyramid)คือ รูปทรงเรขาคณิต 3 มิติที่มีพื้นที่ฐานเป็นรูปหลายเหลี่ยม (สามเหลี่ยม สี่เหลี่ยม ห้าเหลี่ยม ….. รูป n เหลี่ยม) และมียอดเป็นจุดยอดแหลม
คุณสมบัติของพีระมิด
– รูปทรงสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ
– มียอดแหลม และไม่อยู่ในระนาบเดียวกับฐาน
– ด้านข้างของรูปทรงสามมิติเป็นรูปสามเหลี่ยมทุกรูป
– ชื่อเรียกของปริซึมเรียกตามรูปหน้าตัดฐาน เช่น พีระมิดฐานสามเหลี่ยม พีระมิดฐานสี่เหลียม พีระมิดฐานห้าเหลี่ยม เป็นต้น

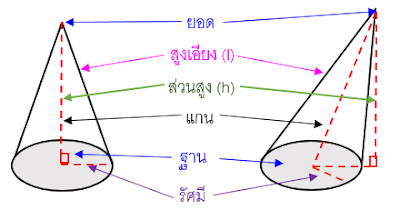
ทรงกรวย (cone) คือ รูปทรงในเรขาคณิต3 มิติ ที่มีรูปร่างเป็นกรวย ส่วนปลายด้านหนึ่งจะแหลม ที่อยู่ต่อกันระหว่างจุดยอดและจุดใดๆบนขอบฐานเป็นส่วนเส้นตรงที่เรียกว่า สูงเอียง
คุณสมบัติของทรงกรวย
– รูปทรงสามมิติที่มีฐานเป็นรูปวงกลม
– มียอดเป็นมุมแหลม
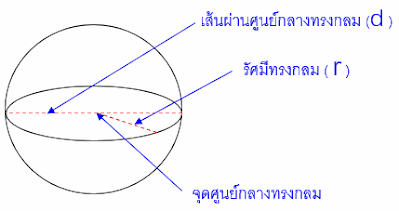
ทรงกลม (Sphere)
คุณสมบัติของทรงกลม
– รูปทรงสามมิติที่มีรูปทรงเป็นทรงกลม
– จุดทุกจุดบนพื้นผิวทรงกลมจะมีระยะห่างจากจุดศูนย์กลางเท่ากันเสมอ