คณิตศาสตร์ ม.1 เรื่องจำนวนเต็ม
จำนวนเต็ม ม.1
จำนวนเต็มคืออะไร
จำนวนเต็ม คือ จำนวนที่ไม่มีเศษส่วนและทศนิยมรวมอยู่ในจำนวนนั้น ซึ่งจำนวนเต็มจะแบ่งออกเป็น 3 แบบคือ
1. จำนวนเต็มบวก ได้แก่ 1 , 2 , 3 , 4 , 5 ,…
2. จำนวนเต็มลบ ได้แก่ …,-5 , -4 , -3 , -2 , -1
3. ศูนย์ ได้แก่ 0
จำนวนเต็มบวก
“จำนวนเต็มบวก” หรือเรียกอีกอย่างว่า “จำนวนนับ” ก็คือ จำนวนเต็มที่มีค่ามากกว่า 0 ขึ้นไป
ได้แก่ 1, 2, 3, 4, 5,… นับไปเรื่อยๆ ไม่มีที่สิ้นสุด และบอกไม่ได้ด้วยว่าจำนวนนับตัวสุดท้ายคืออะไร
จำนวนเต็มลบ
“จำนวนเต็มลบ” หรือ “เลขติดลบ” เป็นจำนวนเต็มที่มีค่าน้อยกว่าศูนย์ หรือจำนวนที่เป็นตัวเลขด้านซ้ายมือของศูนย์บนเส้นจำนวนนั่นเอง
จำนวนเต็มศูนย์
“จำนวนเต็มศูนย์” ก็คือ 0 นั่นเอง น้องๆต้องจำไว้ว่า
0 ไม่ใช่จำนวนนับ เพราะเมื่อเรานับจำนวนอะไรก็ตามเราไม่ได้เริ่มนับจาก 0 และเราไม่นิยมพูดว่า เรามีปากกา 0 ด้าม
ศูนย์อาจจะมีความหมายว่า “ไม่มี” เช่น ไม่มีดินสอ ไม่มีคน เป็นต้น
หรือศูนย์ไม่ได้แทนความไม่มีก็ได้ อธิบายได้ง่ายๆจากอุณหภูมิ อุณหภูมิที่ 0 องศาเซลเซียส ไม่ได้แปลว่าไม่มีอุณหภูมิ หรือไม่ได้แปลว่าไม่ร้อนไม่หนาว เพราะเราเกิดความรู้สึกในขณะที่อุณหภูมิ 0 องศาเซลเซียนได้
จำนวนธรรมชาติ
เมื่อเรียนเรื่องจำนวนเต็ม ทุกคนอาจจะได้ยินคำว่า “จำนวนธรรมชาติ” จำนวนธรรมชาติในทางคณิตศาสตร์ จะหมายถึง “จำนวนเต็มบวก” หรือ “จำนวนนับ” ได้แก่ 1, 2, 3, 4,… ส่วนทางตรรกศาสตร์และเซต
จะหมายถึง “จำนวนเต็มไม่เป็นลบ” ได้แก่ 0, 1, 2, 3, 4,…
หากดูจากเส้นจำนวนเราจะเห็นได้ว่าตัวเลขที่อยู่ทางขวามือจะมีจำนวนมากกว่าตัวเลขที่อยู่ทางซ้ายมือ
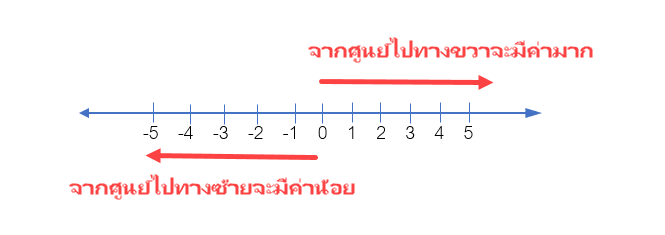
ถ้าดูจากเส้นจำนวนข้างบนทำให้เรารู้ว่าจำนวนเต็มบวก 4 มากกว่าจำนวนเต็มบวก 3
และ จำนวนเต็มบวก 3,4 มากกว่า -4 เป็นต้น
เส้นจำนวน
“เส้นจำนวน” (Number Line) เป็นเส้นตรงที่ถูกลากขึ้นมาเส้นหนึ่ง แล้วให้จุดหนึ่งบนเส้นนั้นแทนด้วยศูนย์ โดยกำหนดให้จุดที่ห่างออกไปทางซ้ายมือของศูนย์เป็นตัวแทนของจำนวนเต็มลบ
โดยแต่ละจุดห่างออกไปช่องละหนึ่งหน่วยเท่าๆกัน และจำนวนเต็มลบที่ถัดจากศูนย์จะเริ่มจาก -1, -2, -3
ในทางกลับกัน จุดทางด้านขวามือของศูนย์ที่ห่างออกไปเป็นช่องยาวหนึ่งหน่วยเท่าๆกัน จะเป็นตัวแทนของจำนวนเต็มบวก โดยเริ่มจาก 1, 2, 3,…
และต้องจำไว้ว่าบนเส้นจำนวนใดๆ จำนวนที่อยู่ทางขวาจะมากกว่าจำนวนที่อยู่ทางซ้ายเสมอ
ชนิดของจำนวนเต็ม มี 3 ชนิด คือ
1. จำนวนเต็มบวก หรือ จำนวนนับ หรือ จำนวนธรรมชาติ ได้แก่ 1, 2, 3, 4, 5,….
2. จำนวนเต็มศูนย์ ได้แก่ 0
3. จำนวนเต็มลบ ได้แก่ -1, -2, -3, -4, -5,……
จำนวนเต็ม จึงแบ่งได้เป็น จำนวนเต็มบวก จำนวนเต็มศูนย์ จำนวนเต็มลบ ได้แก่ …, – 5, – 4, -3, -2, -1, 0 , 1 , 2 , 3 , 4 , 5 ,….. ซึ่งสามารถแสดงบนเส้นจำนวนได้ดังนี้
จำนวนบนเส้นจำนวน จำนวนที่อยู่ซ้ายมือจะมีค่าน้อยกว่าจำนวนที่อยู่ทางขวามือ ดังจะได้ว่า ….< -5 < – 4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5…..
ค่าสัมบูรณ์
ค่าสมบูรณ์คือระยะทางจาก 0 ถึง a บนเส้นจำนวน ใช้สัญลักษณ์ | | แทน ค่าสัมบูรณ์ของจำนวนเต็ม a คือระยะทางจาก 0 ถึง a บนเส้นจำนวน | a | อ่านว่าค่าสัมบูรณ์ของ a
จากรูปจะเห็นได้ว่า | 4 | = 4 , | -4 | = 4 , | 0 | = 0
จำนวนเต็ม a ใดๆ | a | = | – a |
เรียก a ว่าจำนวนตรงข้ามของ -a และเรียก -a จำนวนตรงข้ามของ a
เราจะใช้สัญลักษณ์ที่ใช้แทนค่าสัมบูรณ์ คือ | | เช่น
| -1 | คือ ค่าสัมบูรณ์ของ -1 คือ 1
| 3 | คือ ค่าสัมบูรณ์ของ 3 คือ 3
3 มีระยะห่างจาก 0 เท่ากับ 3 หน่วย นั้นคือ ค่าสัมบูรณ์ของ 3 เท่ากับ 3
-3 มีระยะห่างจาก 0 เท่ากับ 3 หน่วย นั้นคือ ค่าสัมบูรณ์ของ -3 เท่ากับ 3
สมบัติบางประการของจำนวนเต็มบวก
1. สมบัติการสลับที่สำหรับการบวก สำหรับจำนวนเต็มบวก a และ b ใดๆ
จะได้ว่า a + b = b + a
2. สมบัติการสลับที่สำหรับการคูณ สำหรับจำนวนเต็มบวก a และ b ใดๆ
จะได้ว่า a • b = b • a
3. สมบัติการเปลี่ยนกลุ่มสำหรับการบวก สำหรับจำนวนเต็มบวก a , b และ c ใดๆ
จะได้ว่า (a + b) + c = a + (b + c)
4. สมบัติการเปลี่ยนกลุ่มสำหรับการคูณ สำหรับจำนวนเต็มบวก a , b และ c ใดๆ
จะได้ว่า (a • b) • c = a • (b • c)
5. สมบัติการแจกแจง สำหรับจำนวนเต็มบวก a , b และ c ใดๆ
จะได้ว่า a • (b + c) = (a • b) + (a • c)
6. สมบัติของหนึ่ง สำหรับจำนวนเต็มบวก a ใดๆ
จะได้ว่า 1 x a = a = a x 1

7. สมบัติของศูนย์สำหรับจำนวนเต็มบวก a ใดๆ
จะได้ว่า a + 0 = a = 0 + a
a x 0 = 0 = 0 x a
 แต่
แต่  จะไม่มีความหมาย
จะไม่มีความหมาย
การบวก – ลบจำนวนเต็ม
1. ผลบวกระหว่างจำนวนเต็มบวก 2 จำนวน หรือ จำนวนเต็มลบ 2 จำนวน จะมีค่าเท่ากับค่าบวกหรือค่าลบของผลบวกค่าสัมบูรณ์ตามลำดับ
2. ผลบวกระหว่างจำนวนเต็มบวกกับจำนวนเต็มลบ คือ ผลต่างระหว่างค่าสัมบูรณ์ทั้งสองโดยใช้ค่าสัมบูรณ์มากกว่าเป็นตัวตั้ง แล้วใส่เครื่องหมายตามตัวมากกว่า
ตัวอย่างเช่น :
5 + 4 = 9
5 + (–4) = 1
(–5) + 4 = –1
(–5) + (–4) = –9
5 – 4 = 5 + (–4) = 1
5 – (–4) = 5 + 4 = 9
(–5) – 4 = (–5) + (–4) = –9
(–5) – (–4) = (–5) + 4 = –1
การคูณจำนวนเต็ม
สรุป การคูณระหว่างจำนวนเต็มสองจำนวน อาศัยเรื่องผลคูณของค่าสัมบูรณ์ของจำนวนทั้งสอง โดยมีเครื่องหมาย ดังนี้
(+) x (+) = +
(+) x (–) = –
(–) x (+) = –
(–) x (–) = +
การบวก – ลบ – คูณ – หารจำนวนเต็ม
มีหลักดังนี้
1. ถ้ามีวงเล็บให้คิดในเครื่องหมายวงเล็บก่อนเสมอ โดยเริ่มจากวงเล็บเล็ก วงเล็บปีกกา วงเล็บใหญ่
2. ให้ดำเนินการบวก ลบ คูณ หาร ดังที่เรียนมาแล้วข้างต้น
ตัวอย่างเช่น
[{(–3) + 11 – (–8)} % {(–6) + 3 + 11}] x (–2)
= [{(–3) + 11 + (8)} % {(–6) + 3 + 11}] x (–2)
= [16 % 8] x (–2)
= 2 x (–2)
= –4
การเปรียบเทียบจำนวนเต็ม
เมื่อเรานำจำนวนเต็มสองจำนวนมาเปรียบเทียบกัน ผลลัพธ์ที่ได้อยู่ในสามรูปแบบนี้
เพียงอย่างใดอย่างหนึ่งเท่านั้น ได้แก่
จำนวนหนึ่งมากกว่าจำนวนหนึ่ง
จำนวนหนึ่งน้อยกว่าอีกจำนวนหนึ่ง หรือ
จำนวนทั้งสองเท่ากัน
ซึ่งจากหลักการข้างต้น น้องๆ สามารถแทนค่าได้ดังนี้
ถ้า a, b, c เป็นจำนวนธรรมชาติใดๆ แล้ว
a – b = c แล้ว a > b
a – b = -c แล้ว b > a หรือ a < b
a – b = 0 แล้ว a =0 และ b = 0






