คณิตศาสตร์ ม.5 เนื้อหา ลำดับและอนุกรมแบบสรุปย่อ
ลำดับ หมายถึง ฟังก์ชันที่มีโดเมนเป็นเซตของจำนวนเต็มบวกที่เรียงจากน้อยไปมากโดยเริ่มตั้งแต่ 1 ซึ่งลำดับนั้น เป็นจำนวนหรือพจน์ที่เขียนเรียงกันภายใต้กฏเกณฑ์อย่างใดอย่างหนึ่งเป็นลำดับทั่ว ๆ ไป โดยแบ่งออกเป็น 2 ชนิด ได้แก่
- ลำดับจำกัด คือ ลำดับซึ่งมีจำนวนพจน์จำกัด โดยฟังก์ชันจะเป็นลำดับที่มีโดเมนเป็น { 1, 2, 3, …, n }
- ลำดับอนันต์ คือ ลำดับซึ่งมีจำนวนพจน์ไม่จำกัด โดยฟังก์ชันเป็นลำดับที่มีโดเมนเป็น { 1, 2, 3, … }
ลำดับ คือ กลุ่มของตัวเลขที่มีความสัมพันธ์กัน ซึ่งแบ่งออกเป็น 2 รูปแบบใหญ่ ๆ คือ
ลำดับเลขคณิต คือ ลำดับที่มีผลต่างที่ได้จากการนำพจน์ที่ n+1 ลบด้วยพจน์ที่ n แล้วมีค่าคงที่เสมอ
และเรียกผลต่างที่มีค่าคงที่ว่า ผลต่างร่วม ( Common difference )
ถ้า a1, a2, a3, …, an, an+1 , … เป็นลำดับเลขคณิต แล้ว
จะได้ a2 – a1 = a3 – a2 = … = an+1 – an เท่ากับ ค่าคงที่
เรียกค่าคงที่นี้ว่า “ ผลต่างร่วม ” (Common difference) เขียนแทนด้วย “ d ”
จากบทนิยาม d = an+1 – an
หรือ an+1 = an + d
ตัวอย่าง ลำดับเลขคณิต
1. ลำดับ 1, 3, 5, …, 99 เป็นลำดับเลขคณิต มีผลต่างร่วม ( d ) เท่ากับ 2
2. ลำดับ 6, 3, 0, …, -27 เป็นลำดับเลขคณิต มีผลต่างร่วม ( d ) เท่ากับ -3
3. ลำดับ 5, 5, 5, …, 5 เป็นลำดับเลขคณิต มีผลต่างร่วม ( d ) เท่ากับ 0
4. ลำดับ 0, 0, 0, …, 0 เป็นลำดับเลขคณิต มีผลต่างร่วม ( d ) เท่ากับ 0
จากตัวอย่างข้างต้น จะพบว่า d เป็นจำนวนจริงใด ๆ และ ถ้า d = 0 จะได้ว่าทุกพจน์ของลำดับมีค่าเท่ากัน
และเรียกลำดับนี้ว่า “ลำดับคงตัว” เช่น ข้อ 3 และข้อ 4
การหาพจน์ต่าง ๆ ของลำดับเลขคณิต
กำหนดลำดับเลขคณิต a1 , a2 , a3 , … ให้ a1 เป็นพจน์แรกของลำดับ
และ d เป็นผลต่างร่วม จะเขียนพจน์อื่นๆ ของลำดับเลขคณิตในรูปของ a1 และ d ดังนี้
a1 = a1
a2 = a1 + d
a3 = a1 + 2d
a4 = a1 + 3d
.
.
.
an = a1 + ( n – 1 )d
สรุป พจน์ทั่วไปหรือพจน์ที่ n ของลำดับเลขคณิต คือ
an = a1 + ( n – 1 )d
มื่อ an คือ พจน์ที่ n ของลำดับเลขคณิ
a1 คือ พจน์ที่ 1 ของลำดับเลขคณิต
n คือ ตำแหน่งของพจน์ที่ n
d คือ ผลต่างร่วม (พจน์ที่ n+1 ลบด้วย พจน์ที่ n)
ลำดับเรขาคณิต
บทนิยาม ลำดับเรขาคณิต คือ ลำดับที่มีอัตราส่วนของพจน์ที่ n+1 ต่อพจน์ที่ n เป็นค่าคงที่
ทุกค่าของจำนวนนับ n และเรียกค่าคงที่นี้ว่า “ อัตราส่วนร่วม ”
ถ้า a1, a2, a3, …, an, an+1 เป็นลำดับเรขาคณิต แล้ว จะได้

เท่ากับค่าคงที่ เรียกค่าคงที่นี้ว่า “ อัตราส่วนร่วม ” (Common ratio) เขียนแทนด้วย r
พิจารณา ลำดับ 1, 2, 4, 8, …
- ลำดับเรขาคณิต คือ ลำดับที่มีอัตราส่วนของพจน์ที่ n+1 กับพจน์ที่ n โดยมีค่าคงที่เป็นอัตราส่วนร่วม (r)
ตัวอย่าง
3, 6, 12, 24 …. มี r = 2
2, -4, 8, -16 … มี r = -2
ลำดับหลายชั้น เป็นลำดับเลขอนุกรม มีค่าความแตกต่างระหว่างตัวเลขมีลักษณะเป็นเลขอนุกรมด้วย
ลำดับเว้นระยะ เป็นลำดับเลขอนุกรม ซึ่งประกอบด้วยอนุกรมมากกว่า 1 ซ้อนกันอยู่ภายในโจทย์เดียวกัน
ลำดับแบบมีค่าแตกต่างเป็นชุด เป็นลำดับอนุกรมที่เกิดจากค่าความแตกต่างที่เป็นชุด คือหลายตัวประกอบขึ้นมาและใช้ค่าแตกต่างที่เป็นชุดดังกล่าวในการพิจารณาเลขอนุกรมลำดับถัดไป
ลำดับยกกำลัง เป็นลำดับเลขอนุกรม ซึ่งเกิดจากการยกกำลังของตัวเลขต่าง ๆ หรืออาจเกิดจากค่าความแตกต่างที่อาจเป็นเลขยกกำลัง
อนุกรม คือ ผลจากการบวกสมาชิกทุกตัวของลำดับไม่จำกัดเข้าด้วยกัน โดยที่
- ถ้า a1, a2, a3, …, an เป็น ลำดับจำกัด ที่มี n พจน์ เราจะเรียกการเขียนแสดงผลบวกของพจน์ทุกพจน์ของลำดับในรูป a1 + a2 + a3 + … + an ว่า อนุกรมจำกัด
- และ ถ้า a1, a2, a3, …, an, … เป็น ลำดับอนันต์ จะเรียกการเขียนแสดงผลบวกในรูป a1 + a2 + a3 + … + an + … ว่า อนุกรมอนันต์
จากอนุกรม a1 + a2 + a3 + … + an + … โดยทั่วไปจะเรียก
- a1 ว่าพจน์ที่ 1 ของอนุกรม
- a2 ว่าพจน์ที่ 2 ของอนุกรม
- a3 ว่าพจน์ที่ 3 ของอนุกรม
- an ว่าพจน์ที่ n ของอนุกรม
อนุกรมเลขคณิต คือ ผลบวกของลําดับเลขคณิต อธิบายได้ว่า
เมื่อ a1, a1 + d, a1 + 2d, …, a1 + (n – 1)d เป็นลำดับเลขคณิต
จะได้ a1 + (a1 + d) + (a1 + 2d) + … + (a1 + (n – 1)d) เป็นอนุกรมเลขคณิต
ซึ่งมี a 1 เป็นพจน์แรกของอนุกรม และ d เป็นผลต่างร่วมของอนุกรมเลขคณิต ซึ่งจากบทนิยามจะได้ว่า
ถ้า a1, a2, a3, …, an เป็น ลำดับเลขคณิต ที่มี n พจน์ เราจะเรียกการเขียนแสดงผลบวกของพจน์ทุกพจน์ของลำดับ a1 + a2 + a3 + … + an ว่า อนุกรมเลขคณิต และผลต่างร่วม ( d ) ของลำดับเลขคณิต เป็นผลต่างร่วมของอนุกรมเลขคณิตด้วย
ตัวอย่างของอนุกรมเรขาคณิต
1. 2 + 4 + 8 + 16 + … เป็น อนุกรมเรขาคณิต
เพราะ 2, 4, 8, 16, … เป็น ลำดับเรขาคณิต
และมีอัตราส่วนร่วมเท่ากับ 2
2. 81 + 27 + 9 + 3 + … เป็น อนุกรมเรขาคณิต
เพราะ 81, 27, 9, 3, … เป็น ลำดับเรขาคณิต
และมีอัตราส่วนร่วมเท่ากับ
3. 3 + 3 + 3 + 3 + … เป็น อนุกรมเรขาคณิต
เพราะ 3, 3, 3, 3, … เป็น ลำดับเรขาคณิต
และมีอัตราส่วนร่วมเท่ากับ 1
การหาผลบวก n พจน์แรกของอนุกรมเรขาคณิต
ให้ Sn แทนผลบวก n พจน์แรกของอนุกรมเรขาคณิต
ซึ่งมี a1 เป็นพจน์แรก และ r เป็นอัตราส่วนร่วม
Sn = a1 + a1r + a1r2 + … + a1r n-2+ a1r n-1 — (1)
สมการ (1) คูณ r จะได้
rSn = a1r + a1r2+ a1r3 + … + a1r n-2+ a1r n-1 + a1r n — (2)
สมการ (1) – (2) จะได้
Sn – rSn = a1-a1rn
(1 – r)Sn = a1(1-rn)

ผลบวก n พจน์แรกของอนุกรมเรขาคณิต
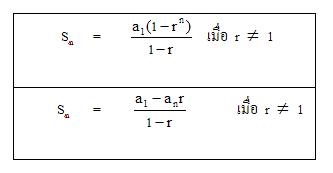
เมื่อ Sn แทนผลบวก n พจน์แรกของอนุกรมเรขาคณิต
a1 แทนพจน์ที่ 1
an แทนพจน์ที่ n
r แทนอัตราส่วนร่วม พจน์ที่ n+1 หารด้วยพจน์ที่ n
ขอบคุณข้อมูล https://www.chulatutor.com/ และ https://jejeelomchoy.wordpress.com/






