คณิตศาสตร์ ออนไลน์-สรุป เมตริกซ์และดีเทอร์มิแนนท์ (Matrix and Determinant)

ระบบสมการเชิงเส้น และเมทริกซ  เมตริกซ์และดีเทอร์มิแนนท์ (Matrix and Determinant)

สรุปเนื้อหา

          1. สัญลักษณ์ของเมตริกซ์
ถ้า A เป็นเมตริกซ์ที่มี m แถว และ n หลัก เรียกว่า A เป็นเมตริกซ์ที่มีมิติ m x n

เมื่อ 1 ≥ i ≥ m และ 1 ≥ i ≥ n

2. การเท่ากันของเมตริกซ์

เมื่อ 1) m = p และ n = q
2) a_ij= b _ij สำหรับทุกๆ ij
3. การบวกเมตริกซ์

1 คุณสมบัติปิดสำหรับการบวก
2 คุณสมบัติเปลี่ยนกลุ่มได้สำหรับการบวก
3 คุณสมบัติสลับที่การบวก
4 เอกลักษณ์การบวก
5 อินเวอร์สการบวก
4. การคูณเมตริกซ์ด้วยสเกลาร์

คุณสมบัติการคูณเมตริกซ์ด้วยสเกลาร์
ให้ A, B เป็น m ? n เมตริกซ์ c และ d เป็นสเกลาร์
1. (cd)A = c(dA) = d (cA)
2. c(A+B) = cA + cB
3. (c + d)A = cA + dA
4. (I)A = A และ (-1) A = -A
5. การคูณเมตริกซ์ด้วยเมตริกซ์
1. คุณสมบัติการเปลี่ยนกลุ่มได้
2. คุณสมบัติการกระจาย
3. การมีเอกลักษณ์
4. การมีอินเวอร์ส

ข้อควรระวัง
1. คุณสมบัติการสลับที่สำหรับการคูณใช้ไม่ได้
2. เมตริกซ์ใดๆ ไม่จำเป็นต้องมีอินเวอร์สำหรับการคูณ
 6. ทรานสโพสเมตริกซ์ (Transposematrix)

คุณสมบัติที่เกี่ยวกับทรานสโพสเมตริกซ์
ถ้า A, B เป็นเมตริกซ์ที่บวกและคูณกันได้ โดยมี k เป็นจำนวนจริง
1. (A¹) ¹ = A
2. (A+B)¹= A¹+B¹
3. (kA¹) = kA¹
4. (AB)¹=B¹A¹
7. เมตริกซ์ซิงกูลาร์และนอนซิงกูลาร์ (Singular Matrix)

คุณสมบัติของเมตริกซ์นอนซิงกูลาร์
1. ถ้า A, B เป็นนอนซิงกูลาร์เมตริกซ์ และมีมิติเท่ากันแล้ว AB เป็นนอนซิงกูลาร์ เมตริกและ (AB)^-1=B^-1A^-1
2. ถ้า A เป็นนอนซิงกูลาร์เมตริกซ์แล้วA¹ เป็นนอนซิงกูลาร์เมตริกซ์และ(A^-1) ^-1 = A
3. ถ้า A, B และ C เป็นเมตริกซ์ที่มีมิติเท่ากัน โดย A เป็นนอนซิงกูลาร์เมตริกซ์จะพบว่า
ถ้า AB = AC แล้ว B = C หรือ ถ้า BA = CA แล้ว B = C
4.A =  เป็นนอนซิงกูลาร์เมตริกซ์ ก็ต่อเมื่อ ad-ab ≠ 0
5.ถ้า A เป็นนอนซิงกูลาร์เมตริกซ์ และ k เป็นสเกลาร์แล้ว kA เป็นนอนซิงกูลาร์เมตริกซ์ และ
6. ถ้า A° เป็นนอนซิงกูลาร์เมตริกซ์แล้ว = (A^-1) ^-1= (A^-1) ^-1

8. ดีเทอร์มิแนนท์ (Determinant)

ไมเนอร์และโคแฟคเตอร์ (Minor and Cofactor)

→ ไมเนอร์ของ a_ij คือ ดีเทอร์มิแนนท์ของเมตริกซ์ A ที่ได้จากตัดแถวที่ i และหลักที่ j ออกจากเมตริกซ์ A
→ โคแฟคเตอร์ของ a_ij คือ ผลคูณของ(-1)^i+j กับไมเนอร์ a_ij ซึ่งเขียนแทนด้วย A_ij หรือ C_ij
ตัวอย่าง

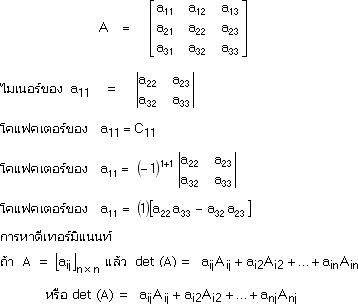
สมบัติของดีเทอร์มิแนนท์
1. ถ้า A เป็น m x n เมตริกซ์ที่มีสมาชิกในแถวใดแถวหนึ่งหรือหลักใดหลักหนึ่ง มีสมาชิกเป็น 0 ทั้งแถว
หรือทั้งหลักแล้ว det(A) = 0
2. ถ้า A เป็น m x n เมตริกซ์ ที่มีสมาชิกในสองแถวใดๆ หรือสองแถวหลักใดๆ เท่ากันแล้ว det (A) = 0
3. ถ้า A เป็น m x m เมตริกซ์ และ B เป็นเมตริกซ์ที่เกิดจากการสลับที่ของสมาชิกในแถวคู่ใดคู่หนึ่ง
หรือในหลักคู่ใดคู่หนึ่งแล้ว det(B) = -det (A)
4. ถ้า A เป็น m x m เมตริกซ์ และ B เป็นเมตริกซ์ที่เกิดจากการนำตัวคงที่ k ไปคูณสมาชิกในแถวใดแถวหนึ่ง
หรือหลักใดหลักหนึ่งของ A แล้ว det (B) = k det (A)
5. ถ้า A เป็น m x m เมตริกซ์ และ B เป็นเมตริกซ์ที่เกิดจากการนำตัวลงที่ไปคูณสมาชิกในแถวใดแถวหนึ่ง
หรือหลักใดหลักหนึ่งแล้วนำไปบวกกับแถวอื่นหรือหลักอื่น det (B) = det (A)
6. det(l_m)=l และ
7. ถ้า A เป็นเมตริกซ์สามเหลี่ยมแล้ว det (A) คือผลคูณของสมาชิกในเส้นทแยงมุมหลัก
8. det A= det A¹,det A · det A^-1=1
9. ถ้า A เป็น m x m เมตริกซ์และ k เป็นค่าคงที่แล้ว det (kA) = k^m det(A)
10. ถ้า A, B เป็น m x m เมตริกซ์แล้ว det (AB) = det (A) det (B)
9. แอดจอยต์เมตริกซ์ (Adjoint Matrix)

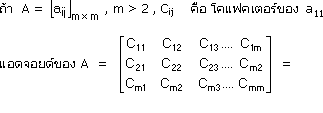
10. การหาอินเวอร์สการคูณของเมตริกซ์
          
det(adj A) = det(adj A)^n-1 เมื่อ A เป็นเมตริกซ์ n x n
11. การแก้สมการเชิงเส้นโดยใช้เมตริกซ์และดีเทอร์มิแนนท์
11.1 การแก้สมการโดยใช้ดีเทอร์มิแนนท์ มีหลักคือ
1. เขียนสมการให้อยู่ในรูปแบบปกติคือ ตัวเลขอยู่ทางขวามือ
2. หาค่า , D_x , D_y , D_z
โดยที่ D หมายถึง ดีเทอร์มินแนนท์ของเมตริกซ์สัมประสิทธิ์
หมายถึง D ที่แทนสัมประสิทธิ์ของ x ด้วยค่าคงตัว
หมายถึง D ที่แทนสัมประสิทธิ์ของ y ด้วยค่าคงตัว
หมายถึง D ที่แทนสัมประสิทธิ์ของ z ด้วยค่าคงตัว

11.2 การแก้สมการโดยใช้อินแวอร์สการคูณของเมตริกซ์
จากสมการ ax + by = m และ cx + dy = n

หรือเขียนเป็น AX = B จะได้ว่า X = A^-1B
เมื่อ X คือเมตริกซ์ของตัวแปร และ A เป็นเมตริกซ์สัมประสิทธิ์ที่มีอินเวอร์ส
11.3 การแก้สมการโดยใช้ปฏิบัติการในแถว
หลักการหา มีดังนี้
1. สร้างเมตริกซ์ของสัมประสิทธิ์และค่าคงที่
2. ใช้วิธีการใดๆ ใน 3 วิธีต่อไปนี้ เพื่อทำให้ส่วนซ้ายมือของเมตริกซ์ที่สร้างจากข้อ 1 เป็นเมตริกซ์เอกลักษณ์
โดยวิธีการอย่างหนึ่งคือ
1. สลับแถว
2. คูณแถวที่ i ด้วย k เมื่อ k ≠ 0
3. นำผลคูณจาก 2 ไปบวกในแถวที่ j