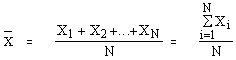คณิตศาสตร์ o-net ม.6 ปีการศึกษา 2565 

หมายถึง การหารผลรวมของข้อมูลทั้งหมดด้วยจำนวนข้อมูลทั้งหมด     การหาค่าเฉลี่ยเลขคณิตสามารถหาได้ 2 วิธี

1. ค่าเฉลียเลขคณิตของข้อมูลที่ไม่ได้แจกแจงความถี่  สามารถคำนวณได้จากสูตร

          x 1 , x 2 , x 3 , …, x N     คือ ผลบวกของข้อมูลทุกค่า

          n    คือ จำนวนข้อมูลทั้งหมด

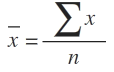
ค่าเฉลี่ยเลขคณิต หรือที่เราเรียกกันย่อๆ ว่าค่าเฉลี่ย เขียนแทนด้วยสัญลักษณ์ (x¯) เป็นค่ากลางทางสถิติค่าหนึ่ง ที่เจอบ่อยและใช้กันเยอะมาก

วิธีการหาค่าเฉลี่ยเลขคณิตของข้อมูลแบบไม่แจกแจงความถี่สามารถทำได้ดังนี้

ตัวอย่าง 1 )  หาค่าเฉลี่ยจากข้อมูลชุดนี้ 1,2,2,5,7,11,15,9

วิธีทำ

ตอบ 6.5

การวัดการกระจายของข้อมูล
การวัดการกระจายของข้อมูล  หมายถึงการคำนวณว่าข้อมูลชุดใดชุดหนึ่งกระจายออกจากกัน  หรืออยู่ห่างกันมากน้อยเพียงใด  ถ้าคะแนนของข้อมูลในชุดใดอยู่ห่างกันน้อยหรือมีขนาดใกล้เคียงกัน  เรียกว่าข้อมูลชุดนั้นมีการกระจายน้อย  แต่ถ้าคะแนนของข้อมูลในชุดใดอยู่ห่างกันมาก  เรียกว่าข้อมูลชุดนั้นมีการกระจายมาก
การอธิบายลักษณะของข้อมูลโดยวิธีการวัดแนวโน้มเข้าสู่ส่วนกลางเป็นการอธิบาย ลักษณะของข้อมูลเพียงลักษณะเดียว  ส่วนลักษณะอื่นๆไม่สามารถแสดงได้ด้วยการวัดแนวโน้มเข้าสู่ส่วนกลาง  ตัวอย่าง  เช่น
ข้อมูลชุดที่ 1 :        5    11    18    25    41
ข้อมูลชุดที่ 2 :      14    20    21    22    23

มัชฌิมเลขคณิตของข้อมูลชุดที่ 1    =  (5 + 11 + 18 + 25 + 41) / 5
=  100 / 5
=  20
มัชฌิมเลขคณิตของข้อมูลชุดที่ 2    =  (14 + 20 + 21 + 22 + 23) / 5
=  100 / 5
=  20

จะเห็นว่าค่ามัชฌิมเลขคณิตของข้อมูลทั้งสองชุดมีค่าเท่ากัน  โดยที่ลักษณะของข้อมูลทั้งสองชุดต่างกัน  ข้อมูลชุดที่ 1 ประกอบด้วยคะแนนที่มีค่าสูงสุดและต่ำสุดแตกต่างกันมาก  ส่วนข้อมูลชุดที่ 2  ประกอบด้วยคะแนนที่มีค่าใกล้เคียงกัน  ซึ่งการใช้มัชฌิมเลขคณิตเป็นตัวแทนของข้อมูลทั้งสองชุด  ทำให้ผู้ที่ไม่ทราบข้อมูลทั้งสองชุดมีความเข้าใจผิดว่าข้อมูลทั้งสองชุดนั้น มีลักษณะเหมือนกัน  ดังนั้นจึงจำเป็นต้องมีการวัดการกระจายของข้อมูลด้วย  เพื่อทำให้ทราบลักษณะของข้อมูลชัดเจนยิ่งขึ้น
การวัดการกระจายของข้อมูล  สามารถทำได้  ดังนี้  คือ

• พิสัย (Range)
• ส่วนเบี่ยงเบนควอร์ไทล์ (Quartile Deviation)
• ส่วนเบี่ยงเบนเฉลี่ย  (Mean Deviation or Average Deviation)
• ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation)

5.2  พิสัย (Range)
พิสัย  หมายถึงความแตกต่างระหว่างคะแนนสูงสุดกับคะแนนต่ำสุดในข้อมูลชุดหนึ่งๆ  พิสัยใช้ในการวัดการกระจายของข้อมูลได้ไม่ละเอียดนัก  นิยมใช้กรณีเมื่อต้องการความรวดเร็วเท่านั้น  ข้อเสียของพิสัยของข้อมูลแต่ละชุด  คือมีการใช้เฉพาะคะแนนสูงสุดและคะแนนต่ำสุดเท่านั้น  บางครั้งทำให้เกิดการเข้าใจถึงลักษณะของข้อมูลผิดไปได้  ตัวอย่าง  เช่น

ข้อมูลชุดที่ 1 :        5   30   32   39   42   50
ข้อมูลชุดที่ 2 :      42   44   46   48   49   51

พิสัยของข้อมูลชุดที่ 1        =  50 – 5               =  45
พิสัยของข้อมูลชุดที่ 2        =  51 – 42            =   9

จะเห็นว่าพิสัยของข้อมูลทั้งสองชุดต่างกันมาก  ทั้งๆที่ข้อมูลทั้งสองชุดนั้นมีลักษณะคล้ายคลึงกันมาก

5.3  ส่วนเบี่ยงเบนควอร์ไทล์ (Quartile Deviation)
ส่วนเบี่ยงเบนควอร์ไทล์  หมายถึงครึ่งหนึ่งของระยะจากควอร์ไทล์ที่ 3  (Q3)  ถึงควอร์ไทล์ที่ 1  (Q1)  ของคะแนนในชุดนั้นๆ  ส่วนเบี่ยงเบนควอร์ไทล์ป็นการวัดการกระจายของข้อมูล  กรณีที่ใช้การวัดแนวโน้มเข้าสู่ส่วนกลางด้วยมัธยฐาน

โดยใช้สูตร           Q.D =
เมื่อ                         Q.D =    ส่วนเบี่ยงเบนควอร์ไทล์
Q3    =    ควอร์ไทล์ที่ 3
Q1    =    ควอร์ไทล์ที่ 1

                ตัวอย่าง                 จากข้อมูลที่ให้จงหาค่าส่วนเบี่ยงเบนควอร์ไทล์

คะแนน	ความถี่	ความถี่สะสม
5 – 9 10 – 14 15 – 19 20 – 24 25 – 29 30 – 34 35 – 39	3 4 10 15 14 10 4	3 7 17 32 46 56 60
	N = 60

จากหัวข้อก่อนเรื่องค่ากลางของข้อมูล มัธยฐานเป็นค่าที่สามารถหาได้จากการพิจารณาตำแหน่งที่อยู่ตรงกลางของชุดข้อมูลเมื่อเรียงลำดับแล้ว ซึ่งค่ามัธยฐานบอกให้เราทราบว่ามีข้อมูลที่น้อยกว่าหรือมากกว่าค่ากลางนี้เป็นปริมาณเท่าๆ กัน
นอกจากการหาตำแหน่งข้อมูลที่อยู่ตรงกลางแล้ว เรายังสามารถหาตำแหน่งข้อมูลตัวใดก็ได้ ตรงไหนก็ได้ในชุดข้อมูลนั้นโดยเรียงลำดับข้อมูลจากน้อยไปมากก่อน จากนั้นแบ่งข้อมูลออกเป็นกลุ่มๆ และเทียบตำแหน่งข้อมูลตัวที่ต้องการกับข้อมูลที่เหลือ ซึ่งเราเรียกว่า การหาตำแหน่งสัมพัทธ์ของข้อมูล
ตำแหน่งสัมพัทธ์ของข้อมูลที่นิยมใช้มีอยู่ 3 แบบ ได้แก่
1) ควอร์ไทล์ (Quartile) – ภายหลังจากเรียงข้อมูลแบบน้อยไปมากแล้ว จะแบ่งข้อมูลออกเป็น 4 กลุ่มเท่าๆ กัน ซึ่งจะเกิดจุดแบ่ง 3 จุด ดูรูปประกอบนะคะ

เรียกจุดแบ่งเหล่านี้ว่า ควอร์ไทล์ที่ 1 (Q₁), ควอร์ไทล์ที่ 2 (Q₂) และ ควอร์ไทล์ที่ 3 (Q₃) ตามลำดับ
– ที่ Q₁ บอกให้เราทราบว่า มีจำนวนข้อมูลที่มีค่าน้อยกว่าจุดนี้อยู่ประมาณ 1/4 (25%) และมีจำนวนข้อมูลที่มีค่ามากกว่าจุดนี้อยู่ประมาณ 3/4 (75%)
– ที่ Q₂ เราทราบได้ว่า มีจำนวนข้อมูลที่มีค่าน้อยกว่าจุดนี้อยู่ประมาณครึ่งหนึ่งของข้อมูลทั้งหมด (50%) และมีจำนวนข้อมูลที่มีค่ามากกว่าจุดนี้อยู่ประมาณครึ่งหนึ่งเช่นกัน
– ที่ Q₃ ทำให้เราทราบว่า มีจำนวนข้อมูลที่มีค่าน้อยกว่าจุดนี้อยู่ประมาณ 3/4 (75%) และมีจำนวนข้อมูลที่มีค่ามากกว่าจุดนี้อยู่ประมาณ 1/4 (25%)

ตัวอย่างการหาค่าตำแหน่งสัมพัทธ์ สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่

ข้อมูลรายได้ต่อเดือนของชาวบ้าน 10 คนในหมู่บ้านแห่งหนึ่ง เป็นดังนี้
5500   3100   4700   6300   3100   2800   4500   6100   5000    5200
ให้หาค่ามัธยฐาน ควอร์ไทล์ที่ 3 และเปอร์เซนไทล์ที่ 60 ของข้อมูลชุดนี้

Solⁿ ก่อนอื่นต้องเรียงลำดับข้อมูลจากน้อยไปมากก่อน จะได้
2800  3100   3100   4500   4700   5000   5200   5500   6100   6300
1) มัธยฐาน
ตำแหน่งของมัธยฐาน = (10+1)/2 = 5.5 ซึ่งเป็นตำแหน่งตรงกลางระหว่างตำแหน่งที่ 5 กับ 6 ดังนั้นต้องคิดเฉลี่ยแบ่งครึ่งเอา
ค่ามัธยฐาน = (4700+5000)/2 = 4850 บาท
2) ควอร์ไทล์ที่ 3

ตำแหน่ง Q₃ =

= 8.25 ซึ่งอยู่ระหว่างตำแหน่งที่ 8 และ 9 (5500 และ 6100)
Q₃ = 5500+0.25(6100-5500) = 5650 บาท
3) เปอร์เซนไทล์ที่ 60
ตำแหน่ง P₆₀ =

= 6.6 ซึ่งอยู่ระหว่างตำแหน่งที่ 6 และ 7 (5000 และ 5200)

P₆₀ = 5000+0.6(5200-5000) = 5120 บาท