กฎของสเตฟาน–โบลทซ์มานน์ (Stefan-Boltzmann’s Law)
ความเข้มของพลังงาน (Energy Flux) แปรผันตามค่ายกกำลังสี่ของอุณหภูมิ มีหน่วยเป็น จูล / ตารางเมตร วินาที หรือ วัตต์ / ตารางเมตร
| F = δT4 |
F = ความเข้มของพลังงาน มีหน่วยเป็นวัตต์ / ตารางเมตร (W m-2)
δ = 5.67 x 10-8 วัตต์ / ตารางเมตร K4 (W m-2 K-4)
T = อุณหภูมิของวัตถุ มีหน่วยเป็นเคลวิน (K)
ถ้าเราทราบว่า ความยาวคลื่นเข้มสุดที่ดาวแผ่รังสีออกมา เราก็จะทราบอุณหภูมิพื้นผิวของดาว (ดังตัวอย่างที่ 1) และเมื่อเราทราบอุณหภูมิพื้นผิวของดาว เราก็จะทราบว่า พลังงานที่ดาวแผ่ออกมานั้นมีความเข้มเท่าไร (ดังตัวอย่างที่ 3)
| ตัวอย่างที่ 3: พื้นผิวของดวงอาทิตย์มีอุณหภูมิเฉลี่ย 5,800 K มีความเข้มของพลังงานเท่าไร F = δT4 = (5.67 x 10-8 วัตต์ / ตารางเมตร K4) (5800 K)4 = (5.67 x 10-8 วัตต์ / ตารางเมตร) (1.13 x 1015) = 64,164,532 วัตต์ / ตารางเมตร |
ความสัมพันธ์ระหว่างพลังงานและระยะทาง
ในการแผ่รังสี คลื่นแม่เหล็กไฟฟ้าแผ่ออกจากจุดกำเนิดทุกทิศทุกทาง เปรียบเสมือนทรงกลมที่มีจุดกำเนิดเป็นจุดศูนย์กลาง โดยเมื่อพลังงานแพร่ออกไป ความเข้มของพลังงานจะลดลงไปเท่ากับ หน่วยของระยะทางยกกำลังสอง ดังที่แสดงในภาพที่ 2
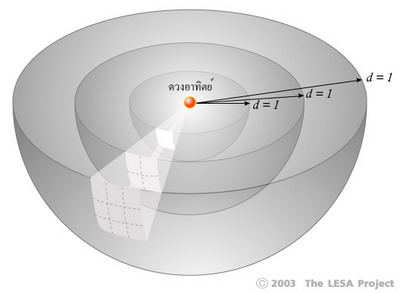
ภาพที่ 2 กฏของสเตฟาน–โบลทซ์มานน์
กฎระยะทางผกผันกำลังสอง
| F1 / F2 = (D2 / D1)2 |
F1 = ความเข้มของพลังงาน ณ ระยะทางที่ 1
F2 = ความเข้มของพลังงาน ณ ระยะทางที่ 2
D1 = ระยะทางจากจุดกำเนิดถึงระยะทางที่ 1
D2 = ระยะทางจากจุดกำเนิด ถึงระยะทางที่ 2
ตัวอย่างที่ 4 แสดงให้เห็นว่า ดวงอาทิตย์มีรัศมี 694 ล้านเมตร พื้นผิวของดวงอาทิตย์แผ่รังสีด้วยความเข้ม 64 ล้านวัตต์ / ตารางเมตร แสงอาทิตย์เดินทางมายังโลกเป็นระยะทาง 149.6 ล้านกิโลเมตร ซึ่งมีระยะห่างมากกว่ารัศมีของดาวอาทิตย์ 216 เท่า ทำให้แสงอาทิตย์มีความเข้มน้อยลง (216)2 เท่า ดังนั้น แสงอาทิตย์ตกกระทบบรรยากาศชั้นบนของโลกด้วยความเข้มเพียง 1,370 วัตต์/ตารางเมตร
| ตัวอย่างที่ 4: พลังงานที่พื้นผิวของดวงอาทิตย์มีความเข้ม 64 ล้านวัตต์ / ตารางเมตร อยากทราบว่า พลังงานจากดวงอาทิตย์ที่ตกกระทบบรรยากาศชั้นบนของโลก จะมีความเข้มเท่าไร F1 = ความเข้มของพลังงาน ณ บรรยากาศโลกชั้นบน F2 = ความเข้มของพลังงาน ณ ผิวดวงอาทิตย์ = 64,000,000 วัตต์/ตารางเมตร D1 = รัศมีของวงโคจรโลกรอบดวงอาทิตย์ = 149.6 x 109 เมตร D2 = รัศมีของดวงอาทิตย์ = 694,000,000 เมตร F1 = F2 (D2/D1)2 F1 = (64 x 106 วัตต์/ตารางเมตร) (694 x 106 เมตร / 149.6 x 109 เมตร)2 = 1,370 วัตต์/ตารางเมตร |
สรุปกฎการแผ่รังสี
| 1. | คลื่นแม่เหล็กไฟฟ้าเคลื่อนที่ในอวกาศด้วยความเร็ว 300,000 กิโลเมตร/วินาที | |
| 2. | คลื่นสั้นมีความถี่สูง คลื่นยาวมีความถี่ต่ำ | |
| 3. | วัตถุทุกชนิดที่มีอุณภูมิสูงกว่า 0 K (-273°C) ล้วนมีพลังงานภายในตัว และมีการแผ่รังสีคลื่นแม่เหล็กไฟฟ้า | |
| 4. | วัตถุที่มีอุณหภูมิสูง ย่อมมีการแผ่พลังงาน (อัตราการไหลของพลังงาน) มากกว่าวัตถุที่มีอุณหภูมิต่ำ | |
| 5. | พลังงานของโฟตอนแปรผันโดยตรงกับความถี่ (E = hλ) | |
| 6. | พลังงานของโฟตอนแปรผกผันกับความยาวคลื่น (E = hc /λ) | |
| 7. | วัตถุที่มีอุณหภูมิสูงแผ่รังสีคลื่นสั้น วัตถุที่มีอุณหภูมิต่ำแผ่รังสีคลื่นยาว (λmax = 0.0029 / T) |
|
| 8. | ความเข้มของพลังงานแปรผกผันกับหน่วยของระยะทางยกกำลังสอง (F1/F2 = (D2/D1)2) | |
การคำนวณหาพลังงานจากดวงอาทิตย์
| 1. | Spectrum จากดวงอาทิตย์ มีความยาวคลื่นที่มีพลังงานสูงสุดλmax = 500 นาโนเมตร กฎของเวน T = 0.0029 / λmax ทำให้ทราบค่าอุณหภูมิพื้นผิว = 5,800 K ……..(ตัวอย่างที่ 1) | |
| 2. | กฎสเตฟาน-โบลทซ์มานน์ F = δ T4 ทำให้ทราบค่าความเข้มของพลังงานที่พื้นผิว = 64 ล้านวัตต์/ตารางเมตร ……..(ตัวอย่างที่ 3) |
|
| 3. | กฎระยะทางผกผันกำลังสอง F1 / F2 = (D2 / D1)2 ทำให้ทราบค่าความเข้มของพลังงานที่ตกกระทบบรรยากาศของโลก = 1,370 ล้านวัตต์ / ตารางเมตร ……..(ตัวอย่างที่ 4) |