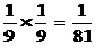ความน่าจะเป็นและกฎที่สำคัญบางประการของความน่าจะเป็น
การทดลองสุ่ม ( Random experiment) คือการทดลองที่ไม่สามารถทำนายผลลัพธ์ได้อย่างถูกต้อง
ตัวอย่าง การโยนเหรียญขึ้นไปในอากาศ ถือว่าเป็นการทดลองสุ่ม เพราะยังไม่ทราบว่าเหรียญจะหงายหัวหรือก้อย
การทอดลูกเต๋า 1 ลูก ถือว่าเป็นการทดลองสุ่ม เพราะยังไม่ทราบว่าลูกเต๋าจะขึ้นแต้ม 1, 2, 3, 4, 5 หรือ6
แซมเปิลสเปซ ( Sample space) คือเซตของผลลัพธ์ที่อาจเป็นไปได้ทั้งหมดของการทดลองสุ่ม
ตัวอย่าง เช่น ในการโยนเหรียญ 2 อัน 1 ครั้ง ถ้ามีผลลัพธ์ที่เราสนใจคือ การขึ้นหัวหรือก้อย
จะได้แซมเปิลสเปซ คือ {(H, H), (H, T), (T, H), (T, T)} เมื่อ (H, T) หมายถึงเหรียญอันที่1 ขึ้นหัว และเหรียญอันที่ 2 ขึ้นก้อย
ในการโยนเหรียญ 2 อัน 1 ครั้ง ถ้ามีผลลัพธ์ที่เราสนใจคือ จำนวนก้อยที่ขึ้น จะได้แซมเปิลสเปซ คือ {0, 1, 2}
เมื่อ 0 หมายถึงไม่ขึ้นก้อยทั้ง 2 อัน (นั่นคือขึ้นหัวทั้งสองอัน)
1 หมายถึงขึ้นก้อยเพียง 1 อัน (ขึ้นหัว 1 อัน)
2 หมายถึงขึ้นก้อยทั้ง 2 อัน
เหตุการณ์ ( Event) คือสับเซตของแซมเปิลสเปซ
ความน่าจะเป็น ของเหตุการณ์
คือ โอกาสที่จะเกิดเหตุการณ์ที่สนใจเท่ากับเท่าใด
หลักการหาความน่าจะเป็น
ให้ S เป็นแซมเปิลสเปซ ซึ่งแต่ละผลลัพธ์ใน S มีโอกาสเกิดขึ้นเท่าๆกัน E เป็นสับเซตของ S
ให้ P (E) เป็นสัญลักษณ์แทน ความน่าจะเป็นของเหตุการณ์ E เราสามารถหา P(E) ได้ดังนี้
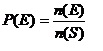
ตัวอย่าง ความน่าจะเป็นที่ A เรียงเป็นตัวแรก จากการเรียงตัวอักษร 2 ตัวจากอักษร 3 ตัว คือ A, B และ C
S = {AB, BA, AC, CA, BC, CB}
E = { AB , AC }
![]()
![]()
กฎสำคัญบางประการของความน่าจะเป็น
ให้ A เป็นเหตุการณ์ใดๆ และ S เป็นแซมเปิลสเปซ สมบัติความน่าจะเป็นของ A ดังนี้
1. 0 P (A) 1
2. ถ้า A = { } แล้ว P (A) = 0 นั่นคือ P ( { } ) = 0
3. ถ้า A = S แล้ว P (A) = 1 นั่นคือ P(S) = 1
สมบัติของความน่าจะเป็นของเหตุการณ์ 2 เหตุการณ์
ให้ A และ B เป็นเหตุการณ์ 2 เหตุการณ์ ใน S แซมเปิลสเปซ
1. P (A U B) = P (A) + P (B) – P (A ∩B)
2. P (A U B) = P (A) + P (B) เมื่อ A ∩B = { }
3. P (A) = 1 – P (A’)
4. P (A-B) = P (A) – P (A∩B)
ตัวอย่าง กำหนดให้ P (A) = 0.6 P (B’) = 0.4 และ P (A – B) = 0.2 จงหา P (A ‘∩B’)
จาก P (B’) = 0.4
จะได้ว่า P (B) = 1 – P (B’) = 1 – 0.4 = 0.6
จาก P (A) = 0.6 และ P (A – B) = 0.2
เนื่องจาก P (A) = P (A – B) + P (A ∩B)
(ถ้านักเรียนไม่เข้าใจให้เขียนแผนภาพทางด้านเซตดู)
0.6 = 0.2 + P (A ∩ B)
P (A ∩B) = 0.4
เนื่องจาก P (A’ ∩ B’) = P (A U B)’
= 1 – P (A U B)
จากสมบัติความน่าจะเป็น P (A’ ∩B’) = 1 – [P (A) + P (B) – P (A ∩B)]
= 1 – [0.6 + 0.6 – 0.4] = 1 – 0.8 = 0.2
ความน่าจะเป็นแบบเงื่อนไข
บางครั้งเราทราบว่าเหตุการณ์หนึ่งเกิดขึ้น เราต้องการหาความน่าจะเป็นที่อีกเหตุการณ์หนึ่งเกิดขึ้น เรียกความน่าจะเป็นแบบนี้ว่า ความน่าจะเป็นแบบเงื่อนไข
ให้ A และ B เป็นเหตุการณ์ โดยที่ P (B) > 0 เขียน P (A/B) แทนความน่าจะเป็นของ A เมื่อกำหนดว่าเหตุการณ์ B เกิดขึ้นแล้ว
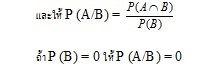
ความน่าจะเป็นของเหตุการณ์ที่เป็นอิสระต่อกัน
พิจารณาในการโยนเหรียญ 1 อัน 2 ครั้ง จะเห็นว่าการที่การโยนเหรียญครั้งหนึ่งขึ้นหัวหรือก้อย ไม่มีผลต่อการขึ้นหัวหรือก้อยในการโยนครั้งที่สอง
เรากล่าวว่าการโยนทั้งสองครั้งเป็นอิสระต่อกัน
นิยาม เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (A ∩B) = P (A) P (B)
ทฤษฎีบท เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (A/B) = P (A)
เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (B/A) = P (B)
ตัวอย่าง โยนลูกเต๋า 2 ลูก 2 ครั้ง จงหาความจะเป็นที่ผลรวมของแต้มแต่ละครั้งเท่ากับ 5
ให้ A แทนเหตุการณ์ที่ผลรวมของแต้มในการโยนครั้งที่ 1 เป็น 5
B แทนเหตุการณ์ที่ผลรวมของแต้มในการโยนครั้งที่ 2 เป็น 5
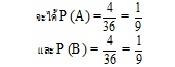
เนื่องจากการโยนลูกเต๋าแต่ละครั้งเป็นอิสระต่อกัน
ดังนั้นความน่าจะเป็นที่ผลรวมของแต้มแต่ละครั้งเป็น 5 เท่ากับ
P (A∩ B) = P (A) P (B)