ความสัมพันธ์
คู่อันดับ และผลคูณคาร์ทีเซียน
| • คู่อันดับ |
|
คู่อันดับประกอบด้วยสมาชิก 2 ตัว เขียนแทนคู่อันดับในรูป (a,b) โดยที่ a เป็นสมาชิกตัวหน้าและ b เป็นสมาชิกตัวหลัง อันดับของสมาชิกถือว่าสำคัญ กล่าวคือการสลับที่กันระหว่างสมาชิกทั้งสองอาจทำให้ความหมายของคู่อันดับเปลี่ยนไปได้
|
| |
สมบัติของคู่อันดับ |
| |
1. (a,b) = (b,a) ก็ต่อเมื่อ a = b |
| |
2. ถ้า (a,b) = (c,d) แล้วจะได้ a = c และ b = d |
| |
3. ถ้า (a,b) ≠ (c,d) แล้วจะได้ a ≠ c หรือ b ≠ d |
| |
|
|
|
|
|
| • ผลคูณคาร์ทีเซียน |
|
ผลคูณคาร์ทีเซียนของเซต A และเซต B คือเซตของคู่อันดับ (a,b) ทั้งหมดซึ่ง a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B และเขียนแทนด้วย A× B
|
| |
นั่นคือ A× B = { (a,b) | a ∈ A และ b ∈ B } |
| |
สมบัติของผลคูณคาร์ทีเซียน |
| |
กำหนด A, B และ C เป็นเซตใดๆ แล้ว |
| |
1.
|
A× B ไม่จำเป็นต้องเท่ากับ B × A |
| |
A× B = B × A ก็ต่อเมื่อ A = B หรือ A = Ø หรือ B = Ø |
| |
A× B ≠ B × A ก็ต่อเมื่อ A ≠ B ≠ Ø |
| |
2. |
A × Ø = Ø × A = Ø |
| |
3. |
A × ( B ∪ C )
|
= (A× B) ∪(A × C) |
| |
|
(A ∪ B) × C |
= (A× C) ∪(B × C) |
| |
4. |
A × ( B ∩ C ) |
= (A× B) ∩ (A × C) |
|
|
| |
|
(A ∩ B) × C |
= (A× B) ∩ (B × C) |
|
|
| |
5. |
A × ( B – C ) |
= (A× B) – (A × C) |
|
|
| |
|
(A – B) × C ) |
= (A× C) – (B × C) |
กราฟของความสัมพันธ์
| ในระบบแกนมุมฉาก เราสามารถจับคู่หนึ่งต่อหนึ่ง ระหว่างคู่อันดับของจำนวนจริง (x, y) กับพิกัดของจุดบนระนาบ โดยให้ x เป็นพิกัดแรก และ y เป็นพิกัดหลัง จากหลักการดังกล่าวทำให้เราสามารถเขียนกราฟของความสัมพันธ์ได้ดังนี้ |
| บทนิยาม |
| ให้ R เป็นเซตของจำนวนจริง และ r เป็นสับเซตของ R× R กราฟของความสัมพันธ์ r คือ เซตของจุดบนระนาบ โดยที่แต่ละจุดแทนสมาชิกของความสัมพันธ์ R |
|
| |
|
| ตัวอย่างที่ 1 |
จงเขียนกราฟของความสัมพันธ์ |
| |
r = { (x,y) ∈ A × A | x + y = 5} เมื่อกำหนดให้ |
| |
A = {1, 2, 3, 4} |
| วิธีทำ |
r = {(1, 4), (2, 3), (3, 2), (4, 1)} |
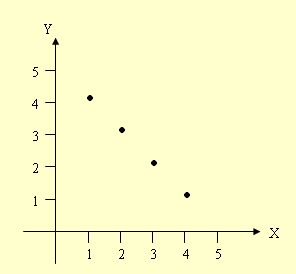
| ตัวอย่างที่ 2 |
จงเขียนกราฟของความสัมพันธ์ |
| |
r = { (x,y) ∈ R × R | y = x – 1} |
| วิธีทำ |
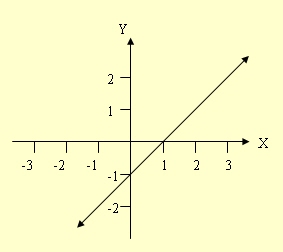
| ตัวอย่างที่ 3 |
จงเขียนกราฟของความสัมพันธ์ |
| วิธีทำ |
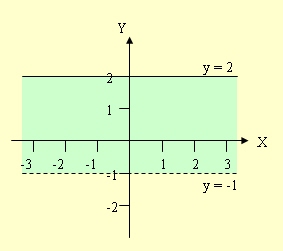
r = { (x,y) ∈ R × R | -1 < y ≤ 2 } |
| ตัวอย่างที่ 4 |
จงเขียนกราฟของความสัมพันธ์ |
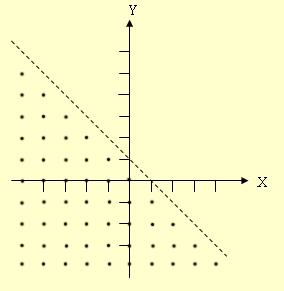
| วิธีทำ |
r = { (x,y) ∈ I × I | x + y < 1 } |
อินเวอร์สของความสัมพันธ์
|
อินเวอร์สของความสัมพันธ์ r คือ ความสัมพันธ์ซึ่งเกิดจากการสลับตำแหน่งของสมาชิกตัวหน้า และสมาชิกตัวหลัง ในแต่ละคู่อันดับที่เป็นสมาชิกของ r เขียนแทนด้วย r-1
|
| การสลับตำแหน่งของสมาชิกตัวหน้า และสมาชิกตัวหลัง ทำได้ 2 วิธี ดังนี้ |
| |
วิธีที่ 1 |
สลับที่ x และ y ในคู่อันดับ (x, y) แต่มีเงื่อนไขเหมือนเดิม |
| |
|
ตัวอย่างเช่น |
r = {(x, y) ∈ R × R | y = 3x – 1} |
| |
|
|
r-1 = {(y, x) ∈ R × R | y = 3x – 1} |
| |
วิธีที่ 2 |
สลับที่ x และ y ในคู่อันดับ (x, y) โดยแทนที่ x ด้วย y และแทนที่ y ด้วย x แต่ คู่อันดับ (x, y ) เหมือนเดิม |
| |
|
ตัวอย่างเช่น |
r = {(x, y) ∈ R × R | y = 3x – 1} |
| |
|
|
r-1 = {(x, y) ∈ R × R | x = 3y – 1} |
| |
|
|
| r-1 = {(x, y) ∈ R × R | |
|
} |
|
|
สมบัติเกี่ยวกับอินเวอร์สของความสัมพันธ์
|
| |
ถ้า r เป็นความสัมพันธ์จากเซต A ไปเซต B
|
| |
1. r-1เป็นความสัมพันธ์จากเซต B ไปเซต A |
| |
2. D r = R r-1 และ R r = D r-1 |
| |
|
กราฟของอินเวอร์สของความสัมพันธ์
|
| |
เราสามารถวาดกราฟของอินเวอร์สของความสัมพันธ์ได้ 2 วิธีด้วยกัน ดังนี้
|
| |
วิธีที่ 1 |
| |
1. หาอินเวอร์สของความสัมพันธ์ r-1 |
| |
2.วาดกราฟของอินเวอร์สของความสัมพันธ์ โดยใช้เงื่อนไขที่ระบุใน r-1 |
| |
|
ตัวอย่างเช่น |
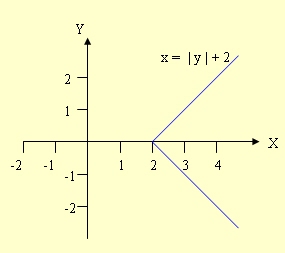
r = {(x, y) ∈ R × R | y = | x | + 2}
|
| |
|
|
r-1 = {(x, y) ∈ R × R | x = | y | + 2} |
| |
|
| |
วิธีที่ 2 |
| |
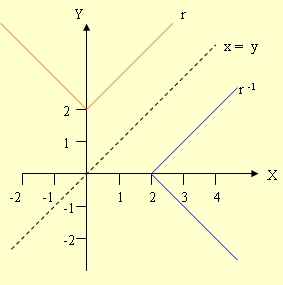
1.วาดกราฟของความสัมพันธ์ r |
| |
2.กราฟของอินเวอร์สของความสัมพันธ์ คือภาพสะท้อนของกราฟของความสัมพันธ์ r รอบแกน x = y |
ฟังก์ชัน
ความหมายของฟังก์ชัน
| ฟังก์ชัน คือ ความสัมพันธ์ซึ่งในสองคู่อันดับใดๆ ของความสัมพันธ์นั้น ถ้าสมาชิกตัวหน้าเหมือนกันแล้ว สมาชิกตัวหลังต้องไม่ต่างกัน |
| นั่นคือ |
| ถ้า (x1,y1) ∈ r และ (x1,y2) ∈ r แล้ว y1= y2 |
|
|
| หลักในการพิจารณาว่าความสัมพันธ์เป็นฟังก์ชันหรือไม่ |
| 1. ถ้าความสัมพันธ์นั้นอยู่ในรูปแจกแจงสมาชิก ให้ดูว่าสมาชิกตัวหน้าของคู่อันดับซ้ำกันหรือไม่ ถ้าสมาชิกตัวหน้าของคู่อันดับซ้ำกัน แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน |
2. ถ้าความสัมพันธ์นั้นอยู่ในรูปของการกำหนดเงื่อนไขสมาชิก
r = {(x,y) ∈ A× B | P(x,y) } ให้แทนค่าแต่ละสมาชิกของ x ลงในเงื่อนไข P(x,y) เพื่อหาค่า y ถ้ามี x ตัวใดที่ให้ค่า y มากกว่า 1 ค่า แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน |
3. พิจารณาจากกราฟของความสัมพันธ์ โดยการลากเส้นตรงขนานกับแกน y ถ้าเส้นตรงดังกล่าวตัดกราฟของความสัมพันธ์มากกว่า 1 จุด แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน
|
ลักษณะของฟังก์ชัน
| • ฟังก์ชันจาก A ไป B |
| f เป็นฟังก์ชันจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนคือเซต A และเรนจ์เป็นสับเซตของเซต B เขียนแทนด้วย f : A → B |
| • ฟังก์ชันจาก A ไปทั่วถึง B |
| f เป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็นเซต A และเรนจ์เป็นของเซต B เขียนแทนด้วย f : A → B |
| • ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B |
f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันจาก A ไป B ซึ่งถ้า y ∈ R f
แล้วมี x ∈ Df เพียงตัวเดียวเท่านั้นที่ทำให้ (x,y) ∈ f เขียนแทนด้วย f : A ไป B
หรืออาจกล่าวอย่างง่ายๆได้ว่า f เป็นฟังก์ชันหนึ่งต่อหนึ่ง ก็ต่อเมื่อสำหรับ x1และ x2 ในโดเมน ถ้า
f( x1) = f( x2) แล้ว x1 = x2 |
| • ฟังก์ชันเพิ่ม ฟังก์ชันลด |
| |
ให้ f เป็นฟังก์ชันจากสับเซตของ R× R และ A ⊂ Df |
| |
♦ f เป็นฟังก์ชันเพิ่มใน A ก็ต่อเมื่อ สำหรับสมาชิก x1 และ x2 ใดๆ ใน A |
| |
|
ถ้า x1 < x2 แล้ว f( x1) < f( x2)
|
|
| |
♦ f เป็นฟังก์ชันลดใน A ก็ต่อเมื่อ สำหรับสมาชิก x1 และ x2 ใดๆ ใน A |
| |
|
ถ้า x1 < x2 แล้ว f( x1) > f( x2)
|
|