ความสัมพันธ์และฟังก์ชัน มีหน่วยย่อย ดังนี้
- คู่อันดับและผลคูณคาร์ทีเซียน
- ความสัมพันธ์
- กราฟของความสัมพันธ์
- การประยุกต์ของกราฟ
- ฟังก์ชัน
- ฟังก์ชันต่างๆ บางชนิด
- แบบต่างๆ ของฟังก์ชัน
- ฟังก์ชันผกผัน
- การบวก การลบ การคูณ การหาร และการคูณด้วยจำนวนจริงของฟังก์ชัน
- ฟังก์ชันประกอบ
| สมบัติของคู่อันดับ | ||||
| 1. (a,b) = (b,a) ก็ต่อเมื่อ a = b | ||||
| 2. ถ้า (a,b) = (c,d) แล้วจะได้ a = c และ b = d | ||||
| 3. ถ้า (a,b) ≠ (c,d) แล้วจะได้ a ≠ c หรือ b ≠ d | ||||
| ผลคูณคาร์ทีเซียนของเซต A และเซต B คือเซตของคู่อันดับ (a,b) ทั้งหมดซึ่ง a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B และเขียนแทนด้วย A× B | |||||
| นั่นคือ A× B = { (a,b) | a ∈ A และ b ∈ B } | |||||
| สมบัติของผลคูณคาร์ทีเซียน | |||||
| กำหนด A, B และ C เป็นเซตใดๆ แล้ว | |||||
| 1. | A× B ไม่จำเป็นต้องเท่ากับ B × A | ||||
| A× B = B × A ก็ต่อเมื่อ A = B หรือ A = Ø หรือ B = Ø | |||||
| A× B ≠ B × A ก็ต่อเมื่อ A ≠ B ≠ Ø | |||||
| 2. | A × Ø = Ø × A = Ø | ||||
| 3. | A × ( B ∪ C )
|
= (A× B) ∪(A × C) | |||
| (A ∪ B) × C | = (A× C) ∪(B × C) | ||||
| 4. | A × ( B ∩ C ) | = (A× B) ∩ (A × C) | |||
| (A ∩ B) × C | = (A× B) ∩ (B × C) | ||||
| 5. | A × ( B – C ) | = (A× B) – (A × C) | |||
| (A – B) × C ) | = (A× C) – (B × C) | ||||
| 6. | ถ้า A ⊂ B แล้ว A × C ⊂ B × C | ||||
| 7. | ถ้า A และ B เป็นเซตจำกัดแล้ว n( A × B ) = n(A) × n(B) | ||||
| 8. | ถ้่า A เป็นเซตอนันต์ และ B เป็นเซตจำกัด ซึ่ง B ≠ Ø แล้ว A × B เป็นเซตอนันต์ | ||||
ความสัมพันธ์เป็นหัวข้อทางคณิตศาสตร์ที่มีบทบาทมากในการวิเคราะห์ความเกี่ยวข้องกันระหว่างสมาชิกในเซตเดียวกับหรือสมาชิกต่างเซตกัน โดยสมาชิกที่สัมพันธ์กันจะถูกเขียนในรูปของคู่อันดับ ถ้าเราให้ S เป็นเซตของนักเรียน และ C เป็นเซตของวิชา ถ้านักเรียนคนที่ s ได้ลงเรียนวิชา c นั้นคือนักเรียน s และวิชา c สัมพันธ์กันในลักษณะของการลงเรียนวิชาเขียนแทนด้วยคู่อัน (s,c) โดยที่คู่อันดับ (s,c) เป็นสมาชิกของผลคูณคาร์ทีเซียน S x C เมื่อเรารวบรวมคู่อัน (s,c) ทั้งหมดเราจะได้เซตที่แสดงถึงความสัมพันธ์ของนักเรียนกับวิชาที่เรียน นอกจากนี้หากนักเรียน s ได้ลงเรียนวิชา c1, c2 และ c4 เราสามารถแทนด้วยคู่อันดับ
( s, { c1, c2, c4 } ) ซึ่งเป็นสมาชิกของผลคูณคาร์ทีเซียน S x P(C) โดยที่ P(C) คือเพาเวอร์เซตของเซต C
ตัวอย่างที่ 1 กำหนดให้ A = { a, b } จงหา A x P(A)
วิธีทำ พิจารณา P(A) = { { }, {a}, {b}, { a, b } } จะได้ว่า
A x P(A) = { (a, { }), (a, {a}), (a, {b}), (a, { a, b }), (b, { }), (b, {a}), (b, {b}), (b, { a, b }) }
ตัวอย่างที่ 2 ถ้า A และ B เป็นเซตที่มีจำนวนสมาชิกเท่ากับ 3 และ 5 ตามลำดับจำนวนความสัมพันธ์ของ A และ B ที่แตกต่างกันมีค่าเท่าใด
วิธีทำ เนื่องจาก n(A) = 3 และ n(B) = 5 จะได้ว่า n( A x B ) = 15 ความสัมพันธ์คือการเลือกหรือรวบรวมผลคูณคาร์ทีเซียนของ A และ B นั้นคือเซตย่อยของ A x B ดังนั้นจำนวนความสัมพันธ์ที่เป็นไปได้ทั้งหมดจะเท่ากับจำนวนเซตย่อยของ A x B เท่ากับ 215
ความหมายของฟังก์ชัน
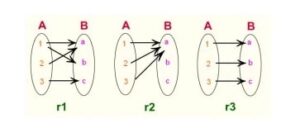
| ฟังก์ชัน คือ ความสัมพันธ์ซึ่งในสองคู่อันดับใดๆ ของความสัมพันธ์นั้น ถ้าสมาชิกตัวหน้าเหมือนกันแล้ว สมาชิกตัวหลังต้องไม่ต่างกัน | |||
|
|||
| หลักในการพิจารณาว่าความสัมพันธ์เป็นฟังก์ชันหรือไม่ | |||
| 1. ถ้าความสัมพันธ์นั้นอยู่ในรูปแจกแจงสมาชิก ให้ดูว่าสมาชิกตัวหน้าของคู่อันดับซ้ำกันหรือไม่ ถ้าสมาชิกตัวหน้าของคู่อันดับซ้ำกัน แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน | |||
| 2. ถ้าความสัมพันธ์นั้นอยู่ในรูปของการกำหนดเงื่อนไขสมาชิก r = {(x,y) ∈ A× B | P(x,y) } ให้แทนค่าแต่ละสมาชิกของ x ลงในเงื่อนไข P(x,y) เพื่อหาค่า y ถ้ามี x ตัวใดที่ให้ค่า yมากกว่า 1 ค่า แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน |
|||
| 3. พิจารณาจากกราฟของความสัมพันธ์ โดยการลากเส้นตรงขนานกับแกน y ถ้าเส้นตรงดังกล่าวตัดกราฟของความสัมพันธ์มากกว่า 1 จุด แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน |
-ขอบคุณข้อมูล https://www.scimath.org/
