ความสัมพันธ์และฟังก์ชัน

คู่อันดับ
คู่อันดับประกอบด้วยสมาชิกสองตัว เขียนแทนคู่อันดับในรูป (a,b) โดยที่ a เป็นสมาชิกตัว
หน้า และ b เป็นสมาชิกตัวหลัง
การสลับที่กันของคู่อันดับระหว่างสมาชิกตัวหน้ากับสมาชิกตัวหลัง (a,b) (b,a) จะท าให้
ความหมายของคู่อันดับเกิดการเปลี่ยนทันที ดังนั้น จึงสามารถสรุปหลักการของคู่อันดับได้ ดังนี้
1. ถ้า (a,b) = (b,a) ก็ต่อเมื่อ a=b
2. ถ้า (a,b) = (c,d) ก็ต่อเมื่อ a=c และ b=d
3. ถ้า (a,b) ≠ (c,d) ก็ต่อเมื่อ a≠ c หรือ b≠ d

ผลคูณคาร์ทีเซียน(Cartesian product)

ให้ A และ B เป็นเซตสองเซตใด ๆ ผลคูณคาร์ทีเซียนของ A และ B

เขียนแทนด้วย A×B (อ่านว่า A ครอส B) เป็นเซตของคู่อันดับทั้งหมดที่เป็นไปได้

โดยที่สมาชิกตัวแรกของคู่อันดับเป็นสมาชิกของ A และสมาชิกตัวหลังของคู่อับดับ

เป็นสมาชิกของ B

นั้นคือ A×B = {(a , b) | a A , b B }

ตัวอย่างที่ 2.1

การหาผลคูณคาร์ทีเซียน

กำหนด A = {1,2,3} , B = {a,b}

1. A×B = { (1,a) , (1,b) , (2,a) , (2,b) , (3,a) , (3,b) }

2. B×A = { (a,1) , (a,2) , (a,3) , (b,1) , (b,2) , (b,3) }

3. A×A = { (1,1) , (1,2) , (1,3) , (2,1) , (2,2) , (2,3) , (3,1) , (3,2) , (3,3) }

4. B×B = { (a,a) , (a,b) , (b,a) , (b,b) }

คุณสมบัติของผลคูณคาร์ทีเซียน

ผลคูณคาร์ทีเซียน
ผลคูณคาร์ทีเซียนของเซต A และเซต B คือเซตของคู่อันดับ (a,b) ทั้งหมดซึ่ง a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B และเขียนแทนด้วย A× B
	นั่นคือ A× B = { (a,b) \| a ∈ A และ b ∈ B }
	สมบัติของผลคูณคาร์ทีเซียน
	กำหนด A, B และ C เป็นเซตใดๆ แล้ว
	1.	A× B ไม่จำเป็นต้องเท่ากับ B × A
		A× B = B × A ก็ต่อเมื่อ A = B หรือ A = Ø หรือ B = Ø
		A× B ≠ B × A ก็ต่อเมื่อ A ≠ B ≠ Ø
	2.	A × Ø = Ø × A = Ø
	3.	A × ( B ∪ C )	= (A× B) ∪(A × C)
		(A ∪ B) × C	= (A× C) ∪(B × C)
	4.	A × ( B ∩ C )	= (A× B) ∩ (A × C)
		(A ∩ B) × C	= (A× B) ∩ (B × C)
	5.	A × ( B – C )	= (A× B) – (A × C)
		(A – B) × C )	= (A× C) – (B × C)

กราฟของความสัมพันธ์

ในระบบแกนมุมฉาก เราสามารถจับคู่หนึ่งต่อหนึ่ง ระหว่างคู่อันดับของจำนวนจริง (x, y) กับพิกัดของจุดบนระนาบ โดยให้ x เป็นพิกัดแรก และ y เป็นพิกัดหลัง จากหลักการดังกล่าวทำให้เราสามารถเขียนกราฟของความสัมพันธ์ได้ดังนี้

บทนิยาม

ให้ R เป็นเซตของจำนวนจริง และ r เป็นสับเซตของ R× R กราฟของความสัมพันธ์ r คือ เซตของจุดบนระนาบ โดยที่แต่ละจุดแทนสมาชิกของความสัมพันธ์ R


ตัวอย่างที่ 1	จงเขียนกราฟของความสัมพันธ์
	r = { (x,y) ∈ A × A \| x + y = 5} เมื่อกำหนดให้
	A = {1, 2, 3, 4}
วิธีทำ	r = {(1, 4), (2, 3), (3, 2), (4, 1)}

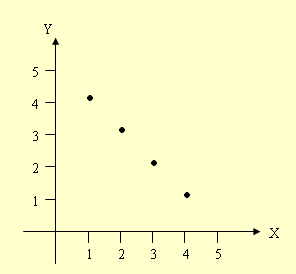
ความสัมพันธ์ของผลรวม

เนื่องจากความสัมพันธ์ จาก A ไป B เป็นเซตย่อยของ AX B
ดังนั้นความสัมพันธ์ 2 ความสัมพันธ์ จาก A ไป B สามารถนำมากระทำกันตามการกระทำบนเซตได้

ตัวอย่างที่ 17 ให้ A = {1,2,3} และ B = {1,2,3,4} R₁และ R₂เป็นความสัมพันธ์ จาก A ไป B
กำหนดโดย R₁= {(1,1),(2,2),(3,3)} และ R₂= {(1,1),(1,2),(1,3),(1,4)} จะได้ว่า

R₁ศ R₂= {(1,1),(1,2),(1,3),(1,4),(2,2),(2,3)}
R₁ว R₂= {(1,1)}
R₁– R₂= {(2,2),(3,3)}
R₂– R₁= {(1,2),(1,3),(1,4)}

นิยาม 6 ให้ R เป็นความสัมพันธ์จากเซต A ไปเซต B
S เป็นความสัมพันธ์จากเซต B ไปเซต C
ส่วนประกอบของ R และ S คือ ความสัมพันธ์ ซึ่งประกอบด้วยคู่อันดับ
(a, c) โดยที่ a ฮ A , c ฮ C โดยที่มี b ฮ B ที่ทำให้ (a,b) ฮ R และ (b,c) ฮ S
เขียนแทน ส่วนประกอบของ R และ S ด้วย SoR

ตัวอย่างที่ 18 ให้ A = {1,2,3} , B = {1,2,3,4} และ C = { 0, 1, 2}
R เป็นความสัมพันธ์จากเซต A ไปเซต B กำหนดโดย R = { (1,1) , (1,4), (2,3), (3,1) , (3,4) }
S เป็นความสัมพันธ์จากเซต B ไปเซต C กำหนดโดย S = { (1,0), (2,0) ,(3,1) ,(3,2), (4,1) }จงหา SoR

วิธีทำ

พิจารณา คู่อันดับ (1,1) ใน R จะเห็นได้ว่าสมาชิกในพิกัดที่ 2 คือ 1 คราวนี้ก็ดูว่า
คู่อันดับใน S ที่มีสมาชิกในพิกัดที่ 1 เป็น 1 มีไหม ให้เอามาทั้งหมด
ซึ่งในที่นี้มีเพียงคู่อันดับเดียวคือ (1,0)
ดังนั้น คู่อันดับ (1,0) จึงอยู่ใน SoR
สำหรับคู่อันดับอื่นนั้นก็พิจารณาในแบบเดียวกันจึงได้ว่า
SoR = { (1,0) ,(1,1) ,(2,1) ,(2,2) ,(3,0) ,(3,1) }