ความสัมพันธ์และฟังก์ชัน

ความสัมพันธ์และฟังก์ชัน

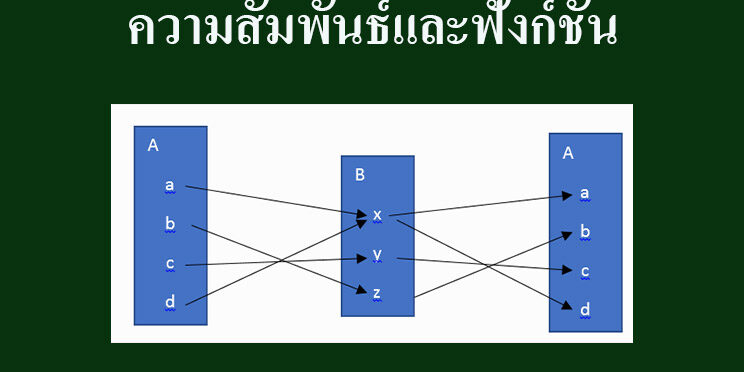
ฟังก์ชัน คือ ความสัมพันธ์ จาก เซต หนึ่ง (โดเมน) ไปยังอีกเซตหนึ่ง (โคโดเมน ไม่ใช่ เรนจ์) โดยที่สมาชิกตัวหน้าไม่ซ้ำกัน ความคิดรวบยอดของฟังก์ชันนี้เป็นพื้นฐานของทุกสาขาของคณิตศาสตร์และวิทยาศาสตร์เชิงปริมาณ

คู่อันดับคู่อันดับประกอบด้วยสมาชิกสองตัว เขียนแทนคู่อันดับในรูป (a,b) โดยที่ a เป็นสมาชิกตัว
หน้า และ b เป็นสมาชิกตัวหลัง
การสลับที่กันของคู่อันดับระหว่างสมาชิกตัวหน้ากับสมาชิกตัวหลัง (a,b) (b,a) จะท าให้
ความหมายของคู่อันดับเกิดการเปลี่ยนทันที ดังนั้น จึงสามารถสรุปหลักการของคู่อันดับได้ ดังนี้
1. ถ้า (a,b) = (b,a) ก็ต่อเมื่อ a=b
2. ถ้า (a,b) = (c,d) ก็ต่อเมื่อ a=c และ b=d
3. ถ้า (a,b) (c,d) ก็ต่อเมื่อ a c หรือ b d
ผลค ูณคาร์ทีเชียน
ผลคูณคาร์ทีเชียนของเซต A และ B คือ เซตของคู่อันดับ (a,b) ที่มีสมาชิกตัวหน้าเป็น
เซตของ A และสมาชิกตัวหลังเป็นเซตของ B กล่าวคือ
AxB = {(a,b) | a∊A, b∊B}

สมบัติของผลค ูณคาร์ทีเชียล
ก าหนด A, B และ C เป็นเซตใดๆ
1. AxB BxA
2. Ax⏀=⏀xA=⏀
3. AxB=BxA ก็ต่อเมื่อ A=B หรือ A=⏀ หรือ B=⏀
4. Ax(B∪C)=(AxB)∪(AxC)
5. Ax(B∩C)=(AxB)∩(AxC)
6. Ax(B-C)=(AxB)-(AxC)
7. ถ้า A และ B เป็นเซตจ ากัดแล้ว n(AxB) = n(A) x n(B)
8. ถ้า A เป็นเซตอนันต์ และ B เป็นเซตจ ากัด ซึ่ง B 0 แล้ว AxB และ BxA เป็น เซตอนันต์

ความสัมพันธ์
– r เป็นความสัมพันธ์จากเซต A ไปเซต B ก็ต่อเมื่อ r⊂AxB
– r เป็นความสัมพันธ์ในเซต A ก็ต่อเมื่อ r⊂AxA
– จำนวนความสัมพันธ์จากเซต A ไปเซต B เท่ากับ 2
n(AxB)
– เป็นความสัมพันธ์จากเซต A ไปเซต B เนื่องจาก ⏀⊂AxB

ถ้าความสัมพันธ์เขียนอยู่ในรูป r={(x,y)∊RxR | y=x² } จะเขียนได้ว่า r={(x,y) | y=x² }
ตัวผกผันของความสัมพันธ์
ตัวผกผันของความสัมพันธ์เขียนแทนด้วย r^-1
จะได้ว่า r^-1 { (y,x) | (x,y) ∊ r}