ความหมายของเซต-คณิตศาสตร์เชิงวิทยาศาสตร์
เซต คืออะไร?
เซต คือ กลุ่มของสิ่งต่างๆ ที่สนใจ โดยเมื่อกล่าวถึงกลุ่มใดจะสามารถบอกได้แน่นอน ว่าสิ่งใดอยู่กลุ่ม สิ่งใดไม่อยู่ในกลุ่ม มักใช้อักษรภาษาอังกฤษตัวใหญ่ในการกล่าวถึงเซต เช่น กลุ่มของประเทศในเอเชีย
- ตัวอย่างเซตเช่น เซตของประเทศในเอเชียตะวันออกเฉียงใต้
- ตัวอย่างของสิ่งที่ไม่ใช่เซต เช่น เซตของคนหน้าตาดี (เพราะไม่สามารถบอกได้แน่ชัดว่าแต่ละคนอยู่หรือไม่อยู่ในกลุ่มนี้)
สมาชิก คือ สิ่งที่อยู่ในเซต โดยใช้สัญลักษณ์ ∈ แทนการเป็นสมาชิกของเซต
ในทางคณิตศาสตร์ เราใช้คำว่าเซตในความหมายของคำว่า กลุ่ม หมู่ เหล่า กอง ฝูง ชุด และเมื่อกล่างถึงเซตของสิ่งใด ๆ จะทราบได้ทันทีว่าในเซตนั้นมีอะไรบ้าง เราเรียกสิ่งที่อยู่ในเซตว่า สมาชิก
| เซต | สมาชิกของเซตประกอบด้วย |
| เซตของวันในหนึ่งสัปดาห์ | วันอาทิตย์, วันจันทร์, วันอังคาร, วันพุธ, วันพฤหัสบดี, วันศุกร์, วันเสาร์ |
| เซตของจำนวนเต็มบวกที่หารด้วย 5 ลงตัว | 5, 10, 15, 20, 25, 30, 35, … |
| เซตของคำตอบของสมการ X2 – 4 = 0 | 2, -2 |
สัญลักษณ์ที่ใช้แทนเซต ชื่อและสมาชิกของเซต
- สามารถใช้วงกลม, วงรี แทนเซตต่าง ๆ ได้
- ชื่อเซตนิยมใช้ตัวใหญ่ทั้งหมด เช่น A, B, C, …
- สัญลักษณ์
แทนคำว่า “เป็นสมาชิกของ”
แทนคำว่า “ไม่เป็นสมาชิกของ” - ตัวอย่างเช่น ให้ A แทนเซตของตัวอักษรที่เป็นสระในภาษาอังกฤษ ซึ่งสามารถเขียนแจกแจง
สมาชิกทุกตัวของเซต A ด้วย A = { a, e, i, o, u }
เนื่องจาก ตัวอักษร “a” เป็นสมาชิกของเซต A เขียนแทนด้วย a∊A
ตัวอักษร “b” ไม่เป็นสมาชิกของเซต A เขียนแทนด้วย b∉A
และ เซต A มีสมาชิก 5 ตัว เขียนแทนด้วย n(A) = 5
สัญลักษณ์ “∊” ใช้แสดงว่า “เป็นสมาชิกของ”
สัญลักษณ์ “∉” ใช้แสดงว่า “ไม่เป็นสมาชิกของ” และ
n(A) ใช้แสดง “ จ”านวนของสมาชิกของเซต A ”
การเขียนเซต
โดยทั่วไปมีวิธีเขียนเซตได้สองแบบ ดังนี้
1) การเขียนเซตแบบแจกแจงสมาชิก เป็นการเขียนสมาชิกทุกตัวของเซตลงในเครื่องหมายวงเล็บปากกา และคั่นสมาชิก
แต่ละตัวด้วยเครื่องหมายจุลภาค (,) เช่น เซตของจำนวนเต็ม บวกที่น้อยกว่า 5 เขียนแทนด้วย { 1, 2, 3, 4 }
ในกรณีที่เซตมีจำนวนสมาชิกมาก นิยมใช้ (…) เพื่อ
แสดงว่ามีสมาชิกอื่น ๆ ที่เข้าใจตรงกันว่ามีสมาชิกใดบ้างในเซตนั้น เช่น A = { 1, 2, 3, …, 9 }
สัญลักษณ์ … แสดงว่ามี 4, 5, 6, 7 และ 8 เป็นสมาชิกของเซตด้วย
1) กำาหนด A = { x | x เป็นจำนวนเต็มบวก และ 2 ≤ x < 11 }
และ B = { x | x เป็นจำนวนเต็มบวกตั้งแต่ 3 ถึง 11 }
(1) ให้เขียนเซต A และเซต B แบบแจกแจงสมาชิก
(2) ให้ตรวจสอบว่า เซต A และเซต B มีสมาชิกเหมือนกันหรือไม่ เพราะเหตุใด
2) ให้เขียนเซต C แบบบอกเงื่อนไขของสมาชิก เมื่อ C = { 5, 10, 15, 20, 25, … }
วิธีทำ 1) (1) A = { 2, 3, 4, 5, 6, 7, 8, 9, 10 }
B = { 3, 4, 5, 6, 7, 8, 9, 10, 11 }
(2) เนื่องจาก 2∊A แต่ 2∉B
ดังนั้น เซต A และเซต B มีสมาชิกไม่เหมือนกัน
2) C = { x | x เป็นจำนวนเต็มบวกที่เป็นพหุคูณของ 5 } หรือ
C = { x | x = 5n เมื่อ n เป็นจำนวนนับ }
1. เซต เป็นการอธิบายการรวมกันของสิ่งต่างๆ ซึ่งสามารถระบุได้ว่าสิ่งใดอยู่หรือไม่อยู่ในเซต
นั้นอย่างชัดเจน (well-defined) และเรียกสิ่งที่อยู่ในเซตว่า สมาชิก (element)
2. โดยทั่วไปมีวิธีเขียนเซตได้ 2 แบบ คือ
1) การเขียนเซตแบบแจกแจงสมาชิก เช่น A = { 2, 4, 6, 8 }
2) การเขียนเซตแบบบอกเงื่อนไขของสมาชิก เช่น
A = { x | x เป็นจำานวนคู่บวกที่น้อยกว่า 10 }
3. เซตจำกัด เป็นเซตที่มีจำนวนสมาชิกเท่ากับศูนย์ หรือเท่ากับจำานวนเต็มบวกใด ๆ
4. เซตอนันต์ เป็นเซตที่มีจำนวนสมาชิกมากมายนับไม่ถ้วน ซึ่งไม่สามารถบอกจำนวนสมาชิก
ของเซตได้
5. เซต A เท่ากับเซต B หมายถึง สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และสมาชิก
ทุกตัวของเซต B เป็นสมาชิกของเซต A นั่นคือ A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A
6. เซตว่าง เป็นเซตที่ไม่มีสมาชิกอยู่เลย เขียนแทนด้วยสัญลักษณ์ { } หรือ ∅
7. เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบข่ายในการพิจารณาสมาชิกของเซตที่กล่าวถึง
เขียนแทนด้วยสัญลักษณ์ 𝒰
8. การเขียนแผนภาพเวนน์แทนเซตจะช่วยให้เข้าใจความสัมพันธ์ระหว่างเซตต่าง ๆ ได้ง่าย
และชัดเจนมากขึ้น
9. เซต A เป็นสับเซตของเซต B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B
เขียนแทนด้วย A ⊂ B
10. เซต A เป็นสับเซตแท้ของเซต B ก็ต่อเมื่อ A ⊂ B และ A ≠ B
11. ถ้าเซต A มีสมาชิกเท่ากับ n ตัว แล้วจำนวนสับเซตทั้งหมดของ A เท่ากับ 2n
เซต
12. เพาเวอร์เซตของเซต A คือ เซตของสับเซตทั้งหมดของ A เขียนแทนด้วย P(A) และถ้าเซต A
มีสมาชิกเท่ากับ n ตัว แล้วจำนวนสมาชิกของ P(A) เท่ากับ 2n
ตัว นั่นคือ n(P(A)) = 2n
13. ถ้า A และ B เป็นสับเซตของเอกภพสัมพัทธ์แล้ว จะได้ว่า
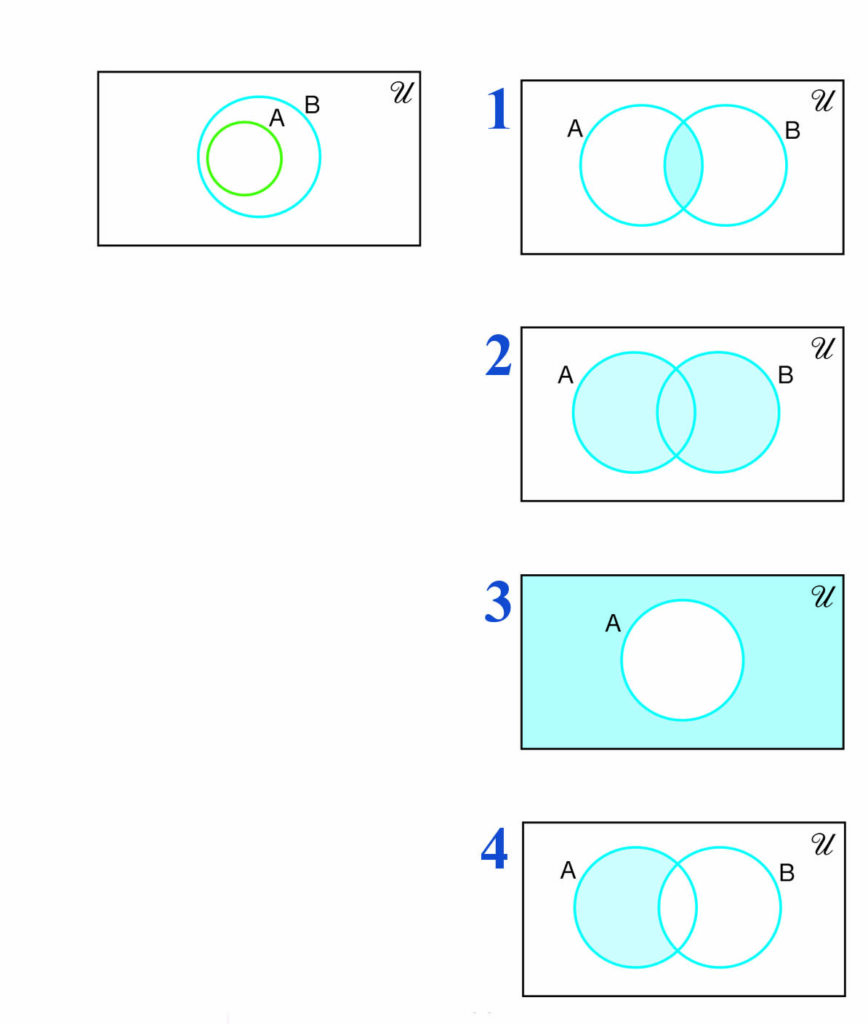
1) อินเตอร์เซกชันของเซต A และเซต B คือ เซตของ
สมาชิกที่ซำกันของเซต A และเซต B เขียนแทนด้วย
A ∩ B นั่นคือ A ∩ B = { x | x∊A และ x∊B }
2) ยูเนียนของเซต A และเซต B คือ เซตของสมาชิกที่
อยู่ในเซต A หรือเซต B เขียนแทนด้วย A ∪ B นั่นคือ
A ∪ B = {x | x∊A หรือ x∊B หรือ x เป็นสมาชิก
ของทั้งสองเซต}
3) คอมพลีเมนต์ของเซต A คือ เซตของทุกสมาชิก
ในเซต 𝒰 แต่ไม่อยู่ในเซต A เขียนแทนด้วย A′ นั่นคือ
A′ = {x | x∊𝒰 และ x∉A}
4) ผลต่างระหว่างเซต A และเซต B หรือคอมพลีเมนต์
ของเซต B เทียบกับเซต A คือ เซตที่มีสมาชิกอยู่ใน
เซต A แต่ไม่อยู่ในเซต B เขียนแทนด้วย A - B นั่นคือ
A - B = {x | x∊A และ x∉B}
14. ถ้า A และ B เป็นเซตจำกัดใด ๆ แล้ว จะได้ว่า n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
15. ถ้า A, B และ C เป็นเซตจำกัดใด ๆ แล้ว จะได้ว่า
(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)
