ความเร่งเนื่องจากแรงโน้มถ่วง ของโลก
ค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก
หลายๆคนที่เคยเรียนวิชาฟิสิกส์ คงจะรู้จักค่า g หรือ ค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก ซึ่งในตอนที่เรียนนั้น จะมีการใช้งานอยู่ 2 ค่า คือ g = 10 m/s2และ g = 9.81 m/s2คำถามต่อมาก็ คือ แล้วค่า g จริงๆแล้วมีค่าเท่าไร และมีที่มาอย่างไร
ในความเป็นจริงแล้ว ค่า g ไม่ใช่ซึ่งค่าคงที่ในทุกๆต่ำแหน่งบนโลก แต่จะมีค่าแปรแปลี่ยนไปตามภูมิประเทศต่างๆ บนโลก
ค่า g นี้สามารถเขียนเป็นสมการความสัมพันธ์ได้ดัง กฎความโน้มถ่วงของนิวตัน (Newton’s Law of Graitation) ได้ดังนี้
g =GM/R2
เมื่อ
g = ค่าความเร่งเนื่องจากแรงโน้มถ่วง
G = ค่าคงตัวโน้มถ่วงสากล (Uniersal graitational constant)= 6.67×10- 11นิวตัน(เมตร)2/(กิโลกรัม)2
M = มวลของโลก = 5.98 x 1024กิโลกรัม
R = รัศมีของโลก = 6.37×106
จากสมการที่ใช้ในการหาค่า g จะพบว่า ค่า g จะแปรผกผันกับค่า R หรือรัศมีระหว่างจุดศูนย์กลางของโลกกับจุดที่คุณต้องการหาค่า g นั่นแสดงว่า ถ้าคุณต้องการค่า g มากที่สุด ก็ต้องหาว่าบริเวณใดที่อยู่ต่ำกว่า ระดับน้ำทะเลมากๆ หรือ มีค่า R น้อยๆ นั่นเอง ในกรณีนี้ผมมีข้อมูลว่า ในประเทศสหรัฐอเมริกามีจุดที่ต่ำที่สุดอยู่ที่ Death alley คือ -282 ft (-85.9536m) สามารถคำนวณหาค่า g ได้ดังนี้
จากสมการ g =GM/R2
แทนค่าต่างๆ ได้
g =((6.673×10- 111)(5.98×1024))/(6.37×106– 85.9536)2
g =9.834565215 m/s2
ลองเปรียบเทียบกับค่า g ที่ได้จากการคำนวณจากค่า R = 6.37×106คือ 9.834299811 m/s2โดยมีค่าที่แตกต่างกันประมาณ 0.000265404 m/s2ซึ่งจะพบว่าค่าที่แตกต่างกันนี้ไม่มีผลมากนักในการคำนวณ หรือจะเรียกได้ว่า ตัดทิ้งได้ ดังนั้นในการใช้งานค่า g จริงๆ แล้ว ควรใช้ที่ค่า g = 9.83 m/s2น่าจะถูกต้องกว่า แต่ก็ขึ้นอยู่กับว่า สิ่งที่เรากำลังคำนวณนั้นต้องการความละเอียดแค่ไหน
ในกรณีของประเทศไทย หากคุณต้องการทราบค่า g ที่สูงที่สุด หรือต้องการทราบค่า g ที่บริเวณที่ คุณอยู่ ก็ต้องทราบว่าที่ๆ คุณอยู่ตอนนี้มีความสูง ของพื้นที่เป็นอย่างไร สูงหรือต่ำกว่าระดับน้ำทะเล เท่าไร ลองคำนวณดูได้เลยครับ
ประวัติการค้นพบค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก
แรกเริ่มเดิมทีนั้น มนุษย์เชื่อว่า “เมื่อปล่อยวัตถุสองชิ้นซึ่งมีมวลต่างกันจากที่สูงเท่ากันพร้อมๆกันภายใต้แรงโน้มถ่วงของโลก วัตถุที่มีมวลมากกว่าจะตกถึงพื้นก่อน” ซึ่งความคิดนี้ถูกนำเสนอไว้โดย”อริสโตเติล” นักปราชญ์ชาวกรีก ซึ่งความคิดนี้ได้รับการยอมรับ และเชื่อถือต่อมาอีกหลายร้อยปีโดยปราศจากการทดลอง ตรวจสอบหรือแม้แต่กาตั้งคำถามถึงความถูกต้อง
กาลิเลโอ กาลิเลอี กับการทดลอง ณ หอเอนเมืองปิซ่า
การศึกษาถึงทฤษฎีความโน้มถ่วงสมัยใหม่ได้ถูกนำเสนอเป็นครั้งแรกโดย กาลิเลโอ กาลิเลอี (Galileo Galilei ค.ศ. 1564 – 1642 ) ในช่วงปลายทศวรรษที่ 16 การทดลองที่มีชื่อเสียงของกาลิเลโอ คือ การทดลองปล่อยวัตถุที่มีมวลต่างกัน 2 ชิ้น จากยอดหอเอนปิซา ในเวลาพร้อมกัน ซึ่งวัตถุดังกล่าว ได้ตกลงมาภายใต้แรงโน้มถ่วงโลก และถึงพื้นเกือบจะพร้อมๆ กัน ซึ่งเป็นการพิสูจน์ว่าความคิดของอริสโตเติลนั้นไม่ถูกต้อง (ในปัจจุบันยังเป็นที่ถกเถียงกันว่ากาลิเลโอได้ทำการทดลองดังกล่าวจริงหรือเป็นเพียงการทดลองเชิงความคิด) กาลิเลโอได้แสดงให้เห็นว่าวัตถุที่เคลื่อนที่ภายใต้แรงโน้มถ่วงของโลกนั้นจะเคลื่อนที่โดยมีความเร่งเท่ากันไม่ว่าวัตถุนั้นจะมีมวลเท่าใดก็ตาม
เซอร์ไอแซก นิวตัน(Sir Isaac Newton ค.ศ. 1642 – 1726) นักคณิตศาสตร์และนักฟิสิกส์ชาวอังกฤษ เป็นบุคคลที่มีส่วนสำคัญในการศึกษาเกี่ยวกับแรงโน้มถ่วงเป็นอย่างมาก ทฤษฎีที่ทำให้เขามีชื่อเสียงมากที่สุด คือ การค้นพบกฎแรงดึงดูดของโลก (Law of Graitation) ซึ่งเขาได้ค้นพบทฤษฎีโดยบังเอิญ เหตุการณ์เกิดขึ้นในวันหนึ่งขณะที่นิวตันกำลังนั่งดูดวงจันทร์ แล้วก็เกิดความสงสัยว่าทำไมดวงจันทร์จึงต้องหมุนรอบโลก ในระหว่างที่เขากำลังนั่งมองดวงจันทร์อยู่เพลิน ๆ ก็ได้ยินเสียงแอปเปิ้ลตกลงพื้น เมื่อนิวตันเห็นเช่นนั้นก็ให้เกิดความสงสัยมากขึ้นไปอีกว่า ทำไมวัตถุต่าง ๆ จึงต้องตกลงสู่พื้นดินเสมอทำไมไม่ลอยขึ้นฟ้าบ้าง ซึ่งนิวตันคิดว่าต้องมีแรงอะไรสักอย่างที่ทำให้แอปเปิ้ลตกลงพื้นดิน จากความสงสัยข้อนี้เอง นิวตันจึงเริ่มการทดลองเกี่ยวกับแรงโน้มถ่วงของโลก การทดลองขั้นแรกของนิวตัน คือ การนำก้อนหินมาผูกเชือก จากนั้นก็แกว่งไปรอบ ๆ นิวตันสรุปจากการทดลองครั้งนี้ว่าเชือกเป็นตัวการสำคัญที่ทำให้ก้อนหินแกว่งไปมารอบ ๆ ไม่หลุดลอยไป ดังนั้นสาเหตุที่โลก ดาวเคราะห์ ต้องหมุนรอบดวงอาทิตย์ และดวงจันทร์ต้องหมุนรอบโลกต้องเกิดจากแรงดึงดูดที่ดวงอาทิตย์ที่มีต่อโลก และดาวเคราะห์ และแรงดึงดูดของโลกที่ส่งผลต่อดวงจันทร์ รวมถึงสาเหตุที่แอปเปิ้ลตกลงพื้นดินด้วยก็เกิดจากแรงดึงดูดของโลกด้วย
การเคลื่อนที่ของวัตถุในสนามโน้มถ่วง
การเคลื่อนที่ของวัตถุในสนามโน้มถ่วง คือ วัตถุที่อยู่ในสนามโน้มถ่วงของโลกจะถูกโลกดึงดูด ดังนั้นเมื่อปล่อยวัตถุให้ตกบริเวณใกล้ผิวโลกแรงดึงดูดของโลกจะทำให้วัตถุเคลื่อนที่เร็วขึ้นการตกของวัตถุที่มีมวลต่างกันในสนามโน้มถ่วงวัตถุจะเคลื่อนที่ด้วยความเร่งคงตัว เรียกว่า ความเร่งโน้มถ่วงมีทิศทางเข้าสู่ศูนย์กลางของโลก ความเร่งโน้มถ่วงที่ผิวโลก มีค่าต่างกันตามตำแหน่งทางภูมิศาสตร์ในการตกของวัตถุ วัตถุจะเคลื่อนที่ลงด้วยความเร่งโน้มถ่วง 9.8เมตรต่อวินาทียกกำลังสอง ถ้าโยนวัตถุขึ้นในแนวดิ่งวัตถุในสนามโน้มถ่วงจะเคลื่อนที่ขึ้นด้วยความเร่งโน้มถ่วง g โดยมีทิศเข้าสู่ศูนย์กลางโลก ทำให้วัตถุซึ่งเคลื่อนที่ขึ้นมีความเร็วลดลงวินาทีละ9.8เมตรต่อวินาที จนกระทั่งความเร็วสุดท้ายเป็นศูนย์
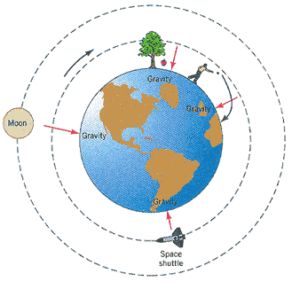นิยาม คือ วัตถุมวลอยู่ห่างจากมวลเป็นระยะให้แทนสนามความโน้มถ่วงของมวลที่ตำแหน่งของมวลสนามโน้มถ่วงจะมีขนาดเท่ากันและมีทิศทางพุ่งเข้าสู่มวล
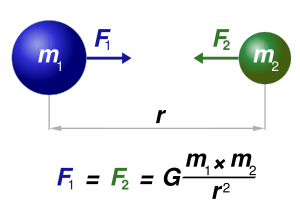
แรงโน้มถ่วงและสนามโน้มถ่วงของโลกคือแรงโน้มถ่วงที่โลกกระทำต่อวัตถุบนโลกคือน้ำหนัก (weight) ของวัตถุนั้น (น้ำหนักมีหน่วยเป็น นิวตัน) สำหรับวัตถุมวลบนผิวโลกจะมีน้ำหนักเท่ากับมีทิศเข้าสู่จุดศูนย์กลางโลกโดยที่ผิวโลกขนาดของ มีค่าประมาณ 9.8 m/s2
สูตร
| F | แทนความโน้มถ่วงระหว่างมวลทั้งสอง |
| G | แทนค่านิจโน้มถ่วงสากล |
| m1 | แทนมวลของวัตถุแรก |
| m2 | แทนมวลของวัตถุที่สอง |
| r | แทนระยะห่างระหว่างวัตถุทั้งสอง |
