จำนวนตรรกยะและอตรรกยะ
สมบัติของจำนวนตรรกยะ
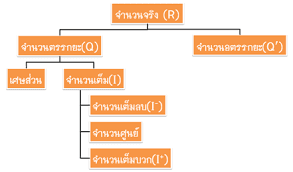
จำนวนตรรกยะ คือ จำนวนที่สามารถเขียนในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็มโดยที่ b ไม่เท่ากับ 0 จำนวนตรรกยะ จำแนกได้เป็น 3 ประเภท คือ
1. จำนวนเต็ม (Integer) ประกอบไปด้วยจำนวนธรรมชาติ จำนวนลบ และจำนวนศูนย์ เซตของจำนวนเต็มมักเขียนอยู่ในรูป Z ซึ่งมาจากคำว่า Zahlen (ภาษาเยอรมัน)
2. เศษส่วน (Fraction)
3. ทศนิยม (Repeating decimal)
ในทางคณิตศาสตร์ จำนวนตรรกยะ (หรือเศษส่วน) คืออัตราส่วนของจำนวนเต็มสองจำนวน มักเขียนอยู่ในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็ม และ b ไม่เท่ากับศูนย์
จำนวนตรรกยะแต่ละจำนวนสามารถเขียน
ได้ในรูปแบบที่หลากหลาย
| 1. จำนวนอตรรกยะ หมายถึง จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือทศนิยมซ้ำได้ ตัวอย่างเช่น √2 , √3, √5, -√2, – √3, -√5 หรือ ¶ ซึ่งมีค่า 3.14159265… | ||||||
| 2. จำนวนตรรกยะ หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ ตัวอย่างเช่น | ||||||
| • ระบบจำนวนตรรกยะ | ||||||
| จำนวนตรรกยะยังสามารถแบ่งเป็น 2 ประเภท คือ | ||||||
| 1. จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนหรือทศนิยมซ้ำได้ แต่ไม่เป็นจำนวนเต็ม ตัวอย่างเช่น | ||||||
| 2. จำนวนเต็ม หมายถึง จำนวนที่เป็นสมาชิกของเซต I = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …} เมื่อกำหนดให้ I เป็นเซตของจำนวนเต็ม | ||||||
| • ระบบจำนวนเต็ม | ||||||
| จำนวนเต็มยังสามารถแบ่งได้อีกเป็น 3 ประเภทด้วยกัน | ||||||
| 1. จำนวนเต็มลบ หมายถึง จำนวนที่เป็นสมาชิกของเซต I – โดยที่ I – = {…, -4, -3, -2, -1} เมื่อ I – เป็นเซตของจำนวนเต็มลบ |
||||||
| 2. จำนวนเต็มศูนย์ (0) | ||||||
| 3. จำนวนเต็มบวก หมายถึง จำนวนที่เป็นสมาชิกของเซต I+ โดยที่ I+ = {1, 2, 3, 4, …} เมื่อ I+ เป็นเซตของจำนวนเต็มบวก |
||||||
| จำนวนเต็มบวก เรียกได้อีกอย่างว่า “จำนวนนับ” ซึ่งเขียนแทนเซตของจำนวนนับได้ด้วยสัญลักษณ์ N โดยที่ N = I+ = {1, 2, 3, 4, …} ในทางคณิตศาสตร์ “…ตรรกยะ” หมายถึง เราจำกัดขอบเขตให้อยู่ในระบบจำนวนตรรกยะเท่านั้น เช่น พหุนามตรรกยะ
เซตของจำนวนตรรกยะทั้งหมดเราใช้สัญลักษณ์ Q หรือตัวใหญ่บนกระดานดำ โดยใช้เซตเงื่อนไข ได้ดังนี้
|
||||||
สรุป
สมบัติของจำนวนจริง
เนื่องจากว่า สมบัติของจำนวนจริงมีเยอะมาก ในที่นี้จะนำเสนอเฉพาะที่คิดว่าสำคัญแล้วกันนะครับ
ถ้าให้ a, b และ c เป็นจำนวนจริงใดๆ แล้ว จะได้ว่าจำนวนจริงจะมีสมบัติดังต่อไปนี้
1. สมบัติปิดการบวก: a+ b จะต้องเป็นจำนวนจริงเสมอ
2. สมบัติการเปลี่ยนหมู่ของการบวก: a + (b + c) = (a + b) + c
3. สมบัติการมีเอกลักษณ์การบวก: a + 0 = a = 0 + a โดยที่เราเรียก 0 ว่าเอกลักษณ์ของการบวก
4. สมบัติการมีอินเวอร์สของการบวก: a + (-a) = 0 = (-a) + a โดยที่ (-a) เป็นอินเวอร์สการบวกของ a
5. สมบัติปิดของการคูณ: a คูณ b หรือ ab จะต้องมีผลลัพธ์เป็นจำนวนจริงเสมอ
6. สมบัติการเปลี่ยนหมู่ของการคูณ: a(bc) = (ab) c
7. สมบัติการมีเอกลักษณ์การคูณ: a x 1 = a = 1 x a โดยที่เราเรียก 1 ว่าเอกลักษณ์ของการคูณ
8. สมบัติการมีอินเวอร์สของการคูณ: a a-1 = 0 = a-1 a โดยที่ a-1 เป็นอินเวอร์สการคูณของ a
9. สมบัติการแจกแจงทางซ้าย: a(b + c) = ab + ac
นอกจากสมบัติของจำนวนจริงแล้ว เรายังมีทฤษฎีบทเบื้องต้นสำหรับจำนวนจริงด้วย ในทำนองเดียวกับสมบัติของจำนวนจริง จะขอนำเสนอเฉพาะส่วนที่คิดว่าสำคัญเท่านั้นนะครับ
ถ้าให้ a, b, c และ d เป็นจำนวนจริงใดๆ จะได้ว่า
1. ถ้า a+c = b+c แล้ว a = b
2. ถ้า c ไม่เท่ากับศูนย์ และ ac =ab แล้ว a = b
3. เมื่อ c > 0 แล้วจะได้ว่า
(1) ถ้า a > b แล้ว ac > bc
(2) ถ้า a < b แล้ว ac < bc
(3) ถ้า ac > bc แล้ว a > b
(4) ถ้า ac < bc แล้ว a < b
4. เมื่อ c < 0 แล้วจะได้ว่า
(1) ถ้า a > b แล้ว ac < bc
(2) ถ้า a < b แล้ว ac > bc
(3) ถ้า ac > bc แล้ว a < b
(4) ถ้า ac < bc แล้ว a > b
5. ถ้า ab = 0 แล้ว a = 0 หรือ b = 0
6. ถ้า a < b และ c < d แล้ว a – d < b – c






