ตรรกศาสตร์เบื้องต้นเรื่องตัวบ่งปริมาณ
ตัวบ่งปริมาณ(Quantified statement)
ตัวบ่งปริมาณในตรรกศาสตร์ มี 2 ชนิด คือ
1) ตัวบ่งปริมาณ “ทั้งหมด” หมายถึงทุกสิ่งทุกอย่างที่ต้องการพิจารณาในการ
นำไปใช้อาจใช้คำอื่นที่มีความหมายเช่นเดียวกับ “ทั้งหมด” ได้ ได้แก่ “ทุก”
“ทุก ๆ” “แต่ละ” “ใด ๆ” ฯลฯ เช่น คนทุกคนต้องตาย, คนทุก ๆ คนต้องตาย,
คนแต่ละคนต้องตาย, ใคร ๆ ก็ต้องตาย
2) ตัวบ่งปริมาณ “บาง” หมายถึงบางส่วนหรือบางสิ่งบางอย่างที่ต้องการ
พิจารณา ในการนำไปใช้อาจใช้คำอื่นที่มีความหมายเช่นเดียวกันได้ ได้แก่
“บางอย่าง” “มีอย่างน้อยหนึ่ง” เช่น สัตว์มีกระดูกสันหลังบางชนิดออกลูกเป็น
ไข่, มีสัตว์มีกระดูกสันหลังอย่างน้อยหนึ่งชนิดที่ออกลูกเป็นไข่
ทฤษฎีตรรกสมมูล (Logical Equivalences)
ความรู้ประพจน์ตรรกะสมมูล (Logical equivalent statement)มีประโยชน์มากสำหรับการหาข้อโต้แย้งและข้อสรุปในทางคณิตศาสตร์ ซึ่งในทางปฏิบัติแล้วการสรุปเหตุผลในแต่ละรูปจะยุ่งยากมากหากไม่อาศัยทฤษฎี ตรรกะสมมูลในการกล่าวอ้าง ดังนั้นจึงสรุปทฤษฎีตรรกะสมมูลไว้สำหรับใช้อ้างอิงต่อไป
กำหนดให้ p , q , r แทนประพจน์ใดๆ t แทนสัจนิรันดร์ c แทนความขัดแย้ง
- กฎการสลับที่ (Commutative laws)
p ^ q = q ^p , p ^ q = q v p - กฎการเปลี่ยนหมู่ (Associative laws)
(p ^ q)^r = p ^ (q ^ r) , (p ^ q) v r = p v (q ^ r) - กฎการแจกแจง (Distributive laws)
p ^ (q v r)= (p ^ q) v ( p ^ r) ,
p v (q ^ r) = (p v q) ^ ( p v r) - กฎเอกลักษณ์ (Identity laws)
p v t = t , p ^ t = p - กฎนิเสธ (Negative laws)
p v ~p = t , p ^ ~ p = c
6.กฎนิเสธซ้อนนิเสธ (Double negative laws)
~(~p) = p
- กฎนิจพล (Idempotent laws)
p ^p = p , p = p - กฎของเดอมอเกน (demerger’s laws)
~(p ^q)= ~p v ~q , ~(p v q) = ~p v ~q - กฎการจำกัดขอบข่าย (Universal bound laws)
p v t = t , p ^ c = c - กฎการซึมซับ (Absorption laws)
p v (p ^ q)= p , p ^ (p v q) = p - นิเสธของc และ t
~t = c , ~c=t
ตัวบ่งปริมาณ(Quantified statement)
ตัวบ่งปริมาณในตรรกศาสตร์ มี 2 ชนิด คือ
1) ตัวบ่งปริมาณ “ทั้งหมด” หมายถึงทุกสิ่งทุกอย่างที่ต้องการพิจารณาในการ
นำไปใช้อาจใช้คำอื่นที่มีความหมายเช่นเดียวกับ “ทั้งหมด” ได้ ได้แก่ “ทุก”
“ทุก ๆ” “แต่ละ” “ใด ๆ” ฯลฯ เช่น คนทุกคนต้องตาย, คนทุก ๆ คนต้องตาย,
คนแต่ละคนต้องตาย, ใคร ๆ ก็ต้องตาย
2) ตัวบ่งปริมาณ “บาง” หมายถึงบางส่วนหรือบางสิ่งบางอย่างที่ต้องการ
พิจารณา ในการนำไปใช้อาจใช้คำอื่นที่มีความหมายเช่นเดียวกันได้ ได้แก่
“บางอย่าง” “มีอย่างน้อยหนึ่ง” เช่น สัตว์มีกระดูกสันหลังบางชนิดออกลูกเป็น
ไข่, มีสัตว์มีกระดูกสันหลังอย่างน้อยหนึ่งชนิดที่ออกลูกเป็นไข่
ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ
1.∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง
2. ∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ
3. ∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง
4.∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง
การให้เหตุผล (Reasoning)โดยทั่วไปกระบวนการให้เหตุผลมี 2 ลักษณะคือ1.การให้เหตุผลแบบนิรนัย เป็นการให้เหตุ โดยนำข้อความที่กำหนดให้ ซึ่งต้องยอมรับว่าเป็นจริง ทั้งหมด เรียกว่า เหตุ และข้อความจริงใหม่ที่ได้เรียกว่า ผลสรุป ซึ่งถ้า พบว่าเหตุที่กำหนดนั้นบังคับให้เกิดผลสรุปไม่ได้ แสดงว่า การให้เหตุผลดังกล่าวสมเหตุสมผล แต่ถ้าพบว่าเหตุที่กำหนดนั้นบังคับให้เกิดผลสรุปไม่ได้แสดงว่า การให้เหตุผลดังกล่าวไม่สมเหตุสมผล
สมมูลและนิเสธของประโยคที่มีตัวบ่งปริมาณ
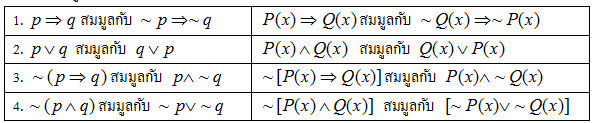

จากสมมูลของประโยคเปิดดังกล่าว ถ้าเติมตัวบ่งปริมาณชนิดเดียวกันไว้ข้างหน้าจะได้ประพจน์ที่สมมูลกันด้วยเช่น

เนื่องจากประโยคที่มีตัวบ่งปริมาณเป็นประพจน์ ดังนั้น สามารถเทียบรูปแบบที่สมมูลกับรูปแบบประพจน์ที่สมมูลกันได้ เช่น








