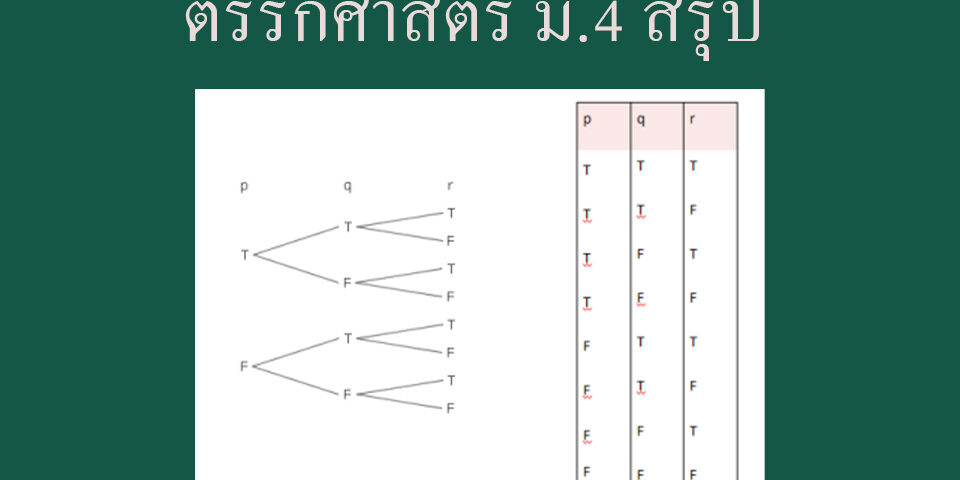
การสร้างตารางงค่าความจริง
พิจารณาประพจน์ที่มีตัวเชื่อม เช่น ~p, – p Λ q, – p q, – p → q, – p ↔ q, – (p Λ q) → r จะเห็นว่าประพจน์เหล่านี้มี p, q, r เป็นประพจน์ย่อย ซึ่งเรายังไม่กำหนดค่าความจริง จะเรียก p, q, r ว่า เป็นตัวแปรแทนประพจน์ใดๆ และเรียกประพจน์ที่มีตัวเชื่อม เช่น ~p, – p Λ q, – p q, – p → q, -p ↔ q ว่า รูปแบบของประพจน์ เนื่องจาก p, q, r เป็นตัวแปรแทนประพจน์ใดๆ ดังนั้น ในการพิจารณาค่าความจริงของรูปแบบของประพจน์จึงต้องกำหนดค่าความจริงของประพจน์ย่อยทุกกรณีที่เป็นไปได้ เช่น
- ถ้ามีประพจน์เดียวคือ p มีกรณีเกี่ยวกับค่าความจริงที่จะพิจารณา 2 กรณี
- ถ้ามีสองประพจน์คือ p และ q มีกรณีเกี่ยวกับค่าความจริงที่จะพิจารณา 4 กรณี
ในทำนองเดียวกัน ถ้ามีสามประพจน์คือ p, q และ r มีกรณีเกี่ยวกับค่าความจริงที่จะพิจารณา ทั้งหมด 8 กรณี ดังนี้
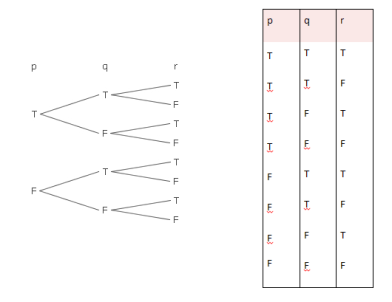
ตารางค่าความจริง p q
ถ้ามีจำนวนประพจน์มากกว่านี้ การหากรณีทั้งหมดที่จะพิจารณาก็หาได้ในทำนองเดียวกัน
| ตัวอย่างที่ 1 | กำหนดให้ p และ q เป็นประพจน์ จงสร้างตารางค่าความจริงของ (p → q) → (~p Λ ~q) |
| วิธีทำ | รูปแบบของประพจน์ (p → q) → (~p Λ ~q) ประกอบด้วย ประพจน์ย่อยสองประพจน์ คือ p, q จึงมีกรณีเกี่ยวกับค่าความจริงที่ | ||||||||||||||
| อาจเกิดขึ้นได้ทั้งหมด 4 กรณี จะได้ตารางค่าความจริงของ (p → q) → (~p Λ ~q) ดังนี้ | |||||||||||||||
|
| ตัวอย่างที่ 2 | กำหนดให้ p, q และ r เป็นประพจน์ จงสร้างตารางค่าความจริงของ (p Λ q) → r |
| วิธีทำ | รูปแบบของประพจน์ (p Λ q) → r ประกอบด้วย ประพจน์ย่อยสามประพจน์ คือ p, q และ r จึงมีกรณีเกี่ยวกับค่าความจริงที่อาจ | ||||||||||
| เกิดขึ้นได้ทั้งหมด 8 กรณี จะได้ตารางค่าความจริงของ (p Λ q) → r ดังนี้ | |||||||||||
|
| ตัวอย่างที่ 3 | กำหนดให้ p, q และ r เป็นประพจน์ จงสร้างตารางค่าความจริงของ p Λ (~q) กับ ~(p → q) |
| วิธีทำ | จะได้ตารางค่าความจริงของ p Λ (~q) กับ ~(p → q) ดังนี้ | ||||||||||||
|
|||||||||||||
| จากตารางค่าความจริงนี้ จะเห็นว่า ค่าความจริงของ p Λ (~q) กับ ~(p → q) ตรงกันกรณีต่อกรณี |