ความคิดเกี่ยวกับตรีโกณมิติในชีวิตประจำวัน
มนุษย์กับสิ่งแวดล้อมมีความสัมพันธ์ต่อกัน มนุษย์สังเกตปรากฎการณ์ทางธรรมชาติต่าง ๆ โดยเฉพาะในเรื่องดาราศาสตร์ เพราะเป็นเรื่องที่พบเห็นทุกวัน เริ่มตั้งแต่การขึ้น ตก ของดวงอาทิตย์ ดวงจันทร์ และดวงดาวต่าง ๆ หากเราสังเกตการเปลี่ยนแปลงของตำแหน่งดวงดาวต่าง ๆ เมื่อเทียบกับเวลาต่าง ๆ ในรอบปี เราจะพบกับสิ่งที่ชวนคิดหลาย ๆ อย่าง เช่น ดวงอาทิตย์ขึ้นตำแหน่งเดียวกันตลอดทั้งปีหรือไม่ ทำไมแต่ละวันดวงอาทิตย์จึงขึ้นจากขอบฟ้าไม่ตรงเวลาเดียวกัน ความคิดในเรื่องทรงกลมท้องฟ้าที่มองเห็นทำให้เกิดจินตนาการ และหาหนทางเรียนรู้ โดยใช้วิชาการทางคณิตศาสตร์
ต้นตำรับความคิดทางตรีโกณมิติ จึงมาจากสามเหลี่ยมทรงกลมท้องฟ้า ความสำคัญในเรื่องการคำนวณเกี่ยวข้องกับทรงกลมมีมาก่อนการนำมาใช้ในเรื่องสามเหลี่ยมแนวราบ โดยสามารถนำเอาหลักการทางตรีโกณมิติมาใช้แก้ปัญหาภายหลัง
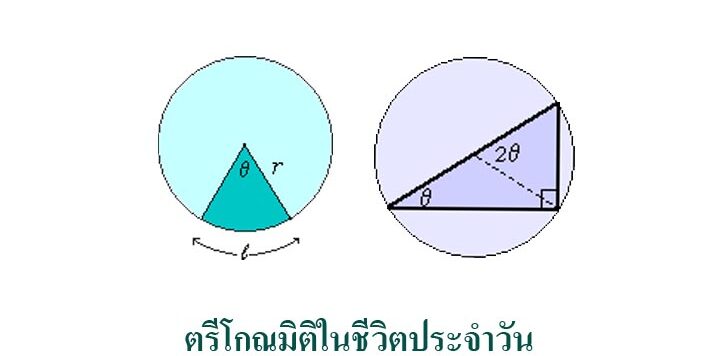
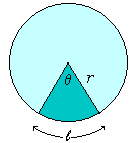
ความผูกพันในเรื่องทรงกลมในสมัยเริ่มต้นมีหลักฐานว่า ฮิปพาร์ชุส (Hipparchus) ได้เขียนตารางตรีโกณมิติไว้ตั้งแต่เมื่อ 140 ปี ก่อนคริสตกาล ตารางการคำนวณในสมัยนั้นเน้นการหาความยาวส่วนโค้งของวงกลม เมื่อวงกลมมีรัศมีหนึ่งหน่วย จากตารางที่แสดงให้เห็นว่า เมื่อค่า θ มีค่าต่าง ๆ กัน ค่าของส่วนโค้งจะแปรเปลี่ยนไป และสิ่งที่น่าสนใจคือค่าของ ![]() ที่ได้มีค่าเท่ากับ 2sin(θ/2) ตารางที่ฮิปพาร์ชุสเขียนไว้ได้สูญหายไปหมด ซึ่งจะเห็นว่า ตัวเลขที่เป็นธรรมชาติมีหลายตัว และมีการค้นคว้ากันมาเรื่อย ๆ ต่อมามีการแบ่งมุมรอบจุดศูนย์กลางของวงกลมเป็น 360 องศา และจากแนวความคิดนี้ พโทเลมีนำเอามุม 360 องศา และแบ่งเส้นผ่านศูนย์กลางเป็นส่วน 120 ส่วน และคำนวณอัตราส่วน
ที่ได้มีค่าเท่ากับ 2sin(θ/2) ตารางที่ฮิปพาร์ชุสเขียนไว้ได้สูญหายไปหมด ซึ่งจะเห็นว่า ตัวเลขที่เป็นธรรมชาติมีหลายตัว และมีการค้นคว้ากันมาเรื่อย ๆ ต่อมามีการแบ่งมุมรอบจุดศูนย์กลางของวงกลมเป็น 360 องศา และจากแนวความคิดนี้ พโทเลมีนำเอามุม 360 องศา และแบ่งเส้นผ่านศูนย์กลางเป็นส่วน 120 ส่วน และคำนวณอัตราส่วน
ของเส้นรอบรูปต่อเส้นผ่านศูนย์กลางได้ค่าเป็น π ในยุคแรก ๆ กำหนดให้มีค่าโดยประมาณเท่ากับ 3
ความคิดเชิงทฤษฎีเรขาคณิตจึงเกิดขึ้นอย่างต่อเนื่อง มีการสร้างทฤษฎีทางเรขาคณิตที่ว่าด้วย เส้น มุม ส่วนโค้งของวงกลม ทำให้การคำนวณเจริญก้าวหน้ามาเป็นลำดับ
ตัวเลขธรรมชาติที่เกี่ยวกับ sin x cos x และ tan x จึงเป็นที่รู้จักกันแพร่หลายและนำมาใช้ประโยชน์ พโทเลมียังทราบความสัมพันธ์ของ sin2x + cos2x = 1 และสามารถพิสูจน์ความจริงนี้ได้
จากความคิดในเรื่องส่วนโค้งของวงกลมและรัศมี ทำให้การคิดคำนวณหาค่าของสัดส่วนทางตรีโกณมิติ ในเวลาต่อมาในรูปของด้านของสามเหลี่ยมมุมฉาก ซึ่งก็คือสัดส่วนของด้านต่างๆ และพิจารณาเฉพาะสามเหลี่ยมมุกฉาก
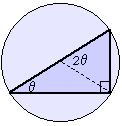
เท่านั้น ทำให้วิชาตรีโกณมิติสมัยใหม่จึงเน้นเฉพาะรูปสามเหลี่ยม ซึ่งมีสัดส่วนที่สำคัญเช่นเดียวกับหลักการทางด้านวงกลม และส่วนโค้ง คือ
| ค่าของ sinθ | คือ | อัตราส่วนระหว่างด้านตรงข้ามมุม กับด้านตรงข้ามมุมฉาก |
| ค่าของ cosinθ | คือ | อัตราส่วนระหว่างด้านประชิดมุม กับด้านตรงข้ามมุมฉาก |
| ค่าของ tangentθ | คือ | อัตราส่วนระหว่างด้านตรงข้ามมุม กับด้านประชิดมุม |
การใช้งานจึงเน้นไปที่เรขาคณิต และการหาผลลัพธ์ของมุมและเส้นที่มีพัฒนาการต่อเนื่องและนำมาใช้ในชีวิตประจำวัน
ลองนึกดูว่าชีวิตความเป็นอยู่ของเราเกี่ยวกับรูปทรงเรขาคณิตอยู่มาก ทฤษฎีที่เกี่ยวกับรูปทรงเรขาคณิต เป็นเรื่องที่มีมานานแล้ว และมีการนำมาประยุกต์ใช้งานได้มากมาย