ตรีโกณมิติ การวัดมุมในหน่วยองศา-การแปลงหน่วยเรเดียนและองศา

ตรีโกณมิติ

การวัดมุมในหน่วยองศา

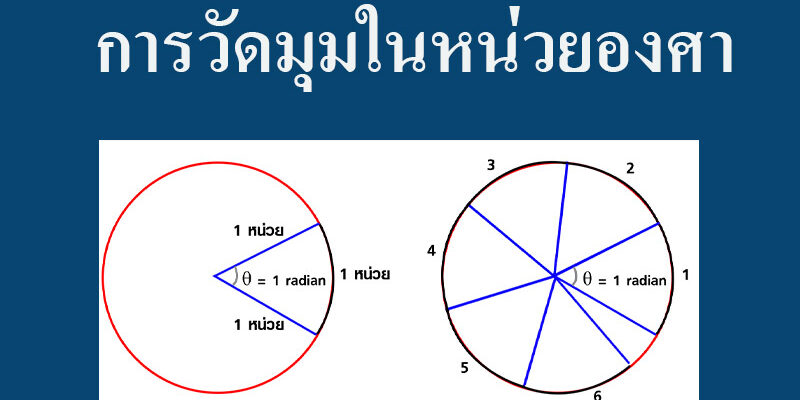
เรเดียนก็คือ อัตราส่วนระหว่าง ส่วนโค้งของวงกลมกับรัศมี หรือก็คือ θ = ส่วนโค้งของวงกลม/รัศมี หน่วยจึงหายไป ดังนั้น เรเดียนจึงไม่มีหน่วย หากสมมุติให้รัศมีวงกลมมีค่า 1 หน่วย ส่วนโค้งของวงกลมที่มีระยะจากรัศมีเส้นที่ 1 มายังรัศมีเส้นที่ 2 มีความยาว 1 หน่วยเท่ากับขนาดของรัศมี θ ก็จะมีค่าเท่ากับ 1 และเมื่อลองแบ่งวงกลมไปเรื่อย ๆ ทีละ θ = 1 จะได้มุมภายในวงกลมทั้งหมดเป็น  θ = 6 และเหลือส่วนโค้งของวงกลมอีกเล็กน้อย

เราสามารถหาส่วนโค้งของวงกลมที่เหลืออยู่อีกเล็กน้อยได้จากสูตรเส้นรอบวง = 2πr และนิยาม θ = ส่วนโค้งของวงกลม/รัศมี
ซึ่งจะได้เป็น θ = 2πr/r
ดังนั้น θ = 2π
แต่ π = 3.14 หรือ 22/7 จึงได้เป็น θ = 2π = 2×3.14
ด้วยเหตุนี้ θ หรือมุมภายในวงกลมทั้งหมดจึงเท่ากับ 6.28 ซึ่งทำให้เราทราบว่า ส่วนโค้งของวงกลมที่เหลืออีกเล็กน้อยนั่นก็คือ 0.28

การแปลงหน่วยเรเดียนและองศา

หากมุมภายในวงกลมทั้งหมดเป็น θ = 2π เมื่อเทียบกับหน่วยองศา จะเท่ากับ 360 องศา
ดังนั้น π = 180 องศา

หากต้องการทราบว่า 1 เรเดียนเป็นกี่องศา เราสามารถหาได้โดยการเทียบบัญญัติไตรยางค์
π เรเดียน เท่ากับ 180 องศา
ดังนั้น 1 เรเดียน เท่ากับ 180/π = 57.3 องศา

หากต้องการทราบว่า 1 องศาเป็นกี่เรเดียน เราสามารถหาได้โดยการเทียบบัญญัติไตรยางค์
180 องศา เท่ากับ π หรือ 3.14 เรเดียน
ดังนั้น 1 องศา เท่ากับ 3.14/180 = 0.0174 เรเดียน
หรือ ต้องการทราบว่า 120 องศา เป็นกี่เรเดียน เราสามารถหาได้โดยการเทียบบัญญัติไตรยางค์
180 องศา เท่ากับ π หรือ 3.14 เรเดียน
ดังนั้น 120 องศา เท่ากับ (πx120)/180 = 2π/3 หรือ 2.094 เรเดียน