ตัวประกอบของจำนวนนับ

  ตัวประกอบ หมายถึง จำนวนนับที่หารจำนวนนับที่เรากำหนดให้ได้ลงตัว เช่น a จะเป็นตัวประกอบของ b ก็ต่อเมื่อ b หารด้วย a ลงตัว หรือกล่าวอีกนัยหนึ่งก็คือ a หาร b ลงตัว
ตัวอย่าง
30 หารด้วย 6 ลงตัว แสดงว่า 6 เป็นตัวประกอบของ 30 ในขณะที่ 30 หารด้วย 4 ไม่ลงตัว แสดงว่า 4 ไม่เป็นตัวประกอบของ 30 เป็นต้น
    หรือ
จำนวนที่หาร 18 ลงตัวประกอบด้วย 1 , 2 , 3 , 6 , 9 , 18 แสดงว่า 1 , 2 , 3 , 6 , 9 , 18 เป็นตัวประกอบของ 18
 จำนวนเฉพาะ หมายถึง จำนวนที่มีตัวประกอบเพียง 2 ตัว คือ 1 กับตัวของมันเอง
การหาตัวประกอบของจำนวนนับใด ๆ จะพบว่า บางจำนวนที่ตัวประกอบเพียง 1 ตัว บางจำนวนมีตัวประกอบ 2 ตัว ในขณะที่บางตัวมีตัวประกอบมากกว่า 2 ตัว
1 มีตัวประกอบ 1 ตัว คือ 1
6 มีตัวประกอบ 4 คือ 1 , 2 , 3 , 6
2 มีตัวประกอบ 2 คือ 1 , 2 หรืออีกนัยหนึ่งว่า 2 มีตัวประกอบ 2 คือ 1 กับ ตัวของมันเอง
3 มีตัวประกอบ 2 คือ 1 , 3 หรืออีกนัยหนึ่งว่า 3 มีตัวประกอบ 2 คือ 1 กับ ตัวของมันเอง
จากตัวอย่างด้านบน เราพบว่า 1 มีตัวประกอบ 1 ตัว 6 มีตัวประกอบ 4 ตัว ในขณะที่ 2 และ 3 มีตัวประกอบ 2 ตัว คือ 1 กับ ตัวของมันเอง เราเรียกจำนวนที่มีตัวประกอบเพียง 2 ตัวนี้ว่า จำนวนเฉพาะ
ตัวประกอบเฉพาะ ตัวประกอบของจำนวนนับใดที่เป็นจำนวนเฉพาะ
การหาตัวประกอบเฉพาะของจำนวนนับใด ๆ นั้น เราจะต้องหาตัวประกอบทั้งหมดของจำนวนนับนั้น ๆก่อน จากนั้นจึงค่อยพิจารณา ตัวประกอบเหล่านั้นว่า มีจำนวนใดเป็นจำนวนเฉพาะบ้าง ซึ่งจำนวนเฉพาะเหล่านั้นเราเรีนกว่า ตัวประกอบเฉพาะ
    ตัวอย่าง
ตัวประกอบของ 12 ประกอบ 1 , 2 , 3 , 4 , 6 , 12
ตัวประกอบเฉพาะของ 12 ประกอบด้วย 2 , 3
ทั้งนี้เพราะว่า 2 , 3 เป็นตัวประกอบของ 12 และเป็นจำนวนเฉพาะด้วย

ตัวประกอบเฉพาะ คือ ตัวประกอบของจำนวนนับที่เป็นจำนวนเฉพาะ
ตัวประกอบ คือ จำนวนนับใดๆที่หารจำนวนนับนั้นลงตัวเช่น ตัวประกอบของ 10 คือ 1 , 2 , 5และ10
ตัวหารร่วมมาก คือ จำนวนนับใดๆที่เป็นตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับนั้น
เขียนย่อคือ ห.ร.ม. เช่น ตัวประกอบร่ามมากสุดของ 16 และ 24 คือ 8
จำนวนเฉพาะ คือ จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียงสองตัวเท่านั้นได้แก่ 1 และตัวมันเอง เช่น จำนวนเฉพาะที่อยู่ระหว่าง 1 ถึง 10 คือ 2 , 3 , 5 , 7
การแยกตัวประกอบ คือ ประโยคที่แสดงการเขียนจำนวนนับนั้นในรูปการคูณของตัวประกอบ เฉพาะ เช่น ตัวประกอบของ 12 คือ 2 * 2 * 3
ตัวคูณร่วมน้อย คือ จำนวนนับใดๆที่เป็นตัวประกอบร่วมที่มีค่าน้อยที่สุดของจำนวนนับ
เขียนย่อคือ ค.ร.น. เช่น ตัวคูณร่วมน้อยของ 4 และ 6 คือ 12 ตัวประกอบของจำนวนนับ จำนวนที่นักเรียนพบเห็นในชีวิตประจำวันอยู่เสมอๆได้แก่ 1,2,3,4,……ไม่มีที่สิ้นสุด เรียกจำนวนเหล่านี้ว่า จำนวนนับ หรือ จำนวนธรรมชาติ หรือ จำนวนเต็มบวก จงพิจารณาตารางต่อไปนี้

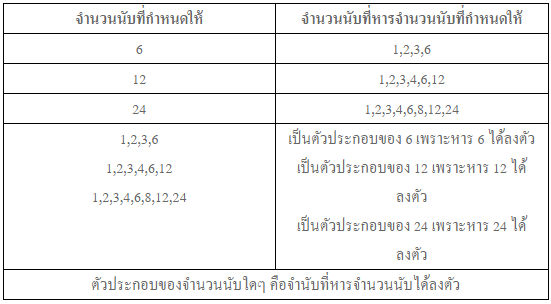
การแยกตัวประกอบ จงพิจารณาตารางต่อไปนี้

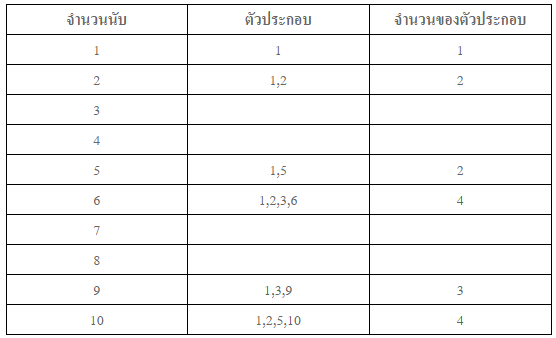
จากตารางข้างต้น  จะเห็นว่าจำนวนนับที่กำหนดให้แต่ละจำนวน  สามารถเขียนในรูปการคูณได้หลวกหลาย
พิจารณาแบบที่ 2 จะเห็นว่า
8 = 2 x 2 x 2  ตัวคูณ คือ 2  แต่ละจำนวนเป็นตัวประกอบ
                        12 = 2 x 2 x 3  ตัวคูณ คือ 2 และ 3  แต่ละจำนวนเป็นตัวประกอบ
เช่นเดียวกัน  20 = 2 x 2 x 5 ตัวคูณ คือ 2 และ 5  แต่ละจำนวนเป็นตัวประกอบ
เราเรียกประโยค  8 = 2 x 2 x 2 ว่าเป็นการแยกตัวประกอบของ 8
12 = 2 x 2 x 3 ว่าเป็นการแยกตัวประกอบของ 12
20 = 2 x 2 x 5 ว่าเป็นการแยกตัวประกอบของ 20
                การแยกตัวประกอบของจำนวนนับใด คือ ประโยคที่แสดงการเขียนจำนวนนับในรูปการคูณของตัวประกอบเฉพาะ ประโยค  28 = 2 x 2 x 7  แสดงการเขียน 28 ในการคูณของตัวประกอบเฉพาะเราเรียกประโยคนี่ว่า  การแยกตัวประกอบของ 28
ตัวอย่าง  จงแยกตัวประกอบของ 225
วิธีทำ                      225 = 3 x 3 x 5 x 5

ตัวหารร่วมมาก  หรือ ห.ร.ม (Greatest  common  divisor: G.C.D)
การหารร่วมมาก ที่จะกล่าวต่อไปนี้จะนำเสนอวิธีการหารเพียง 3 วิธีเท่านั้น  คือ การหาร ห.ร.ม โดยวิธีการพิจารณาตัวประกอบ การหา ห.ร.ม โดยการแยกตัวประกอบ  และการหา ห.ร.ม โดยการตั้งหาร
(หารสั้น) เราจะยกตัวอย่างการหา ห.ร.ม โดยวิธีการพิจารณาตัวประกอบเท่านั้น
การหา ห.ร.ม โดยวิธีการพิจารณาตัวประกอบ
           พิจารณาตัวประกอบของ 12 และ 18 มาเขียนแสดงความสัมพันธ์ใหม่ ดังนี้
ตัวประกอบของ 12 คือ 1,2,3, และ 4,6,12
ตัวประกอบของ 18 คือ 1,2,3, และ 6,9,18
ตัวประกอบร่วม( Common factor ) ของ 12 และ 18 ได้แก่ 1,2,3,6

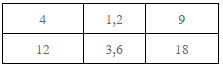
ตัวประกอบร่วมของ 12 และ 18 ที่มากที่สุดได้แก่ 6
เรียกตัวประกอบร่วมที่มากที่สุดว่า  ตัวหารร่วมมาก 
ดังนั้น 6 เป็นตัวหารร่วมมากของ 12 และ 18 หรือ 6 เป็น ห.ร.ม ของ 12 และ 18
ตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับนั้น เรียกว่า ตัวหารร่วมมาก (ห.ร.ม)
สรุป   การหา ห.ร.ม โดยวิธีการพิจารณาตัวประกอบ ทำได้โดยหาตัวประกอบร่วมของทุกจำนวนและ
พิจารณาตัวประกอบร่วมที่มากที่สุด ห.ร.ม ของจำนวนนับคือ  ตัวประกอบร่วมที่มากที่สุด
ตัวอย่าง  จงหา  ห.ร.ม ของ 18 และ 48
วิธีทำ    ตัวประกอบของ 18 ได้แก่ 1,2,3,6,9 และ 18
ตัวประกอบของ 48 ได้แก่ 1,2,3,4,6,8,12,16,24 และ 48
                ตัวประกอบร่วมของ 18 และ 48 ได้แก่ 1,2,3,6
                ตัวประกอบร่วมของ 18 และ 48 ที่มากที่สุดได้แก่ 6
ดังนั้น ห.ร.ม ของ 18 และ 48 คือ 6 

การคูณร่วมน้อย หรือ ค.ร.น (Least  common  multiple: L.C.M)
การหาตัวคูณร่วมน้อย ที่กล่าวต่อไปนี้จะนำเสนอวิธีการหาเพียง 3 วิธีเท่านั้น  คือการหา ค.ร.น โดยวิธีการพิจารณาพหุคูณ  การหา ค.ร.น โดยการแยกตัวประกอบและการหา 8 ค.ร.น โดยการแยกตัวประกอบและการหา ค.ร.น  โดยการตั้งหาร( หารสั้น ) ในที่นี่จะยกตัวอย่างกรณีเดี๋ยว คือ
การหา ค.ร.น โดยวิธีการพิจารณาพหุคูณ
ให้นักเรียนช่วยกันพิจารณา  ดังนี้
พหุคูณของ 3 คือ 3,6,9,12,15,18,21,24,30,33,36,…
                พหุคูณของ 5 คือ 5,10,15,20,25,30,35,40,45,50,….
                พหุคูณร่วมของ 3 และ 5 ได้แก่ 15,30,45,….
                พหุคูณร่วมน้อยที่สุดของ 3 และ 5 ได้แก่ 15
                เรียกพหุคูณที่น้อยที่สุดว่า ตัวคูณร่วมน้อย
ดังนั้น 15 เป็นตัวคูณร่วมน้อยของ 3 และ 15
                เขียนย่อๆว่า 15 เป็น ค.ร.น ของ 3 และ 5
สรุป     การหา ค.ร.น โดยวิธีพิจารณาพหุคูณทำได้โดยหาจำนวนที่มีจำนวนที่กำหนดให้เป็นตัวประกอบ  แล้วพิจารณาจำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ ค.ร.น ของจำนวนนั้น  คือ จำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ

การแยกตัวประกอบ หมายถึง การเขียนในรูปการคูณของตัวประกอบเฉพาะของจำนวนนับนั้น ๆ
ตัวอย่าง
12 สามารถแยกตัวประกอบได้เป็น 2 x 2 x 3
จากตัวอย่างจะพบว่า 2 และ 3 เป็นตัวประกอบเฉพาะของ 12 ซึ่งอาจมีการคูณซ้ำกันหลายครั้งก็ได้ และการคูณซ้ำกันหลายครั้ง สามารถเขียนในรูปของเลขยกกำลังได้ กล่าวคื อเราจะแยกตัวประกอบของ 12 เป็น x 3 แทน 2 x 2 x 3 ก็ได้ (2² อ่านว่า 2 ยกกำลัง 2 )
ตัวอย่างเพิ่มเติม
75 สามารถแยกตัวประกอบได้เป็น 5 x 5 x 3 หรือ 5² x 3
100 สามารถแยกตัวประกอบได้เป็น 5 x 5 x 2 x 2 หรือ 5²x 
การแยกตัวประกอบสามารถกระทำได้ดังนี้
วิธีที่ 1 วิธีเขียนในรูปกระจายของผลคูณของตัวประกอบ
การแยกตัวประกอบโดยวิธีนี้ เป็นการนำจำนวนนับที่กำหนดมาเขยนในรูปผลคูณของตัวประกอบทีละ 2 จำนวน โดยเขียนไปเรื่อย ๆ จนกระทั่งกลายเป็นผลคูณของตัวประกอบเฉพาะ
ตัวอย่าง จงแยกตัวประกอบของ 80
80 = 8 x 10
= 2 x 4 x 2 x 5
= 2 x 2 x 2 x 2 x 5
ดังนั้น 80 = 2 x 2 x 2 x 2 x 5
                       หรือ  80 = 2⁴x 5
  วิธีที่ 2 วิธีตั้งหาร
การแยกตัวประกอบโดยวิธีตั้งหาร ใช้วิธีหารสั้น ซึ่งมีขั้นตอนง่าย ๆดังนี้
1) หารจำนวนนับที่กำหนดให้ด้วยตัวประกอบเเฉพาะของมัน
2) หารผลหารที่ได้จากข้อ 1 ด้วยตัวประกอบเฉพาะ
3) ดำเนินการเช่นเดียวกับข้อ 2 จนกระทั่งผลหารสุดท้ายมีค่าเท่ากับ 1
4) นำตัวหารทั้งหมดคูณกัน จะกลายเป็นการแยกตัวประกอบของจำนวนในข้อ 1
ตัวอย่าง จงแยกตัวประกอบของ 80
2 )80  
2 )40  
2 )20  
2 )10  
5 ) 5  
 1
ดังนั้น 80 = 2 x 2 x 2 x 2 x 5
                       หรือ  80 = 2⁴x 5

ตัวประกอบของ 6 มีทั้งหมดกี่จำนวน ? จำนวนใดบ้าง ?

เลข 1 เป็นตัวประกอบของ 6 หรือไม่ ?

	ทดสอบโดยนำ 1 ไปหาร 6 ถ้าหารลงตัว แสดงว่า 1 เป็นตัวประกอบของ 6
	6 ÷ 1 หารลงตัว ได้ผลหารคือ 6 ดังนั้น 1 เป็นตัวประกอบของ 6
	6 ÷ 1 = 6 → 6 = 1 x 6

เลข 2 เป็นตัวประกอบของ 6 หรือไม่ ?

	ทดสอบโดยนำ 2 ไปหาร 6 ถ้าหารลงตัว แสดงว่า 2 เป็นตัวประกอบของ 6
	6 ÷ 2 หารลงตัว ได้ผลหารคือ 3 ดังนั้น 2 เป็นตัวประกอบของ 6
	6 ÷ 2 = 3 → 6 = 2 x 3

เลข 3 เป็นตัวประกอบของ 6 หรือไม่ ?

	ทดสอบโดยนำ 3 ไปหาร 6 ถ้าหารลงตัว แสดงว่า 3 เป็นตัวประกอบของ 6
	6 ÷ 3 หารลงตัว ได้ผลหารคือ 2 ดังนั้น 3 เป็นตัวประกอบของ 6
	6 ÷ 3 = 2 → 6 = 3 x 2

เลข 4 เป็นตัวประกอบของ 6 หรือไม่ ?

	ทดสอบโดยนำ 4 ไปหาร 6 ถ้าหารลงตัว แสดงว่า 4 เป็นตัวประกอบของ 6
	6 ÷ 4 หารไม่ลงตัว ดังนั้น 4 ไม่เป็นตัวประกอบของ 6

เลข 5 เป็นตัวประกอบของ 6 หรือไม่ ?

	ทดสอบโดยนำ 5 ไปหาร 6 ถ้าหารลงตัว แสดงว่า 5 เป็นตัวประกอบของ 6
	6 ÷ 5 หารไม่ลงตัว ดังนั้น 5 ไม่เป็นตัวประกอบของ 6

เลข 6 เป็นตัวประกอบของ 6 หรือไม่ ?

	ทดสอบโดยนำ 6 ไปหาร 6 ถ้าหารลงตัว แสดงว่า 6 เป็นตัวประกอบของ 6
	6 ÷ 6 หารลงตัว ได้ผลหารคือ 1 ดังนั้น 6 เป็นตัวประกอบของ 6
	6 ÷ 6 = 1 → 6 = 1 x 6

ตัวประกอบทั้งหมดของ 6 คือจำนวนนับทั้งหมดที่หาร 6 ลงตัว ได้แก้ 1, 2, 3, 6

ข้อสังเกต
ทุกจำนวนจะมี 1 และตัวมันเองเป็นตัวประกอบ
เพราะ 1 หารจำนวนใด ได้ผลหารคือจำนวนนั้น

ตัวอย่างที่ 1 ตัวประกอบของ 12 มีทั้งหมดกี่จำนวน ? จำนวนใดบ้าง ?

ถ้าใช้วิธีข้างต้น ต้องทดสอบตัวเลขตั้งแต่ 1 – 12 เพื่อหาว่ามีเลขจำนวนใดบ้างที่หาร 12 ลงตัว วิธีข้างต้น เป็นการคิดแบบตรงไปตรงมา เข้าใจง่าย แต่ไม่เหมาะกับเลขที่มีขนาดใหญ่ เพราะต้องใช้เวลามาก

วิธีที่จะแนะนำต่อไปนี้หาตัวประกอบทั้งหมดของ 12 ได้เร็วกว่าวิธีแรก แต่การคำนวณมีความซับซ้อนมากกว่า ในการทำข้อสอบ ขอแนะนำให้ใช้วิธีที่จะกล่าวต่อไปนี้ เพราะสามารถหาคำตอบได้ถูกต้อง ครบถ้วน โดยใช้เวลาไม่มาก