ตัวหารร่วมมาก และ ตัวคูณร่วมน้อย

ตัวประกอบร่วมของ 4, 8 และ 12 คือ
1, 2, 4 ซึ่งตัวที่มากที่สุดก็คือ 4
ห.ร.ม. คือ 4

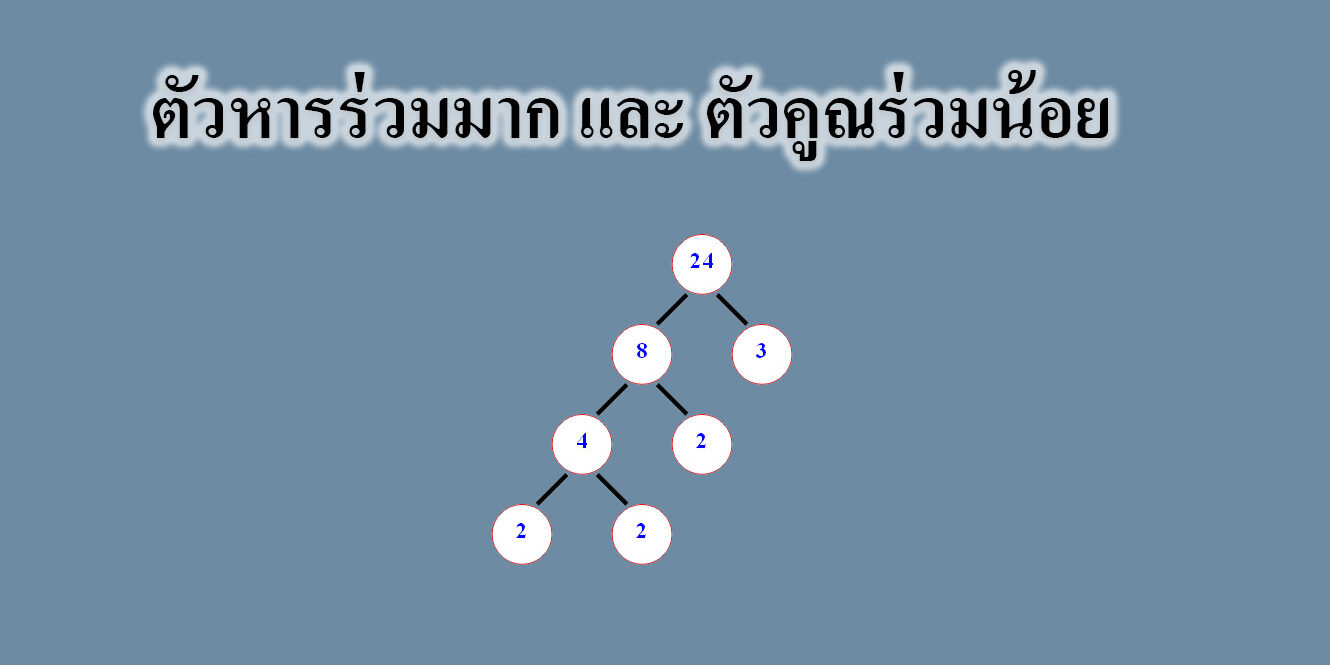
2. วิธีแยกตัวประกอบ 
4     = 2 x 2
8     = 2 x 2 x 2
12   = 2 x 2 x 3
เอาตัวที่ซ้ำมา

ห.ร.ม. คือ 2 x 2 = 4

3. วิธีตั้งหาร
2  ) 4    8    12
              2  ) 2    4      6
                     1    2      3

ห.ร.ม. คือ 2 x 2 = 4

4. วิธียุคลิด

พหุคูณร่วมของ 4, 8 และ 12 คือ
24, 48,……และมีต่อไปเรื่อยๆ ไม่รู้จบ
ซึ่งตัวที่น้อยที่สุดก็คือ 24
ค.ร.น. คือ 24

2. วิธีแยกตัวประกอบ  
4     = 2 x 2
8     = 2 x 2 x 2
12   = 2 x 2 x 3
เอาตัวที่ซ้ำหรือ ซ้ำแค่บางจำนวนและ จำนวนที่ไม่ซ้ำ
ค.ร.น คือ 2 x 2 x 2 x 3 = 24

3. วิธีตั้งหาร
              2  ) 4    8    12
              2  ) 2    4      6
                     1    2      3

           ค.ร.น คือ 2 x 2 x 2 x 3 = 24

(ในกรณี ค.ร.น. ตัวที่มาหาร ไม่จำเป็นต้องหารจำนวนทั้งหมดได้ ตัวที่ไม่ได้ถูกหารก็ให้คงค่าไว้)