ยูคลิด (Euclid) เป็นนักคณิตศาสตร์ชาวกรีก ซึ่งมีชีวิตอยู่ประมาณ 325 – 265 ปีก่อนคริสต์ศักราช ได้กล่าวถึงการหารร่วมมาก หรือ ห.ร.ม. ของจำนวนนับสองจำนวน ที่มีค่ามากได้อย่างรวดเร็วด้วยวิธีที่เรียกว่า ขั้นตอนวิธีแบบยูคลิด

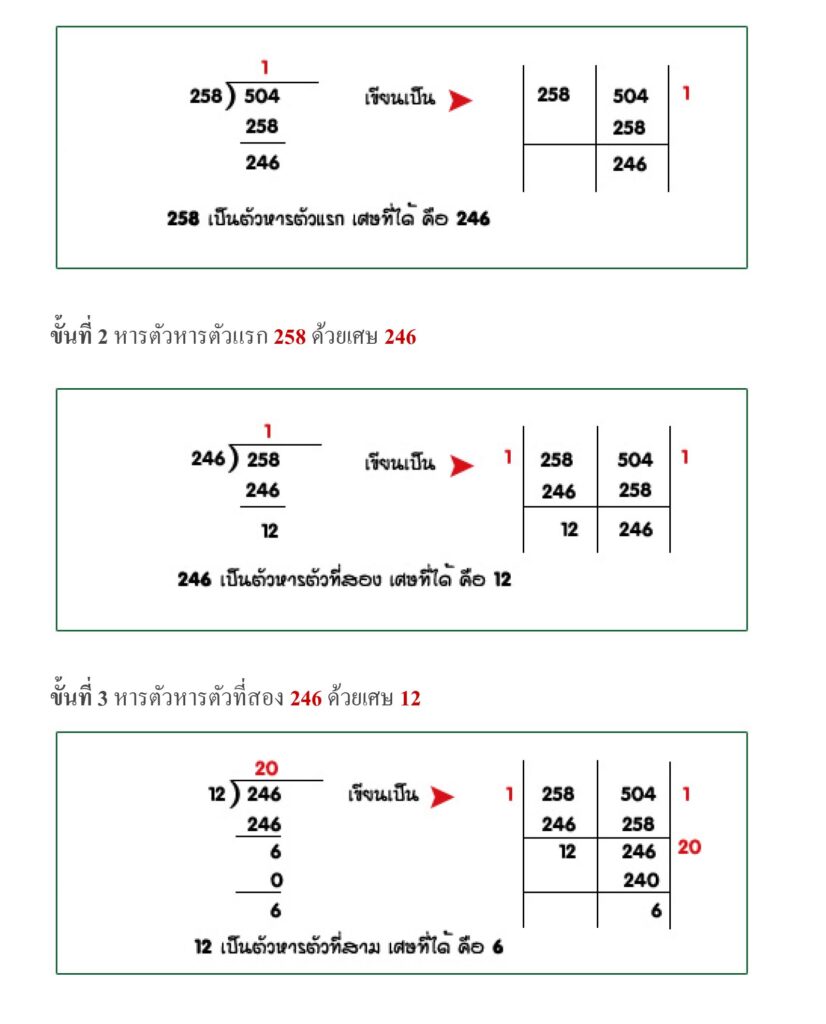
ขั้นที่ 4 หารตัวหารตัวที่สาม 12 ด้วย 6

การหารในครั้งนี้ลงตัว จึงยุติการหารและจะได้ตัวหารตัวสุดท้ายคือ 6 เป็น ห.ร.ม.ของ 258 และ 504
ดังนั้น ในทางปฏิบัติ การหา ห.ร.ม.ของจำนวนนับสองจำนวนตามวิธีการข้างต้น รวมทุกขั้นตอน เขียนได้ดังนี้
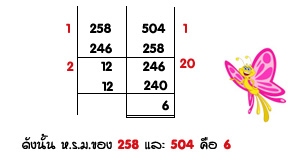
ตัวอย่าง การหา ห.ร.ม. โดยวิธีแบบยุคลิด
จงหา ห.ร.ม. ของ 231, 525 วิธีทำ 525 = 231*2 + 63 231 = 63*3 + 42 63 = 42*1 + 21 42 = 21*2 + 0 ห.ร.ม. ก็คือ 21 จงหา ห.ร.ม. ของ 68, 38 วิธีทำ 68 = 38*1 + 30 38 = 30*1 + 8 30 = 8*3 + 6 8 = 6*1 + 2 6 = 2*3 + 0 ห.ร.ม. ก็คือ 2 จงหา ห.ร.ม. ของ 56, 84, 140 gcd(56, 84, 140) = gcd(gcd(56, 84), 140) = gcd(56, gcd(84, 140)) วิธีทำ หา ห.ร.ม. ของ 56 กับ 84 ก่อน 84 = 56*1 + 28 56 = 28*2 + 0 ห.ร.ม. ของ 84 กับ 56 ก็คือ 28 ต่อไปหา ห.ร.ม. ของ 28 กับ 140 140 = 28*5 + 0 ห.ร.ม. ของ 140 กับ 28 ก็คือ 28 ดังนั้น ห.ร.ม. ก็คือ 28
การหา ห.ร.ม. ตามขั้นตอนวิธียุคลิด (Euclidean Algorithm)
4. การหา ห.ร.ม. ตามขั้นตอนวิธียุคลิด (Euclidean Algorithm)
ขั้นตอนที่ 1 นำจำนวนที่น้อยกว่าไปหารจำนวนมาก
ในที่นี้ 126 ÷ 45 = 2 เศษ 36
ขั้นตอนที่ 2 นำเศษที่เหลือในขั้นที่ 1 คือ 36 ไปหาร 45
จะได้ 45 ÷ 36 = 1 เศษ 9
ขั้นตอนที่ 3 นำเศษที่เหลือในขั้นตอนที่ 2 คือ 9 ไปหาร 36
จะได้ 36 ÷ 9 = 4 เศษ 0
ดังนั้น ห.ร.ม. คือ 9
สรุปหลักการ 1. เมื่อเศษเป็นศูนย์ แสดงว่าการหารจบสิ้นแล้ว
2. หารกลับไปกลับมาทางขวาและทางซ้าย
โดยนำตัวเศษหารต่อๆ ไปตัวหารตัวสุดท้าย
คือ ห.ร.ม. ในที่นี้คือ 9
ตัวอย่าง จงหา ห.ร.ม. ของ 348 และ 1,024 โดยวิธีตั้งหาร
ดังนั้น ห.ร.ม. ของ 348 และ 1,024 คือ 4
วิธีการหาร
1. นำจำนวนที่น้อยกว่าไปหารจำนวนที่มากกว่า ในที่นี้คือ 348 นำ 348 ไปหาร 1,024
ได้ 2 ใส่ผลลัพธ์ไว้ นำ 348 × 2 ได้ 696ไปลบออกจาก 1,024 คงเหลือ 348
2. นำ 328 ไปหาร 348 ได้ 1 ครั้ง 348 – 328 คงเหลือ 20
3. นำ 20 ไปหาร 328 ได้ 16 ครั้ง 328 – 320 คงเหลือ 8
4. นำ 8 ไปหาร 20 ได้ 2 ครั้ง 20 – 16 คงเหลือ 4
5. นำ 4 ไปหาร 8 ได้ 2 ครั้ง 8 – 8 คงเหลือ 0
6. จำนวนสุดท้าย คือ 4 ไปหาร 8 ได้ลงตัว เหลือเศษ 0 จำนวน 4 คือ ห.ร.ม.
ข้อควรสังเกต
การหา ห.ร.ม. โดยวิธีตั้งหารนี้จะใช้เมื่อจำนวนนับนั้นมีค่ามากๆ โดยนำมาตั้งทีละสองจำนวน ตั้งคู่กันไป นำจำนวนน้อยหารจำนวนมาก เมื่อลบกันแล้วนำผลลบไปหารอีกจำนวนหนึ่ง สลับกันไปจนกว่าจะหารได้ลงตัว เหลือเศษศูนย์ จำนวนที่เป็นตัวหารได้ลงตัวจำนวนสุดท้าย คือ ห.ร.ม.
1. การนำ ห.ร.ม. ไปประยุกต์ใช้กับการหาร
ห.ร.ม. ของ 15 และ 24 คือ 3
แต่ 15 = 16 – 1
16 = (x × 3) + 1
16 – 1 = x × 3
24 = 26 – 2
26 = (y × 3) + 2
26 – 2 = y × 3
จะเห็นว่า ถ้านำเศษมาลบออกจากตัวตั้ง ผลลัพธ์ที่ได้จะหารด้วย 3 ลงตัว
ตัวอย่างที่ 1 จงหาจำนวนที่มากที่สุดซึ่งหาร 212 และ 388 แล้วเหลือเศษ 2 และ 3 ตามลำดับ
วิธีทำ จำนวนที่นำไปหา ห.ร.ม. ได้ คือ
212 – 2 = 210
388 – 3 = 385
จำนวนที่มากที่สุด ซึ่งหาร 210 และ 385 ลงตัว คือ ห.ร.ม. ของสองจำนวนนั้น
1 210 385 1
175 210
35 175 5
175
0
ห.ร.ม. ของ 210 และ 385 คือ 35
ดังนั้น จำนวนที่มากที่สุดซึ่งหาร 212 และ 388 เหลือเศษ 2 และ 3 ตามลำดับ คือ 35
ตอบ 35
ตัวอย่างที่ 2 จงหาจำนวนที่มากที่สุด ซึ่งเมื่อนำไปหาร 856 และ 948 แล้วเหลือเศษ 5 เท่ากัน
วิธีทำ จำนวนที่นำไปหา ห.ร.ม. ได้ คือ
856 – 5 = 851
948 – 5 = 943
จำนวนที่มากที่สุดซึ่งหาร 851 และ 943 ลงตัว
ห.ร.ม. ของ 851 และ 943 คือ 23
ดังนั้น จำนวนที่มากที่สุดซึ่งหาร 851 และ 943 เหลือเศษ 5 เท่ากัน คือ 23
ตอบ 23
2. การนำ ห.ร.ม. ไปใช้กับการทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำ
ตัวอย่าง จงทอน ให้เป็นเศษส่วนอย่างต่ำ
ห.ร.ม. ของ 24 และ 42 คือ 6
เศษส่วนอย่างต่ำ คือ เศษส่วนที่มี ห.ร.ม. ของตัวเศษและตัวส่วนเป็น 1 เช่น , ,
3. การนำ ห.ร.ม. ไปใช้แก้โจทย์ปัญหา
ตัวอย่างที่ 1 มีเชือกอยู่สามเส้น ยาวเส้นละ 48, 60 และ 108 เมตร ถ้าตัดแบ่งให้ยาว เส้นละเท่าๆ กันให้ยาวที่สุดเท่าที่จะยาวได้ จะได้เชือกยาวเส้นละกี่เมตร และได้เชือกทั้งหมดกี่เส้น
วิธีทำ 48 = 2 × 2 × 2 × 2 × 3
60 = 2 × 2 × 3 × 5
108 = 2 × 2 × 2 × 3 × 3 × 3
ห.ร.ม. คือ 2 × 2 × 3 หรือ 12
ดังนั้น จะแบ่งเชือกได้ยาวที่สุดเส้นละ 12 เมตร
เชือกเส้นแรกแบ่งได้ = 4 เส้น
เชือกเส้นสองแบ่งได้ = 5 เส้น
เชือกเส้นสามแบ่งได้ = 9 เส้น
ดังนั้น จะได้เชือกทั้งหมด 4 + 5 + 9 = 18 เมตร
ตอบ จะได้เชือกยาวเส้นละ 12 เมตร และได้เชือกยาวทั้งหมด 18 เส้น
ตัวอย่างที่ 2 ไม้อัดรูปสี่เหลี่ยมผืนผ้ากว้าง 1.20 เมตร ยาว 2.40 เมตร ต้องการตัดไม้อัดนี้ให้เป็นรูปสี่เหลี่ยมจัตุรัสให้มีพื้นที่มากที่สุดจะได้ไม้อัดรูปสี่เหลี่ยมจัตุรัสยาวด้านละเท่าไรและได้ไม้อัดรูปสี่เหลี่ยมจัตุรัสกี่แผ่น
วิธีทำ ไม้อัดรูปสี่เหลี่ยมผืนผ้ากว้าง 1.20 เมตร ยาว 2.40 เมตร ต้องการตัดไม้อัดนี้ ให้เป็นรูปสี่เหลี่ยมจัตุรัสให้มีพื้นที่มากที่สุด
ดังนั้น ต้องการหาความยาวที่ยาวที่สุดของด้านของรูปสี่เหลี่ยมจัตุรัส คือ ห.ร.ม. ของ 1.20 เมตร และ 2.40 เมตร
ไม้อัดกว้าง 1.20 เมตร หรือ 120 เซนติเมตร
ไม้อัดยาว 2.40 เมตร หรือ 240 เซนติเมตร
120 = 2 × 2 × 2 × 3 × 5
240 = 2 × 2 × 2 × 2 × 3 × 5
ห.ร.ม. คือ 2 × 2× 2 × 3 × 5 หรือ 120
ไม้อัดด้านกว้างแบ่งได้ = 1 ส่วน
ไม้อัดด้านยาวแบ่งได้ = 2 ส่วน
ได้ไม้อัดรูปสี่เหลี่ยมจัตุรัส 1 × 2 = 2 แผ่น






