ทฤษฎีจำนวน-การหารลงตัวและขั้นตอนวิธีการหาร

ทฤษฎีจำนวน-การหารลงตัวและขั้นตอนวิธีการหาร

• การหารลงตัว
	บทนิยาม	กำหนด a, b เป็นจำนวนเต็มใดๆ โดยที่ b ≠ 0  b หาร a ลงตัว ก็ต่อเมื่อ มีจำนวนเต็ม n ที่ทำให้ a = bn  และเขียนแทน “b หาร a ลงตัว” ได้ด้วยสัญลักษณ์ b | a
จากบทนิยาม ถ้า b หาร a ไม่ลงตัว แสดงว่าไม่มีจำนวนเต็ม n ที่ทำให้ a = bn และ เขียนแทน “b หาร a ไม่ลงตัว” ได้ด้วยสัญลักษณ์ b † a
	ตัวอย่างเช่น	3 | 9 เพราะมี n = 3 ที่ทำให้  9 = 3n
		-5 | 10 เพราะมี n = -2 ที่ทำให้ 10 = +5n
		6 | 0 เพราะมี n = 0 ที่ทำให้ 0 = 6n
สมบัติการหารลงตัว
	ทฤษฎีบทที่ 1	กำหนด a, b, c เป็นจำนวนเต็มใดๆ ถ้า a | b และ b | c แล้วจะได้ a | c
	ทฤษฎีบทที่ 2	กำหนด a, b เป็นจำนวนเต็มบวก ถ้า a | b แล้วจะได้ a ≤ b
	ทฤษฎีบทที่ 3	กำหนด a, b, c เป็นจำนวนเต็มใดๆ ถ้า a | b และ b | c แล้วจะได้ a | bx + cy เมื่อ x, y เป็นจำนวนเต็มใดๆ
การจำแนกจำนวนเต็มบวกโดยใช้สมบัติการหารลงตัว
1.จำนวนเฉพาะ (Prime Numbers)
	บทนิยาม	จำนวนเต็ม  p จะเป็นจำนวนเฉพาะ ก็ต่อเมื่อ p ≠ 0, p ≠ 1, p ≠ -1 และถ้ามีจำนวนเต็มที่หาร p ลงตัว จำนวนเต็มนั้นต้องเป็นสมาชิกของ {-1, 1, p, -p}
2.จำนวนประกอบ (Composite Numbers)
	บทนิยาม	จำนวนเต็ม c เป็นจำนวนเต็มบวกที่มากกว่า 1 จะเป็นจำนวนประกอบ ก็ต่อเมื่อ c ไม่ใช่จำนวนเฉพาะ
	นั่นคือสำหรับจำนวนเต็มบวก c ใดๆ c จะเป็นจำนวนประกอบ ก็ต่อเมื่อ มีจำนวนเต็ม m และ n ที่ต่างจาก c ที่ทำให้ c = mn
	ตัวอย่างเช่น
	จำนวนที่หาร 2 ลงตัว ได้แก่ {-1, 1, 2, -2} ∴ 2 เป็นจำนวนเฉพาะ        จำนวนที่หาร 3 ลงตัว ได้แก่ {-1, 1, 3, -3} ∴ 3 เป็นจำนวนเฉพาะ        จำนวนที่หาร 4 ลงตัว ได้แก่ {-4, -2, -1, 1, 2, 4} ∴ 4 ไม่เป็นจำนวนเฉพาะ
• ขั้นตอนวิธีการหาร
	ถ้า a และ b เป็นจำนวนเต็ม โดยที่ b ≠ 0 แล้วจะมี q และ r ซึ่งเป็นจำนวนเต็มที่ทำให้                      a = bq + r เมื่อ 0 r |b| นั่นคือ a เป็นตัวตั้งหารด้วย b ได้ผลหารคือ q และเศษ r
	ตัวอย่างที่ 1	กำหนด a = 48, b = 7 จงหา q และ r
		เขียนให้อยู่ในรูป	a = bq + r
			48 = 7 × 6 +6
		∴	q = 6 และ r = 6
• ตัวหารร่วม
	ตัวหารร่วม
	กำหนด a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์ เรียกจำนวนเต็ม c       ซึ่ง c | a และ c | b ว่าเป็น “ตัวหารร่วม” ของ a และ b
	ตัวหารร่วมมาก
	กำหนด a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์พร้อมกัน เรียกจำนวนเต็มบวก d ที่มีค่ามากที่สุด ซึ่ง d | a และ d | b ว่าเป็น “ตัวหารร่วมมาก” (ห.ร.ม.) ของ a และ b เขียนแทนด้วยสัญลักษณ์ (a, b)
	ตัวอย่างเช่น	จงหา ห.ร.ม. ของ 36 และ 48
	วิธีทำ	ตัวหารร่วมของ 36 ได้แก่ ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ±36
		ตัวหารร่วมของ 48 ได้แก่ ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±16, ±24, ±48
	∴	ตัวหารร่วมที่เป็นบวกของ 36 และ 48 ได้แก่ 1, 2, 3, 4, 6, 12
	∴	ตัวหารร่วมที่เป็นบวกของ 36 และ 48 ที่มีค่ามากที่สุด คือ12
		นั่นคือ ห.ร.ม. ของ 36 และ 48 คือ 12

การหาตัวหารร่วมมากโดยใช้ขั้นตอนวิธีของยุคลิด

การหา ห.ร.ม. ตามขั้นตอนวิธียุคลิด (Euclidean Algorithm)

4. การหา ห.ร.ม. ตามขั้นตอนวิธียุคลิด (Euclidean Algorithm)

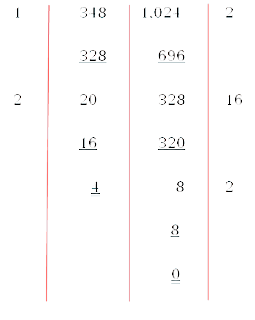
ขั้นตอนที่ 1 นำจำนวนที่น้อยกว่าไปหารจำนวนมาก           

        ในที่นี้ 126 ÷ 45 = 2 เศษ 36

ขั้นตอนที่ 2 นำเศษที่เหลือในขั้นที่ 1 คือ 36 ไปหาร 45

                 จะได้ 45 ÷ 36 = 1 เศษ 9

ขั้นตอนที่ 3 นำเศษที่เหลือในขั้นตอนที่ 2 คือ 9 ไปหาร 36

                 จะได้ 36 ÷ 9 = 4 เศษ 0

       ดังนั้น ห.ร.ม. คือ 9

สรุปหลักการ             1. เมื่อเศษเป็นศูนย์ แสดงว่าการหารจบสิ้นแล้ว

            2. หารกลับไปกลับมาทางขวาและทางซ้าย

โดยนำตัวเศษหารต่อๆ ไปตัวหารตัวสุดท้าย    

คือ ห.ร.ม. ในที่นี้คือ 9

 

ตัวอย่าง จงหา ห.ร.ม. ของ 348 และ 1,024 โดยวิธีตั้งหาร

                     

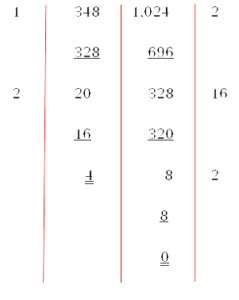
ดังนั้น ห.ร.ม. ของ 348 และ 1,024 คือ 4

วิธีการหาร

1. นำจำนวนที่น้อยกว่าไปหารจำนวนที่มากกว่า ในที่นี้คือ 348 นำ 348 ไปหาร 1,024

   ได้ 2 ใส่ผลลัพธ์ไว้ นำ 348 × 2 ได้ 696ไปลบออกจาก 1,024 คงเหลือ 348

2. นำ 328 ไปหาร 348 ได้ 1 ครั้ง 348 – 328 คงเหลือ 20

3. นำ 20 ไปหาร 328 ได้ 16 ครั้ง 328 – 320 คงเหลือ 8

4. นำ 8 ไปหาร 20 ได้ 2 ครั้ง 20 – 16 คงเหลือ 4

5. นำ 4 ไปหาร 8 ได้ 2 ครั้ง 8 – 8 คงเหลือ 0

6. จำนวนสุดท้าย คือ 4 ไปหาร 8 ได้ลงตัว เหลือเศษ 0 จำนวน 4 คือ ห.ร.ม.

 

ข้อควรสังเกต    

การหา ห.ร.ม. โดยวิธีตั้งหารนี้จะใช้เมื่อจำนวนนับนั้นมีค่ามากๆ โดยนำมาตั้งทีละสองจำนวน ตั้งคู่กันไป นำจำนวนน้อยหารจำนวนมาก

เมื่อลบกันแล้วนำผลลบไปหารอีกจำนวนหนึ่ง สลับกันไปจนกว่าจะหารได้ลงตัว เหลือเศษศูนย์ จำนวนที่เป็นตัวหารได้ลงตัวจำนวนสุดท้าย คือ ห.ร.ม.

จำนวนเฉพาะสัมพัทธ์
	บทนิยาม	จำนวนเต็ม a และ b จะเป็นจำนวนเฉพาะสัมพัทธ์กันก็ต่อเมื่อ (a, b) = 1
• ตัวคูณร่วมน้อย
	ตัวคูณร่วมน้อย
	กำหนด a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์ เรียกจำนวนเต็มบวก c ที่มีค่าน้อยที่สุด ซึ่ง a | c และ b | c ว่าเป็น “ตัวคูณร่วมน้อย” (ค.ร.น.) ของ a และ b เขียนแทนด้วยสัญลักษณ์ [a, b]
	ตัวอย่างเช่น	จงหา ค.ร.น. ของ 36 และ 24
	วิธีทำ	พหุคูณที่เป็นบวกของ 36 ได้แก่ 36, 72, 108, 144, …
	∴	พหุคูณที่เป็นบวกของ 24 ได้แก่ 24, 48, 72, 96, 120, 144, …
	∴	พหุคูณร่วมที่เป็นบวกของ 36 และ 24 ได้แก่ 72, 144, …
		พหุคูณร่วมที่เป็นบวกของ 36 และ 24 ที่มีค่าน้อยที่สุด คือ 72
		นั่นคือ ค.ร.น. ของ 36 และ 24 คือ 72