ทฤษฎีจำนวน (NUMBER THEORY) คณิตศาสตร์ ม.ปลาย

เรียนเลข ทฤษฎีจำนวน (NUMBER THEORY)

หนังสือ โลกทฤษฎีจำนวน เล่มนี้เหมาะสมสำหรับการเรียนการสอนวิชา ทฤษฎีจำนวน ในระดับปริญญาตรีและนักเรียนที่ต้องการเป็นตัวแทนประเทศไทยเพื่อเข้าสอบคณิตศาสตร์โอลิมปิกระหว่างประเทศ (IMO) ภายในเล่มได้รวบรวมเนื้อหาที่สำคัญเช่น – หลักอุปนัยเชิงคณิตศาสตร์ – การหารลงตัว ขั้นตอนวิธการหารของยุคลิด – ตัวหารร่วมมาก ตัวคูณร่วมน้อย จำนวนเฉพาะ – ทฤษฎีบทหลักมูลของเลขคณิต – ลงรอย ผลเฉลยของสมการลงรอย – ฟังก์ชันเลขคณิต ฟังก์ชันแยกคูณ – ฟังก์ชันพื้น ฟังก์ชันเพดาน ฟังก์ชันเลอจองด์ – สมการไดโอแฟนไทน์เชิงเส้น – ทฤษฎีบทเศษเหลือของจีน – Gauss’s theorem Fermat’s theorem – Euler’s theorem Fermat’s theorem – Fermat’s Little theorem รากปฐมฐาน – จำนวนแฟร์มาต์ จำนวนแมร์เซน จำนวนสมบูรณ์ – จำนวนฟิโบนักชี จำนวนสามเหลี่ยม

“จำนวนเฉพาะ” หรือ ไพรม์ นัมเบอร์ (Prime number) คือ จำนวนธรรมชาติที่มีตัวหารที่เป็นบวกอยู่ 2 ตัว คือ 1 กับตัวมันเอง เช่น 2, 3, 5, 7, 11, 13 และ 17 เป็นต้น และสำหรับเลข 1 นั้น ให้ตัดทิ้ง เพราะ 1 ไม่เป็นจำนวนเฉพาะ จำนวนเฉพาะ เป็น จำนวนที่มีตัวประกอบเป็นจำนวนเต็มเพียงสองจำนวนเท่านั้น ที่สามารถนำมาหารจำนวนเฉพาะนี้แล้วลงตัว ซึ่งจำนวนเต็มอื่น ๆ จะไม่สามารถนำมาหารจำนวนเฉพาะได้ลงตัวเลย ยกเว้น 1 ซึ่งเป็นเอกลักษณ์ของการคูณและตัวมันเอง ยกตัวอย่างเช่น 7 เป็นจำนวนเฉพาะ เนื่องมีตัวประกอบ คือ 1 และ 7 และไม่มีจำนวนอื่น ๆ ที่นำมาหาร 7 แล้วลงตัว ในขณะที่ 6 ไม่ใช่จำนวนเฉพาะ เนื่องจาก นอกจาก 1 และ 6 แล้วยังมีจำนวนเต็มอื่น ๆ คือ 2 และ 3 ที่สามารถนำมาหาร 6 ได้ลงตัว หลาย ๆ คนที่เริ่มพิจารณาว่าจำนวนเต็มใดเป็นจำนวนเฉพาะ มักจะเข้าใจผิดว่าจำนวนคู่ทุกจำนวนไม่เป็นจำนวนเฉพาะ เนื่องจากจำนวนคู่มีนิยามคือ จำนวนที่หารด้วย 2 แล้วลงตัวหรือมีเศษเหลือเป็นศูนย์ แต่มีข้อยกเว้นบางจำนวน นั่นคือ 2 เป็นจำนวนคู่เพียงจำนวนเดียวที่เป็นจำนวนเฉพาะ เนื่องจาก 2 มีตัวประกอบคือ 1 และ 2 เท่านั้น ไม่มีจำนวนอื่นใดที่สามารถนำมาหาร 2 แล้วลงตัว ตัวอย่างจำนวนเฉพาะที่เรานำมาฝาก มีดังนี้ จํานวนเฉพาะ 1-100 มีทั้งหมด 25 ตัว ดังนี้ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 และ 97 จํานวนเฉพาะ 1-200 มีทั้งหมด 46 ตัว ดังนี้ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197 และ 199

• การหารลงตัว
	บทนิยาม	กำหนด a, b เป็นจำนวนเต็มใดๆ โดยที่ b ≠ 0 b หาร a ลงตัว ก็ต่อเมื่อ มีจำนวนเต็ม n ที่ทำให้ a = bn และเขียนแทน “b หาร a ลงตัว” ได้ด้วยสัญลักษณ์ b | a
จากบทนิยาม ถ้า b หาร a ไม่ลงตัว แสดงว่าไม่มีจำนวนเต็ม n ที่ทำให้ a = bn และ เขียนแทน “b หาร a ไม่ลงตัว” ได้ด้วยสัญลักษณ์ b † a
	ตัวอย่างเช่น	3 | 9 เพราะมี n = 3 ที่ทำให้  9 = 3n
		-5 | 10 เพราะมี n = -2 ที่ทำให้ 10 = +5n
		6 | 0 เพราะมี n = 0 ที่ทำให้ 0 = 6n
สมบัติการหารลงตัว
	ทฤษฎีบทที่ 1	กำหนด a, b, c เป็นจำนวนเต็มใดๆ ถ้า a | b และ b | c แล้วจะได้ a | c
	ทฤษฎีบทที่ 2	กำหนด a, b เป็นจำนวนเต็มบวก ถ้า a | b แล้วจะได้ a ≤ b
	ทฤษฎีบทที่ 3	กำหนด a, b, c เป็นจำนวนเต็มใดๆ ถ้า a | b และ b | c แล้วจะได้ a | bx + cy เมื่อ x, y เป็นจำนวนเต็มใดๆ
การจำแนกจำนวนเต็มบวกโดยใช้สมบัติการหารลงตัว
1.จำนวนเฉพาะ (Prime Numbers)
	บทนิยาม	จำนวนเต็ม  p จะเป็นจำนวนเฉพาะ ก็ต่อเมื่อ p ≠ 0, p ≠ 1, p ≠ -1 และถ้ามีจำนวนเต็มที่หาร p ลงตัว จำนวนเต็มนั้นต้องเป็นสมาชิกของ {-1, 1, p, -p}
2.จำนวนประกอบ (Composite Numbers)
	บทนิยาม	จำนวนเต็ม c เป็นจำนวนเต็มบวกที่มากกว่า 1 จะเป็นจำนวนประกอบ ก็ต่อเมื่อ c ไม่ใช่จำนวนเฉพาะ
	นั่นคือสำหรับจำนวนเต็มบวก c ใดๆ c จะเป็นจำนวนประกอบ ก็ต่อเมื่อ มีจำนวนเต็ม m และ n ที่ต่างจาก c ที่ทำให้ c = mn
	ตัวอย่างเช่น
	จำนวนที่หาร 2 ลงตัว ได้แก่ {-1, 1, 2, -2} ∴ 2 เป็นจำนวนเฉพาะ จำนวนที่หาร 3 ลงตัว ได้แก่ {-1, 1, 3, -3} ∴ 3 เป็นจำนวนเฉพาะ จำนวนที่หาร 4 ลงตัว ได้แก่ {-4, -2, -1, 1, 2, 4} ∴ 4 ไม่เป็นจำนวนเฉพาะ
• ขั้นตอนวิธีการหาร
	ถ้า a และ b เป็นจำนวนเต็ม โดยที่ b ≠ 0 แล้วจะมี q และ r ซึ่งเป็นจำนวนเต็มที่ทำให้ a = bq + r เมื่อ 0 r |b| นั่นคือ a เป็นตัวตั้งหารด้วย b ได้ผลหารคือ q และเศษ r
	ตัวอย่างที่ 1	กำหนด a = 48, b = 7 จงหา q และ r
		เขียนให้อยู่ในรูป	a = bq + r
			48 = 7 × 6 +6
		∴	q = 6 และ r = 6
• ตัวหารร่วม
	ตัวหารร่วม
	กำหนด a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์ เรียกจำนวนเต็ม c ซึ่ง c | a และ c | b ว่าเป็น “ตัวหารร่วม” ของ a และ b
	ตัวหารร่วมมาก
	กำหนด a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์พร้อมกัน เรียกจำนวนเต็มบวก d ที่มีค่ามากที่สุด ซึ่ง d | a และ d | b ว่าเป็น “ตัวหารร่วมมาก” (ห.ร.ม.) ของ a และ b เขียนแทนด้วยสัญลักษณ์ (a, b)
	ตัวอย่างเช่น	จงหา ห.ร.ม. ของ 36 และ 48
	วิธีทำ	ตัวหารร่วมของ 36 ได้แก่ ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ±36
		ตัวหารร่วมของ 48 ได้แก่ ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±16, ±24, ±48
	∴	ตัวหารร่วมที่เป็นบวกของ 36 และ 48 ได้แก่ 1, 2, 3, 4, 6, 12
	∴	ตัวหารร่วมที่เป็นบวกของ 36 และ 48 ที่มีค่ามากที่สุด คือ12
		นั่นคือ ห.ร.ม. ของ 36 และ 48 คือ 12

การหาตัวหารร่วมมากโดยใช้ขั้นตอนวิธีของยุคลิด

การหา ห.ร.ม. ตามขั้นตอนวิธียุคลิด (Euclidean Algorithm)

4. การหา ห.ร.ม. ตามขั้นตอนวิธียุคลิด (Euclidean Algorithm)

ขั้นตอนที่ 1 นำจำนวนที่น้อยกว่าไปหารจำนวนมาก

ในที่นี้ 126 ÷ 45 = 2 เศษ 36

ขั้นตอนที่ 2 นำเศษที่เหลือในขั้นที่ 1 คือ 36 ไปหาร 45

จะได้ 45 ÷ 36 = 1 เศษ 9

ขั้นตอนที่ 3 นำเศษที่เหลือในขั้นตอนที่ 2 คือ 9 ไปหาร 36

จะได้ 36 ÷ 9 = 4 เศษ 0

ดังนั้น ห.ร.ม. คือ 9

สรุปหลักการ             1. เมื่อเศษเป็นศูนย์ แสดงว่าการหารจบสิ้นแล้ว

2. หารกลับไปกลับมาทางขวาและทางซ้าย

โดยนำตัวเศษหารต่อๆ ไปตัวหารตัวสุดท้าย

คือ ห.ร.ม. ในที่นี้คือ 9

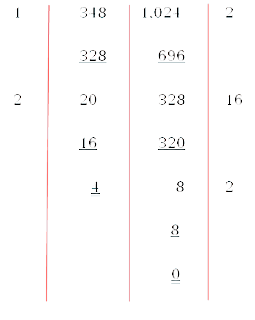
ตัวอย่าง จงหา ห.ร.ม. ของ 348 และ 1,024 โดยวิธีตั้งหาร

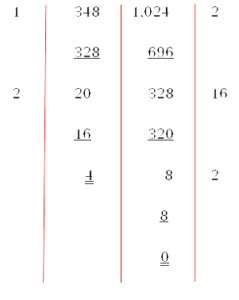
ดังนั้น ห.ร.ม. ของ 348 และ 1,024 คือ 4

วิธีการหาร

1. นำจำนวนที่น้อยกว่าไปหารจำนวนที่มากกว่า ในที่นี้คือ 348 นำ 348 ไปหาร 1,024

ได้ 2 ใส่ผลลัพธ์ไว้ นำ 348 × 2 ได้ 696ไปลบออกจาก 1,024 คงเหลือ 348

2. นำ 328 ไปหาร 348 ได้ 1 ครั้ง 348 – 328 คงเหลือ 20

3. นำ 20 ไปหาร 328 ได้ 16 ครั้ง 328 – 320 คงเหลือ 8

4. นำ 8 ไปหาร 20 ได้ 2 ครั้ง 20 – 16 คงเหลือ 4

5. นำ 4 ไปหาร 8 ได้ 2 ครั้ง 8 – 8 คงเหลือ 0

6. จำนวนสุดท้าย คือ 4 ไปหาร 8 ได้ลงตัว เหลือเศษ 0 จำนวน 4 คือ ห.ร.ม.

ข้อควรสังเกต

การหา ห.ร.ม. โดยวิธีตั้งหารนี้จะใช้เมื่อจำนวนนับนั้นมีค่ามากๆ โดยนำมาตั้งทีละสองจำนวน ตั้งคู่กันไป นำจำนวนน้อยหารจำนวนมาก

เมื่อลบกันแล้วนำผลลบไปหารอีกจำนวนหนึ่ง สลับกันไปจนกว่าจะหารได้ลงตัว เหลือเศษศูนย์ จำนวนที่เป็นตัวหารได้ลงตัวจำนวนสุดท้าย คือ ห.ร.ม.

จำนวนเฉพาะสัมพัทธ์
	บทนิยาม	จำนวนเต็ม a และ b จะเป็นจำนวนเฉพาะสัมพัทธ์กันก็ต่อเมื่อ (a, b) = 1
• ตัวคูณร่วมน้อย
	ตัวคูณร่วมน้อย
	กำหนด a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์ เรียกจำนวนเต็มบวก c ที่มีค่าน้อยที่สุด ซึ่ง a | c และ b | c ว่าเป็น “ตัวคูณร่วมน้อย” (ค.ร.น.) ของ a และ b เขียนแทนด้วยสัญลักษณ์ [a, b]
	ตัวอย่างเช่น	จงหา ค.ร.น. ของ 36 และ 24
	วิธีทำ	พหุคูณที่เป็นบวกของ 36 ได้แก่ 36, 72, 108, 144, …
	∴	พหุคูณที่เป็นบวกของ 24 ได้แก่ 24, 48, 72, 96, 120, 144, …
	∴	พหุคูณร่วมที่เป็นบวกของ 36 และ 24 ได้แก่ 72, 144, …
		พหุคูณร่วมที่เป็นบวกของ 36 และ 24 ที่มีค่าน้อยที่สุด คือ 72
		นั่นคือ ค.ร.น. ของ 36 และ 24 คือ 72

คอนกรูเอนซ์ (Congruence)

• a คอนกรูเอนซ์(congruent) กับ b มอดุโล m, เขียนได้ว่า “aคอนกรูเอนซ์b (mod m)”, ก็ต่อเมื่อ m | a-b เรียก m ว่า มอดุลัส
•หรือเขียนได้ว่า: (a-b) mod m = 0
ข้อสังเกตุ
1. a คอนกรูเอนซ์ b (mod m) ก็ต่อเมื่อ a mod m = b mod m
2. a คอนกรูเอนซ์ b (mod m) ก็ต่อเมื่อมีจำนวนเต็ม k ซึ่งทำให้ a= b+km

ตัวตั้ง = (ผลหาร × ตัวหาร) + เศษ