ทฤษฎีบททวินาม
ในหัวข้อนี้จะกล่าวถึงสูตรของการกระจาย ( x + y )2 เมื่อ x, y เป็นจำนวนจริงใดๆ และ n เป็นจำนวนเต็มบวก พิจารณาการกระจายต่อไปนี้
( x + y )1 = x + y
(x + y )2 = x2 + 2xy + y2
( x + y )3 = x3 +3x2 y + 3xy2 y3
( x + y )4 = x4 + 4x3 y + 6x2 y2 + 4xy3 + y4
(x + y )5 = x5 + 5x4 y + 10x3 y2 + 10x2 y3 +5xy4 + y5
พิจารณา (x + y )n = (x + y)(x + y)… ( x + y ) = n วงเล็บ
ในการกระจายเลือก x และ y อย่างใดอย่างหนึ่งของแต่ละวงเล็บนำมาคูณกันแล้วนำผลคูณ
ที่ได้มาบวกกัน เช่นเลือก y จาก 2 วงเล็บ และเลือก x จาก n – 2 วงเล็บที่เหลือจะได้พจน์ xn – 2 y2 ดังนั้น แต่ละพจน์ของการกระจาย ( x + y )n อยู่ในรูป xn – r yr เมื่อ r {0,1,2,…, n}
เนื่องจาก xn – r yr ประกอบด้วย x จำนวน n – r ตัว และ y จำนวน r ตัว ดังนั้น พจน์ xn – r yr มีทั้งหมด
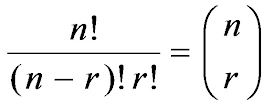
พจน์
นั่นคือ สัมประสิทธิ์ของ xn – r yr เท่ากับ
การกระจาย ( x + y )n สรุปเป็นทฤษฏีบทได้ดังนี้



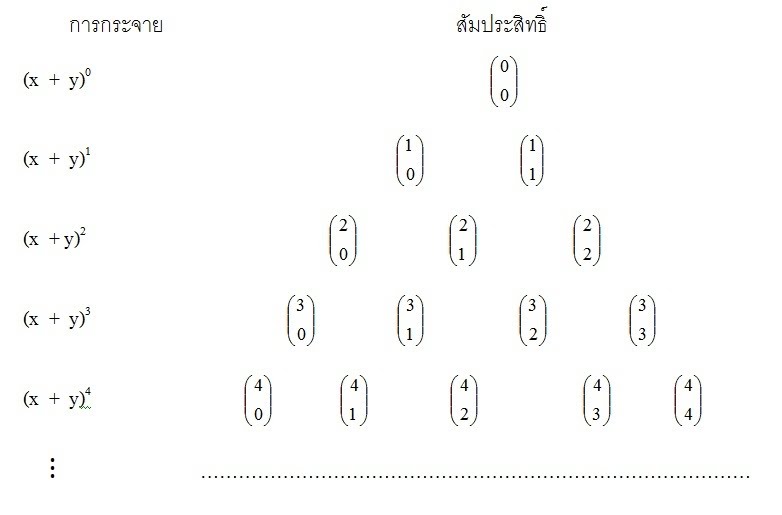


ของรูปสามเหลี่ยมปาสกาล ซึ่งจะได้ว่า
( x + y )4 = x4 + 4x3 y + 6x2 y2 + 4xy3 + y4







