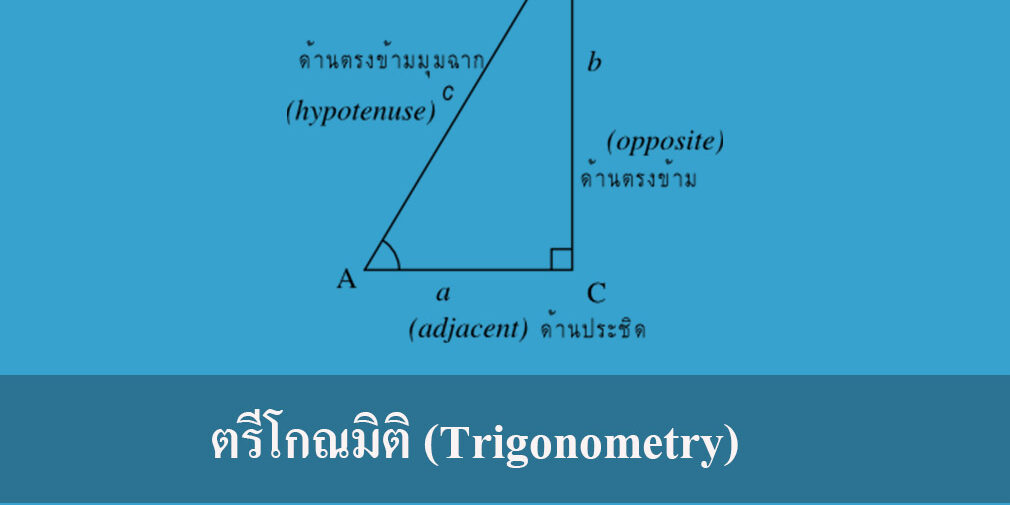
- กล่าวว่าสามเหลี่ยมใด ๆ จะเป็นสามเหลี่ยมมุมฉากก็ต่อเมื่อ ก าลังสองของด้านที่ยาวที่สุดจะเท่ากับผลรวมของก าลัง
- สองของอีกสองด้านที่เหลือ
- เช่ น ก าหนดความยาวของด้านทั้ง 3 ของรูปสามเหลี่ยมเป็น 3,4,5 หน่วย ตามล าดับ
- ตามทฤษฎีบทกลับจะได้ว่า 5
- 2= 4
- 2+3
- 25 =16+9
- 25 = 25
บทกลับของทฤษฎีบทปีทาโกรัส โดยกล่าวไว้ดังนี้
“กำหนด a, b และ c เป็นจำนวนจริงบวกที่ a2 + b2 = c2 จะมีสามเหลื่ยมมุมฉากหนึ่งรูปที่มีความยาวด้าน เป็น จำนวนสามจำนวนนั้น และด้านที่มีความยาว a และ b จะเป็นด้านประกอบมุมฉากของรูปสามเหลื่ยมนั้น”
บทกลับนี้ยังปรากฏอยู่ในหนังสือ Euclid’s Elements ของ ยุคลิดด้วย โดยบทกลับนี้สามารถพิสูจน์ได้โดยใช้ กฎของโคไซน์ หรือตามการพิสูจน์ดังต่อไปนี้
“กำหนดสามเหลี่ยม ABC มีด้านสามด้านที่มีความยาว a,b และ c และ a2 + b2 = c2 เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ “ด้าน-ด้าน-ด้าน” และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย”
จากบทพิสูจน์ของบทกลับของทฤษฎีบทปีทาโกรัส เราสามารถนำไปหาว่ารูปสามเหลี่ยมใด ๆ เป็นสามเหลี่ยมมุมแหลม, มุมฉาก หรือ มุมป้าน ได้ เมื่อกำหนดให้ c เป็นความยาวของด้านที่ยาวที่สุดในรูปสามเหลี่ยม
ถ้า a2 + b2 = c2 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก
ถ้า a2 + b2 < c2 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม
ถ้า a2 + b2 > c2 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน
ดังนั้น สามเหลี่ยมดังกล่าวจึงเป็นสามเหลี่ยมมุมฉาก
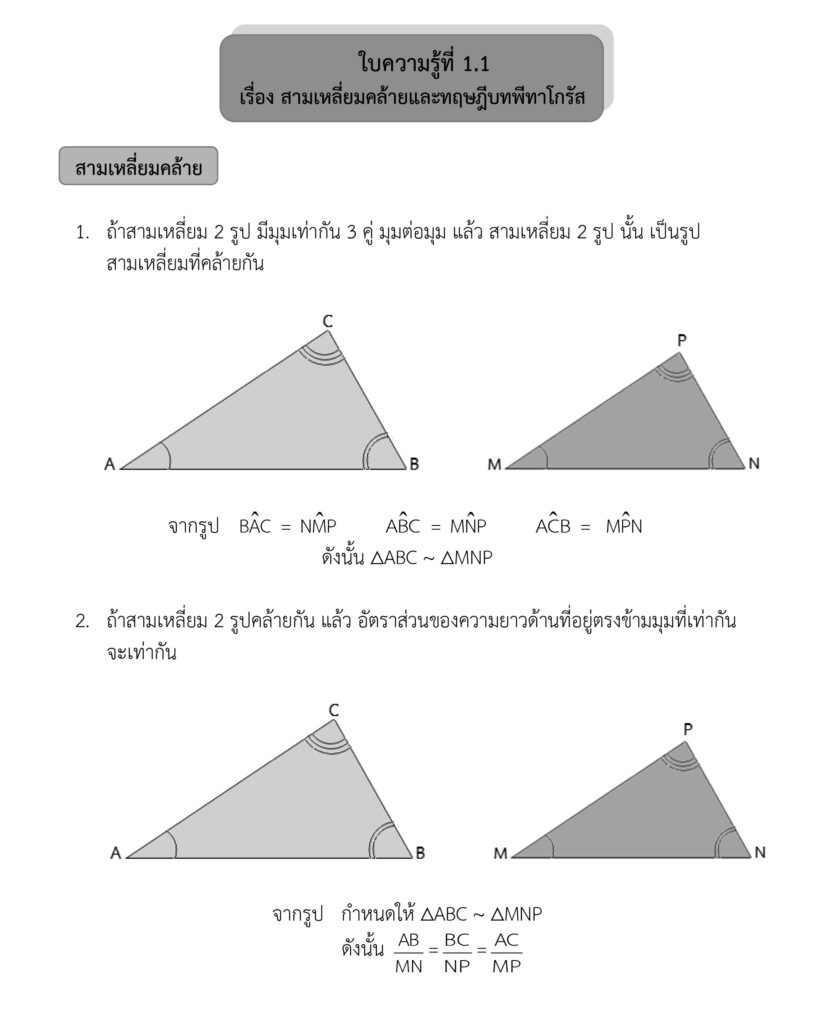
สามเหลี่ยมคล้าย
- คือ สามเหลี่ยมสองรูปที่ขนาดของมุมเท่ากันทั้งสามคู่
- สัญลักษณ์ที่ใช้คือ ~ แทนค าว่า “คล้ายกับ”