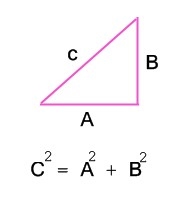ทฤษฎีบทพีทาโกรัส-คณิตศาสตร์ ม.ต้น

ทฤษฎีบทพีทาโกรัส

คณิตศาสตร์นี้ฟรีทันทีจะแก้สมการพีทาโกรัสทฤษฎีบทพีทาโกรัสว่า a²+b²=c² และสามารถใช้ในการค้นหาความยาวของด้านตรงข้ามมุมฉากของรูปสามเหลี่ยมขวา ที่จะคำนวณด้านที่สามตามทฤษฎีบทพีทาโกรัส
ตัวอย่างเช่นป้อนด้านข้างและด้านข้าง B และเครื่องคิดเลขจะคำนวณความยาวของด้าน C

ถ้า a, b เป็นความยาวด้านประกอบมุมฉาก

ของรูปสามเหลี่ยมมุมฉาก

c เป็นความยาวด้านตรงข้ามมุมฉาก

ของรูปสามเหลี่ยมมุมฉาก

จะได้ว่า c² = a² + b²

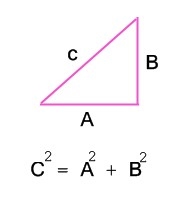
$ในวิชาคณิตศาสตร์ ทฤษฎีบทพีทาโกรัส แสดงความสัมพันธ์ในเรขาคณิตแบบยุคลิด ระหว่างด้านทั้งสามของสามเหลี่ยมมุมฉาก กำลังสองของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของอีกสองด้านที่เหลือ ในเรื่องของพื้นที่ได้กล่าวไว้ดังนี้ " ในสามเหลี่ยมมุมฉากใดๆ พื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด่านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมของสามเหลี่ยมมุมฉากนั้น " ทฤษฎีบทดังกล่าวสามารถเขียนเป็นสมการสัมพันธ์กับความยาวของด้าน a,b และ c ได้ ซึ่งมักเรียกว่า สมการพีทาโกรัส ซึ่งเขียนเป็นสมการได้ดังนี้ {\displaystyle a^{2}+b^{2}=c^{2}\!\,} (อาจเขียนแทนด้วยตัวแปลอื่น เช่น x,y,z) โดยที่ c เป็นความยาวด้านตรงข้ามมุมฉาก และ a,b เป็นความยาวของอีกสองด้านที่เหลือ ทฤษฎีบทพีทาโกรัสตั้งตามชื่อนักคณิตศาสตร์ชาวกรีก พีทาโกรัส ซึ่งถือว่าเป็นผู้ค้นพบทฤษฎีบทและการพิสูจน์ แม้จะมีการแย้งบ่อยครั้งว่า ทฤษฎีบทดังกล่าวมีมาก่อนหน้าเขาแล้ว มีหลักฐานว่านักคณิตศาสตร์ชาวบาบิโลนเข้าใจสมการดังกล่าว แม้ว่าจะมีหลักฐานหลงเหลืออยู่น้อยมากว่าพวกเขาปรับให้มันพอดีกับกรอบคณิตศาสตร์ ทฤษฎีบทดังกล่าวเกี่ยวข้องกับทั้งพื้นที่และความยาว ทฤษฎีบทดังกล่าวสามารถสรุปได้หลายวิธี รวมทั้งปริภูมิมิติที่สูงขึ้น ไปจนถึงปริภูมิที่มิใช่แบบยูคลิด ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมมุมฉาก และอันที่จริงแล้ว ไปจนถึงวัตถุที่ไม่ใช่สามเหลี่ยมเลยก็มี แต่เป็นทรงตัน n มิติ ทฤษฎีบทพีทาโรัสดึงดูดความสนใจจากนักคณิตศาสตร์เป็นสัญลักษณ์ของความยากจะเข้าใจในคณิตศาสตร์ ความขลังหรือพลังปัญญา มีการอ้างถึงในวัฒนธรรมสมัยนิยมมากมายทั้งในวรรณกรรม ละคร ละครเพลง เพลง สแตมป์และการ์ตูน$

พีทาโกรัสกล่าวว่า ”ผลรวมของ(ด้านประกอบมุมฉากกำลังสอง) = ด้านตรงข้ามมุมฉากกำลังสอง” ซึ่งจากภาพด้านบนก็คือ a2+b2=c2 สมการนี้สมการเดียวเลยน้องที่ต้องจำ! เราเรียกมันว่า สูตรพีทาโกรัส

ตัวอย่างการใช้สมการทฤษฎีบทพีทาโกรัส

ในวิชาคณิตศาสตร์ ทฤษฎีบทพีทาโกรัส แสดงความสัมพันธ์ในเรขาคณิตแบบยุคลิด ระหว่างด้านทั้งสามของสามเหลี่ยมมุมฉาก กำลังสองของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของอีกสองด้านที่เหลือ ในเรื่องของพื้นที่ได้กล่าวไว้ดังนี้ ” ในสามเหลี่ยมมุมฉากใดๆ พื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด่านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมของสามเหลี่ยมมุมฉากนั้น “

ทฤษฎีบทดังกล่าวสามารถเขียนเป็นสมการสัมพันธ์กับความยาวของด้าน a,b และ c ได้ ซึ่งมักเรียกว่า สมการพีทาโกรัส ซึ่งเขียนเป็นสมการได้ดังนี้

ทฤษฎีบทพีทาโกรัส-คณิตศาสตร์ ม.ต้น

ทฤษฎีบทพีทาโกรัส

Author: tmtyai

Related Posts