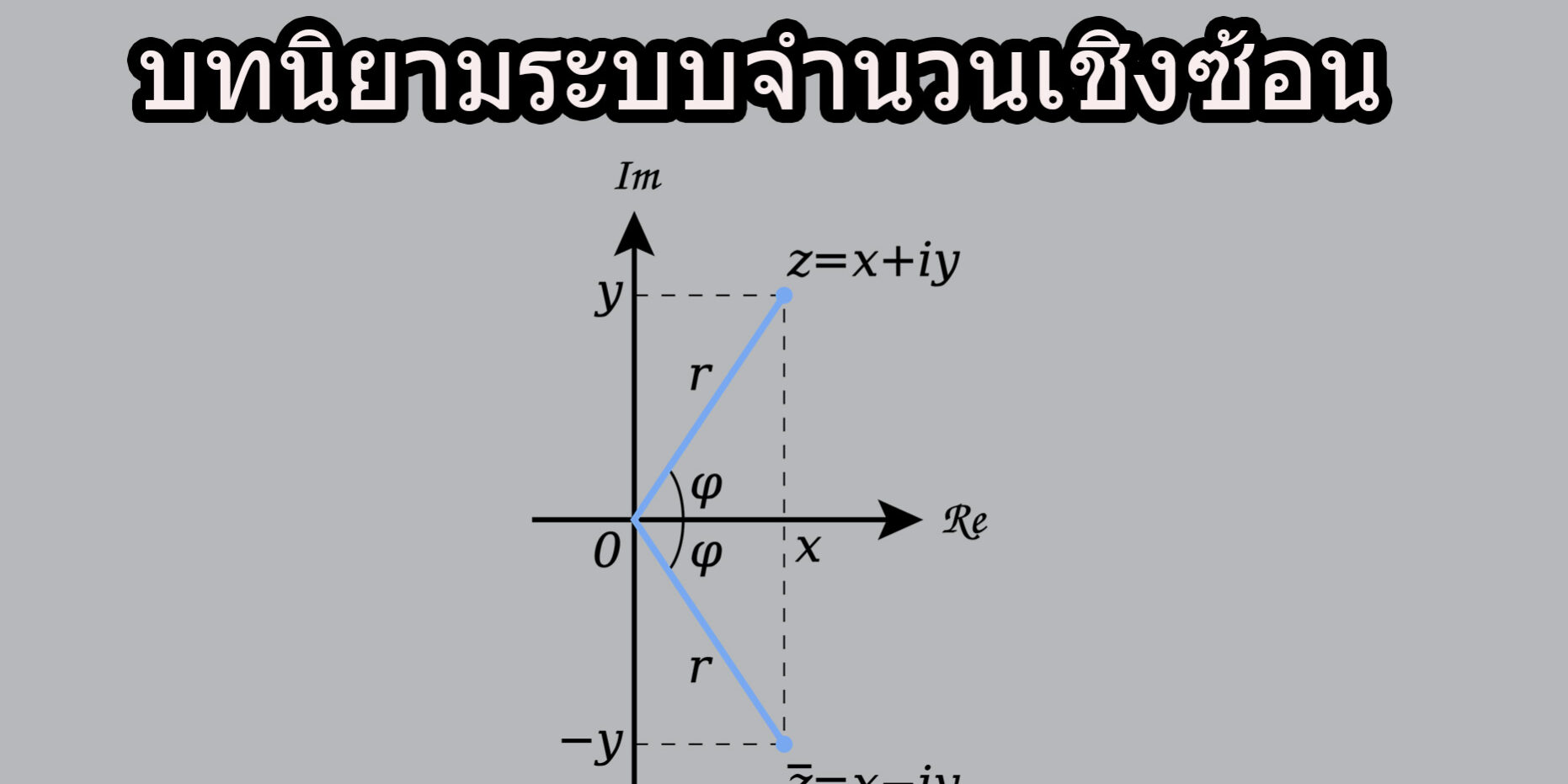
สำหรับจำนวนเชิงซ้อน z = (a, b) เมื่อ a และ b เป็นจำนวนจริง เรียก a ว่าส่วนจริง(real part) ของ z และแทนด้วย Re(z)
เรียก b ว่าส่วนจินตภาพ (imaginary part) ของ z และแทนด้วย Im(z) จะเห็นได้ว่าจำนวนจริงคือจำนวนเชิงซ้อนที่มีส่วนจินตภาพเท่ากับ 0 ซึ่งหมายความว่า เซตของ
จำนวนจริงเป็นสับเซตของจำนวนเชิงซ้อน และจำนวนเชิงซ้อนที่มีส่วนจริงเป็นศูนย์ แต่ส่วนจินตภาพไม่เป็นศูนย์เรียกว่าจำนวนจินตภาพแท้ (purely imaginary number) จำนวนเชิงซ้อน (0, 1) เขียนแทนด้วยสัญลักษณ์ 1 หรือ i ซึ่งเรียก i ว่าหน่วยจินตภาพ(imaginary unit)
| ระบบจำนวนเชิงซ้อน | ||
| นอกจากระบบจำนวนจริงที่กล่าวมาข้างต้นแล้ว ยังมีจำนวนอีกประเภทหนึ่ง ซึ่งได้จากการแก้สมการต่อไปนี้ | ||
| x2 = -1 | ∴ x = √-1 = i | |
| x2 = -2 | ∴ x = √-2 = √2 i | |
| x2 = -3 | ∴ x = √-3 = √3 i | |
| จะเห็นได้ว่า “ไม่สามารถจะหาจำนวนจริงใดที่ยกกำลังสองแล้วมีค่าเป็นลบ” เราเรียก √-1 หรือจำนวนอื่นๆ ในลักษณะนี้ว่า “จำนวนจินตภาพ”และเรียก i ว่า “หนึ่งหน่วยจินตภาพ” เขียนแทนด้วยสัญลักษณ์ i | ||
| ยูเนียนของเซตจำนวนจริงกับเซตจำนวนจินตภาพ คือ ” เซตจำนวนเชิงซ้อน ” (Complex numbers) | ||
บทนิยาม
ถ้า a เป็นจำนวนจริงบวกแล้ว a = a i
บทนิยาม
การบวกจำนวนเชิงซ้อน (a + bi) + (c + di) = (a + c) + (bi + di)
= (a + c) + (b + d)i
การคูนจ ำนวนเชิงซ้อน (a +bi)(c + di) = ac + bci + adi + bdi2
= (ac – bd) + (ad + bc)i
บทนิยาม
ดังนั้น จะได้ตัวผกผัน(อินเวอร์ส) การบวกของ (a, b) คือ (–a, –b)
หรือ ตัวผกผัน(อินเวอร์ส) การบวกของ a + bi คือ –a – bi
ดังนั้น จะได้(1, 0) เป็นเอกลักษณ์การคูณในระบบจำนวนเชิงซ้อน
หรือ 1 + 0i เป็นเป็นเอกลักษณ์การคูณในระบบจำนวนเชิงซ้อน
บทนิยาม (a, b) – (c, d) = (a, b) + (–c, –d)
บทนิยาม ให้ z = a + bi เป็นจำนวนเชิงซ้อน จะเรียกจำนวนเชิงซ้อน a – bi ว่าเป็นสังยุค (conjugate)
ของ z และเขียนแทนด้วยสัญลักษณ์ z นั่นคือ z = a bi = a – bi