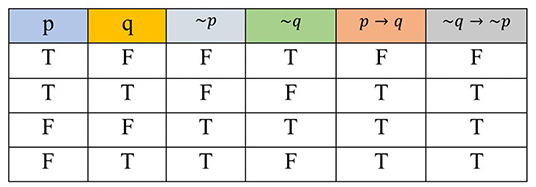
ตัวเชื่อมประพจน์ และค่าความจริงของประพจน์ที่มีตัวเชื่อม
“และ” “หรือ” “ไม่” ที่เหลืออีกสองตัวคือ “ถ้า…แล้ว…” และ “…ก็ต่อเมื่อ…” เมื่อนำประพจน์เชื่อมด้วยตัวเชื่อม และ ,หรือ, ถ้า…แล้ว, …ก็ต่อเมื่อ
โดยที่ถ้า p และ q แทนประพจน์ จะเขียน
ถ้ากำหนดให้ T แทนค่าความจริงของประพจน์ที่เป็นจริง
F แทนค่าความจริงของประพจน์ที่เป็นเท็จ
และ p, q แทนประพจน์ใดๆ ที่ยังไม่ได้ระบุข้อความหรือแทนค่าข้อความลงไป
ประพจน์ p ู q จะเรียกว่าข้อความร่วม (conjugate statement) และจะสามารถเขียนตารางค่าความจริงของประพจน์ p ู q ได้ดังนี้
และ (∧)
และ เป็นตัวเชื่อมประพจน์ที่บอกว่าประพจน์จะมีค่าความจริงเป็นจริงเมื่อประพจน์ย่อยทั้งสองประพจน์มีค่าความจริงเป็นจริงเท่านั้น ตารางค่าความจริงของ ‘และ’ คือ
| pp | p∧qp∧q | |
|---|---|---|
| TT | TT | TT |
| TT | FF | FF |
| FF | TT | FF |
| FF | FF | FF |
จากตารางจะพบว่า ค่าความจริงของประพจน์ p ู q จะเป็นจริงถ้าประพจน์ทั้งสองเป็นจริงนอกนั้นจะเป็นเท็จ
ประพจน์ p ฺ q เรียกว่าข้อความเลือก (disjunctive statement) เป็นข้อความที่เป็นจริงถ้า p หรือ q เป็นอย่างน้อยที่สุดหนึ่งประพจน์ แต่จะไม่เป็นจริงเมื่อทั้งสองประพจน์เป็นเท็จ ตารางค่าความจริงของ p ฺ q สามารถเขียนได้ดังนี้
หรือ (∨)
หรือ เป็นตัวเชื่อมประพจน์ที่บอกว่า ถ้ามีประพจน์ย่อยใดประพจน์นึงมีค่าความจริงเป็นจริงจะได้ว่าประพจน์นั้นมีค่าความจริงเป็นจริง ตารางค่าความจริงของ ‘หรือ’ คือ
| pp | p∨qp∨q | |
|---|---|---|
| TT | TT | TT |
| TT | FF | TT |
| FF | TT | TT |
| FF | FF | FF |
หรือ (∨)(∨) จะให้ค่าความจริงเป็น เท็จกรณีเดียว เท่านั้น คือ F∨FF∨F
นิเสธ (∼)
นิเสธ คือ การที่เราจะเอาค่าความจริงที่อยู่ตรงข้ามกับค่าความจริงของประพจน์นั้น ตารางค่าความจริงของ ‘นิเสธ’ คือ
| pp | ∼p∼p |
|---|---|
| TT | FF |
| FF | TT |
เช่น p : นุ่นไปเที่ยวนอกบ้าน
q : คุณพ่อโทรศัพท์ตาม
ดังนั้น p ,q : ถ้านุ่นไปเที่ยวนอกบ้านแล้วคุณพ่อโทรศัพท์ตาม
จากการตรวจสอบเงื่อนไขนี้จะพบว่าประพจน์นี้จะเป็นเท็จกรณีเดียวคือ นุ่นไปเที่ยวนอกบ้านแต่คุณพ่อไม่โทรศัพท์ตาม ดังนั้นจะสามารถแสดงตารางค่าความจริงของประพจน์ p , q ได้ดังนี้
ถ้าแล้ว (→)
ถ้าแล้ว เป็นตัวเชื่อมที่ประพจน์ที่อยู่หน้าเครื่องหมายถ้าแล้ว จะเป็นเหตุ และ ประพจน์ที่อยู่หลังเครื่องหมายถ้าแล้วจะเป็นผล
ตารางค่าความจริงของ ‘ถ้าแล้ว’ คือ
| pp | p→qp→q | |
|---|---|---|
| TT | TT | TT |
| TT | FF | FF |
| FF | TT | TT |
| FF | FF | TT |
ถ้าแล้ว (→)(→) จะมีค่าความจริงเป็น เท็จกรณีเดียว เท่านั้น คือ T→FT→F
ก็ต่อเมื่อ (↔)
ก็ต่อเมื่อ เป็นตัวเชื่อมที่จะให้ค่าความจริงเป็นเมื่อทั้งสองประพจน์ที่เชื่อมมีค่าความจริงเหมือนกัน ตารางค่าความจริงของ ‘ก็ต่อเมื่อ’ คือ
| pp | p↔qp↔q | |
|---|---|---|
| TT | TT | TT |
| TT | FF | FF |
| FF | TT | FF |
| FF | FF | TT |
จากตารางค่าความจริงของประพจน์ที่มีตัวเชื่อมทั้ง 5จะพบว่า
1. ~ p มีค่าความจริงตรงกันข้ามกับค่าความเป็นจริงของ p
2. p ,q เป็น T กรณีเดียวคือกรณีที่ทั้ง p และ q เป็น T
3. p ,q เป็น F กรณีเดียวคือกรณีที่ทั้ง p และ q เป็น F
4. p , q เป็น F กรณีเดียวคือกรณีที่ทั้ง p เป็น T และ q เป็น F
5. p ,q เป็น T เมื่อ p และ q มีค่าความจริงเหมือนกัน