ในเรื่องจำนวนนับมีเรื่องที่สำคัญที่ต้องกล่าวถึงอีกคือ จำนวนนับจำแนกได้อีก 2 ประเภท คือ จำนวนคู่และจำนวนคี่ ซึ่งมีรายละเอียดดังนี้

        1. จำนวนคู่ (Odd Number) คือจำนวนนับที่ 2 หารได้ลงตัว เช่น 2,4,6,…

        2. จำนวนคี่ (Even Number) คือจำนวนนับที่ 2 หารแล้วเหลือเศษ เช่น 1,3,5,…

        จากที่กล่าวมาจะยกตัวอย่างตัวเลขเพื่อแสดงว่าจำนวนใดเป็นจำนวนคู่หหรือจำนวนคี่ ดังนี้

        10      เป็นจำนวนคู่ เพราะ 10   หาร 2 = 5

        46      เป็นจำนวนคู่ เพราะ 46   หาร 2 = 23

        121    เป็นจำนวนคู่ เพราะ 121 หาร 2 ได้ 60 เศษ 1

        เมื่อนำจำนวนคู่หรือจำนวนคี่ มาบวกหรือคูณกันจะได้เป็นจำนวนคู่หรือจำนวนคี่นั้นมีข้อสังเกตบางประการของการบวกและการคูณจำนวนคู่หรือจำนวนคี่ ดังนี้

        การบวก

        – จำนวนคู่ + จำนวนคี่ จะได้ จำนวนคู่

                เช่น 2+6 = 8,4+8 = 12

        – จำนวนคู่ + จำนวนคี่ จะได้ จำนวนคี่

                เช่น 2+3 = 5,4+5 = 9

        – จำนวนคี่ + จำนวนคี่ จะได้ จำนวนคู่

                เช่น 1+1 = 2,3+5 = 8

        การคูณ

        – จำนวนคู่ + จำนวนคี่ จะได้ จำนวนคู่

                เช่น 2 = 8,4+8 = 12

        – จำนวนคู่ + จำนวนคี่ จะได้ จำนวนคู่

                เช่น 2+3 = 5,4+5 = 9

        – จำนวนคี่ + จำนวนคี่ จะได้ จำนวนคี่

                เช่น 1+1 = 2,3+5 = 8

            (2) จำนวนเต็มลบ (Negative Integers) เป็นจำนวนที่ใช้แทนปริมาณที่น้อยกว่าศูนย์ เขียนแทนด้วยเลขจำนวนนับที่มีเครื่องหมายลบอยู่ด้านหน้า โดยจำนวนเต็มลบเริ่มจาก –1 และลดลงทีละ 1 ไปเรื่อยๆไม่มีที่สิ้นสุด เช่น –2,-3,-5,… เป็นต้น

     2. จำนวนเศษส่วน (Fractions) เป็นจำนวนที่สร้างขึ้นเพื่อใช้แทนจำนวนที่ไม่ใช่จำนวนเต็ม โดยทั่วไปเศษส่วนใดๆเขียนได้ในรูป a/b โดย a,b เป็นจำนวนเต็ม และ b ≠ 0 เรียก a ว่าตัวเศษ (Numerator) หมายถึง จำนวนส่วนแบ่งที่ต้องการ และ b ว่า ตัวส่วน (Denominator) หมายถึง จำนวนทั้งหมดที่มีอยู่เช่น 1/3 เรียก 1 ว่าเศษ และเรียก 3 ว่าส่วน หมายถึง มีของอยู่ทั้งหมด 3 ส่วนต้องการเพียง 1 ส่วน เพื่อแสดงจำนวนเศษส่วนให้เห็นชัดเจนขึ้น จึงนำไปเขียนแสดงบนเส้นจำนวนโดยใน 1 หน่วย ความยาวบนเส้นจำนวน จะแบ่งความยาวออกเป็นส่วนๆที่เท่าๆกัน ดังรูปที่ 1.5

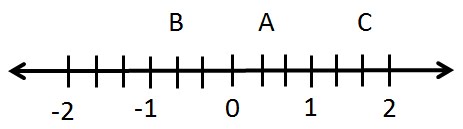
                                                                                                        รูปที่ 1.5 เส้นจำนวนแสดงจำนวนเศษส่วน

            จากรูปที่ 1.5 อธิบายได้ว่า เส้นจำนวนแบ่งระยะห่างออกเป็น 3 ส่วนเท่าๆกัน จุด A,B,C มีความหมายดังนี้

            จุด A แทน 1/3 แสดงว่าจุด A อยู่ห่างจาก 0 ไปทางขวามือเป็นระยะทาง 1 ส่วนของทั้งหมด 3 ส่วน

            จุด B แทน –2/3 แสดงว่าจุด B อยู่ห่างจาก 0 ไปทางซ้ายมือเป็นระยะทาง 2 ส่วนของทั้งหมด 3 ส่วน

            จุด C แทน 5/3 แสดงว่าจุด C อยู่ห่างจาก 0 ไปทางขวามือเป็นระยะทาง 5 ส่วนของทั้งหมด 3 ส่วน

            เศษส่วนสามารถแบ่งออกได้เป็น 3 ประเภท ดังนี้

1. เศษส่วนแท้ คือ เศษส่วนที่มีค่าน้อยกว่า 1 หรือตัวเศษมีค่าน้อยกว่าตัวส่วน เช่น 1/4,3/5

2. เศษส่วนเกิน คือ เศษส่วนที่มีค่ามากกว่า 1 หรือตัวเศษมีค่ามากกว่าตัวส่วน เช่น 3/2,5/3

3. เศษส่วนจำนวนคละ คือ เศษส่วนที่มีจำนวนเต็มส่วนหนึ่งกับเศษส่วนของจำนวนเต็มอีกส่วนหนึ่ง

        ข้อสังเกต ของจำนวนเศษส่วน

จำนวนเต็มทุกจำนวนสามารถเขียนให้อยู่ในรูปเศษส่วนได้ คือ ส่วนเป็น 1 เสมอ แต่ไม่นิยมเขียน 1 กำกับไว้

สามารถเปลี่ยนจำนวนที่อยู่ในรูปเศษส่วนให้เป็นทศนิยมได้โดยนำตัวส่วนไปเป็นตัวหารเศษ

กรณี 2/9 = 0.222… เมื่อหารไปเรื่อยๆจะได้เลข 2 ซ้ำกันเพราะหารเหลือเศษเท่ากันทุกครั้ง ทศนิยมที่ได้นี้เรียกว่า ทศนิยมซ้ำ เช่น 1/15 = 0.0666… หรือ 0.06 อ่านว่า ศูนย์จุดศูนย์หก หกซ้ำ , 5/6 = 0.8333… หรือ 0.83 อ่านว่า ศูนย์จุดแปดสาม สามซ้ำ , 3/4 = 0.75 หรือ 0.750 อ่านว่าศูนย์จุดเจ็ดห้าศูนย์ ศูนย์ซ้ำ เพราะเมื่อหารไปเรื่อยๆจะได้ศูนย์ซ้ำ แต่จะไม่นิยมเขียนศูนย์ซ้ำ ดังนั้นเศษส่วนทุกจำนวนสามารถเปลี่ยนเป็นรูปทศนิยมซ้ำได้

         3. จำนวนทศนิยม (Decimal Numbers) เป็นจำนวนที่ประกอบไปด้วย 2 ส่วน คือ ส่วนที่เป็นจำนวนเต็มและส่วนที่เป็นทศนิยม และใช้สัญลักษณ์จุด (.) คั่นระหว่างส่วนที่เป็นจำนวนเต็มและส่วนที่เป็นทศนิยมหรือการเขียนตัวเลขแสดงจำนวนที่มีค่าน้อยกว่า 1

            จำนวนทศนิยมที่เป็นจำนวนตรรกยะสามารถแบ่งได้เป็น 2 ประเภท คือ

            (1) ทศนิยมรู้จบ เป็นจำนวนที่มีตัวเลขหลังจุดทศนิยมแน่นอนหรือมีศูนย์ซ้ำ เช่น 1.2, 3.55, 9.245 เป็นต้น

            (2) ทศนิยมไม่รู้จบชนิดซ้ำกัน  เป็นจำนวนที่มีเลขทศนิยมตัวหนึ่งหรือมากกว่าซ้ำๆกันไม่มีที่สิ้นสุด โดยคาดเดาเลขทศนิยมตัวตต่อไปได้ว่าจะเป็นเลขอะไร เช่น 0.23, 1.54, 40.64 เป็นต้น

            1.1.2 จำนวนอตรรกยะ

                      จำนวนอตรรกยะ (Irrational Numbers) คือ จำนวนที่ไม่สามารถเขียนในรูปเศษส่วนของจำนวนเต็มที่ตัวหารไม่เป็นศูนย์ แต่เขียนได้ในรูปทศนิยมไม่ซ้ำและสามารถกำหนดค่าโดยประมาณได้

            จำนวนอตรรกยะสามารถแบ่งได้ เป็น 3 ประเภท คือ

            1. จำนวนที่อยู่ในเครื่องหมายกรณฑ์ () และไม่สามารถถอดค่าออกมาได้เป็นตัวเลขที่แน่นอน เช่น = 1.73205080757……. เป็นต้น

            2. จำนวนทศนิยมไม่รู้จบและไม่ซ้ำกัน ได้แก่ ทศนิยมที่มีตัวเลขหลังจุดทศนิยมมากมายโดยไม่ซ้ำกันและไม่สามารถคาดเดาตัวเลขตัวต่อไปได้เลยว่าเป็นเลขอะไร เช่น 0.5836…, 1.2573…, 3.4925… เป็นต้น

            3. ค่า และ e โดย เป็นค่าคงตัวทางคณิตศาสตร์ที่เกิดจากความยาวเส้นรอบวงหารด้วยเส้นผ่านศูนย์กลางของวงกลม ค่าของ = 3.14159265359… และ e เป็นตัวเลขของออยเลอร์ (Euler Number หรือ Eulerian Number) ค่าของ e = 2.71828182846…

ห.ร.ม.และ ค.ร.น.

ความสัมพันธ์ ห.ร.ม. กับ ค.ร.น.