ผลบวกของอนุกรมอนันต์  การหาผลบวกของอนุกรมอนันต์นั้นจะอาศัยความรู้เรื่องลิมิตมาช่วยในการหาผลบวกครับ ซึ่งเราไปดูพวกนิยามต่างๆที่สำคัญเกี่ยวกับการหาผลบวกของอนุกรมอนันต์

บทนิยาม 

กำหนดให้  a₁ + a₂ + a₃ + a₄ + a₅  +⋯+a_ืn+⋯ เป็นอนุกรมอนันต์

อนุกรมอนันต์

อนุกรมอนันต์  [Infinite Series]
นิยาม   อนุกรมอนันต์ คือ อนุกรมที่มีจำนวนพจน์ไม่จำกัด    ;    a₁ + a₂ + a₃ + … + a_n + …
ถ้า

s₁             =             a₁
s₂             =             a₁ + a₂
s₃             =             a₁ + a₂ + a₃

:

:

s_n             =             a₁ + a₂ + a₃ + … + a_n

แล้ว   s_{1 ,} s₂ , s₃ , … , s_n  แต่ละจำนวนเราเรียกว่า “ ผลบวกย่อย “ [ Partial Sum ]  ของอนุกรม  a₁ + a₂ + a₃ + … + a_n + …  และ  เรียก  s_{1 ,} s₂ , s₃ , … , s_n ว่า “ ลำดับผลบวกย่อยของอนุกรม “

ถ้าลำดับผลบวกย่อยของอนุกรมมีลิมิต  [ lim S_n  =  L ]  แสดงว่า  อนุกรมนี้หาผลบวกได้
ซึ่งผลบวกของอนุกรมอนันต์จะเท่ากับ  L  และเรียกอนุกรมนี้ว่า “ อนุกรมคอนเวอร์เจนต์ “

ถ้าลำดับผลบวกย่อยของอนุกรมหาลิมิตไม่ได้   แสดงว่า  อนุกรมนี้หาผลบวกไม่ได้
เราเรียกอนุกรมแบบนี้ว่า “ อนุกรมไดเวอร์เจนต์ “

ข้อสังเกต      ผลบวกอนันต์ของอนุกรม  ก็คือ  ลิมิตของลำดับผลบวกย่อยของอนุกรมนั้นเอง

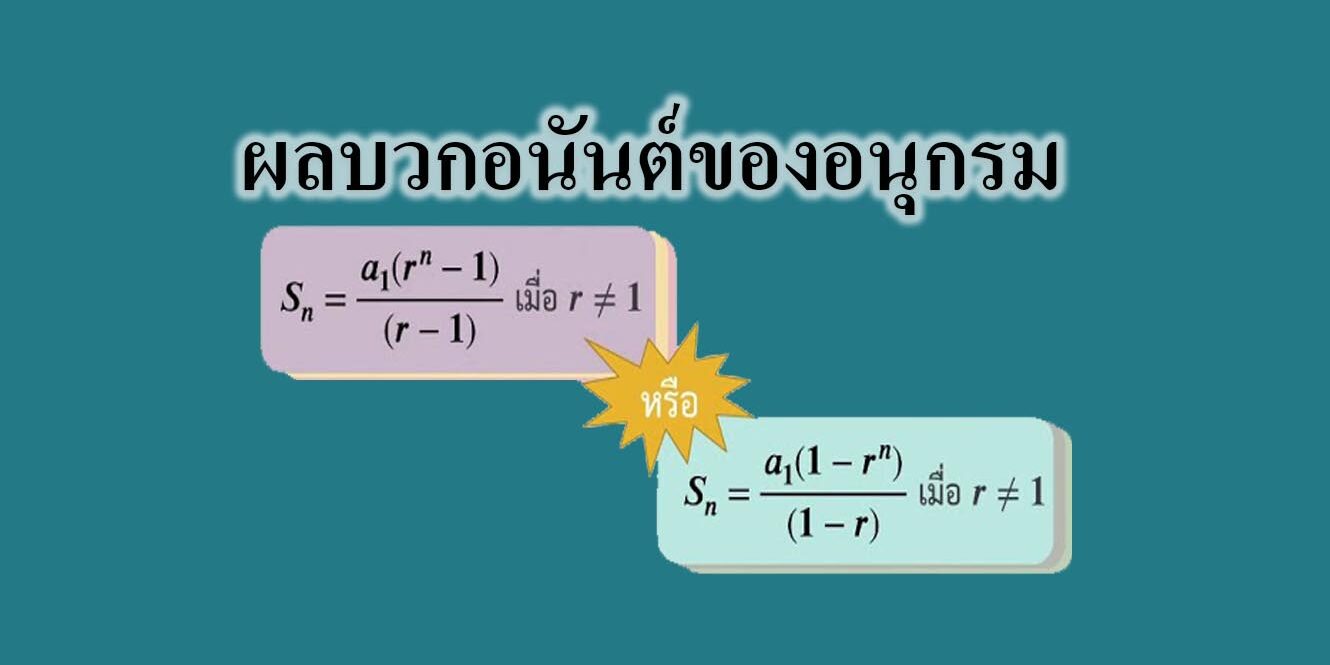
 การหาผลบวกอนันต์ของอนุกรมเรขาคณิต

เรียก SnSn ว่า ผลบวกย่อย (partialsum)(partialsum) n พจน์แรกของอนุกรม เมื่อ nn เป็นจำนวนเต็มบวก

เรียกลำดับอนันต์ S1,S2,S3,⋯,Sn,⋯S1,S2,S3,⋯,Sn,⋯ ว่าลำดับของผลบวกย่อยของอนุกรม

ไปดูอีกนิยาม ครับ อ่านนิยามให้เข้าใจแล้วลองทำแบบฝึกหัดครับ

บทนิยาม

กำหนดอนุกรมอนันต์ a₁ + a₂ + a₃ + … + a_n + …

ให้ S₁ ,S₂ ,⋯,S_n ,⋯S₁ ,S₂ ,⋯,S_n ,⋯ เป็นลำดับของผลบวกย่อยของอนุกรมนี้ ถ้าลำดับ SnSn เป็นลำดับลู่เข้า โดย limn→∞ S_n =S lim n→∞S_n =S เมื่อ SS เป็นจำนวนจริงแล้วจะกล่าวว่าอนุกรม a₁ + a₂ + a₃ + … + a_n + …  เป็นอนุกรมลู่เข้า (covergent  series) และเรียก SS ว่าผลบวกของอนุกรม

ถ้าลำดับ S_n เป็นลำดับลู่ออก จะกล่าวว่าอนุกรม  a₁ + a₂ + a₃ + … + a_n + … เป็นอนุกรมลู่ออก (divergent series)

สรุปนะคับ  จากนิยาม การหาผลบวกของอนุกรมอนันต์สามาทำได้ 2 ขั้นตอนคือ

1. หาสูตรทั่วไปของผลบวกย่อย n  พจน์แรก หรือก็คือ หาสูตรทั่วไปของ S_n  นั่นเองครับ

2   นำค่า S_n  จากข้อ 1. มาหาค่าลิมิต ลิมิตที่ได้นั้นจะเป็นคำตอบของอนุกรมอนันต์  และอนุกรมอนันต์เป็นอนุกรมลู่เข้า

ลําดับเลขคณิต 

• ลำดับเลขคณิต : ขวา-ซ้าย คงที่
• พจน์ทั่วไป คือ a₁ + (n-1)d
•  a_m    =  a_n + (m-n)d

เทคนิคการทำโจทย์ เมื่อโจทย์ให้ผลบวกของลำดับเลขคณิตโดย

จำนวนพจน์เป็นเลขคี่
a₁ + a₂ + a₃ + a₄ + a₅
a₁  = x – 2d
a₂  =   x – d
a₃  =  x
a₄   =  x + d
a₅   =  X + 2d

จำนวนพจน์เป็นเลขคู่
a₁ + a₂ + a₃ + a₄
a₁  = x – 3d
a₂  =   x – d
a₃  =  x+d
a₄   =  x + 3d

บทนิยาม   อนุกรมเลขคณิต

อนุกรมที่ได้จากลำดับเลขคณิต เรียกว่า อนุกรมเลขคณิต และผลต่างร่วมของลำดับเลขคณิต เป็นผลต่างร่วมของอนุกรมเลขคณิตด้วย

เมื่อ a₁ , a₁ + d, a₁ + 2d, …, a₁  + (n – 1)d เป็นลำดับเลขคณิต

จะได้ a₁  + (a₁  + d) + (a₁  + 2d) + … + (a₁  + (n – 1)d) เป็นอนุกรมเลขคณิต

ซึ่งมี a₁  เป็นพจน์แรกของอนุกรม และ d เป็นผลต่างร่วมของอนุกรมเลขคณิต

จากบทนิยาม จะได้ว่า ถ้า a₁ ,a₂ ,a₃ , …,a_n เป็น ลำดับเลขคณิต ที่มี n พจน์

จะเรียกการเขียนแสดงผลบวกของพจน์ทุกพจน์ของลำดับในรูป

a₁ + a₂ + a₃+ … + a_nว่า อนุกรมเลขคณิต

และผลต่างร่วม ( d ) ของลำดับเลขคณิต เป็นผลต่างร่วมของอนุกรมเลขคณิตด้วย

ตัวอย่างของอนุกรมเลขคณิต

3. 1 + 3 + 5 + 7 + … + 99 เป็น อนุกรมเลขคณิต

เพราะว่า 1, 3, 5, …, 99 เป็น ลำดับเลขคณิต และมีผลต่างร่วมเท่ากับ 2

 

4. 25 + 20 + 15 + 10 + … เป็น อนุกรมเลขคณิต

เพราะว่า 25, 20, 15, 10, … เป็น ลำดับเลขคณิต และมีผลต่างร่วมเท่ากับ – 5

 

5. 7 + 14 + 21 + 28 + … เป็น อนุกรมเลขคณิต

เพราะว่า 7, 14, 21, 28, … เป็น ลำดับเลขคณิต และมีผลต่างร่วมเท่ากับ 7